| |
E.
De totius identitatis et oppositionis figura.
I.
Totius identitatis et oppositionis figura aequidistantibus
et secantibus lineis absolvitur.
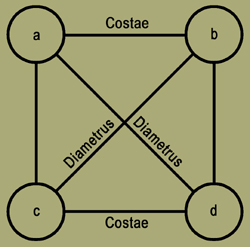
(1) Identitas et oppositio simul sunt tota duorum oppositorum ratio et comparatio, quam quadratura absolvi diximus. Duae quipppe habitudines gignuntur utriusque in se ipsum flexura. Duae vero utriusque in alterutrum transitione et emigratione. Et has eorum collationes prius trinis orbibus expressimus. Extremi enim orbes designabant utriusque in se ipso mansionem ac statum. Medius vero orbis amborum commeatum ostendebat. Nunc autem aliter pingi volumus oppositionum quadraturam, id est eorum identitatem et oppositionem sive habitudines quattuor, per rectas, inquam, lineas sive per quadrati costas atque diametros. Sunt enim hae duae se secantes, illae vero aequidistantes.
II.
Totius quadrati costae identitatem,
diametri vero oppositionem designant.
(2) Nam costae quadrati sunt aequidistantes statuentes quodlibet in se ipso. Diametri vero mutua sectione in angulos procedunt statuentes aut utrumque oppositum extra se ipsum aut utraque in eodem, quae sunt praeter naturam.
III.
Unde manifestum est extremas oppositorum comparationes eorum
esse identitatem, medias vero eorum oppositionem.
(3) Nam costae quadrati extremae sunt eius lineae, diametri vero mediae eiusdem lineae. Costae insuper sunt lineae simplicitatis, absolutionis, impermixtionis et proprietatis omnium. Diametri vero lineae sunt contractionis, permixtionis et communitatis. Omnia secundum costas sunt absoluta, impermixta, propria et incommunicata. Per diametros vero aut angulos ab sua sede singula emigrant, permiscentur et communicantur. Et eodem modo hac figura ad cuncta opposita poteris uti et ex ea inferre, quaecumque secundum uniuscuiusque rei naturam aut contra naturam sunt.
IV.
In eadem figura duo semper ut subiecta,
duo vero ut praedicata et attributa sumenda sunt.
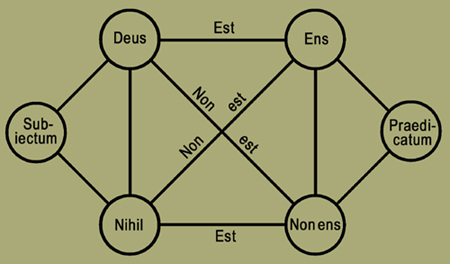
(4) Aut enim praedicas atque enuntias utrumque oppositum de se ipso aut eius locum aut rationem aut aliud quippiam. Itaque ipsa imprimis duo opposita, quibus aliquid tribuis, statuenda abs te sunt ut supposita et subiecta contra se invicem. Quae vero de ipsis enuntias, sub ipsis sunt ex opposito collocanda. Et nihil refert sine subiecta utraque colloces in parte superiore et eorum attributa in inferiore. Aut subiecta in latere sinistro, attributa vero in dextro. Hic tamen faciendae oppositorum figurae modus priore erit commodior. Verbi gratia deus et nihil subiecta quaedam sunt; eorum vero praedicata esse et non esse sive ens et non ens. Statue igitur deum et nihil ut subiecta sinistro in latere! Ens vero et non ens ut eorum praedicata in dextro atque hoc modo omnium oppositorum amplissimae utilitatis figuram complebis.
V.
Oppositorum identitas est rarior,
oppositio vero plurior et multiplicior.
(5) Nam tantum duae costae, quae de utroque subiecto proprium attributum dicunt atque enuntiant, eorum exprimunt identitatem. Utraque vero diametrus eorum infert oppositionem. Et quomodocumque costam cum diametro sumpseris, iterum oppositionem concludis, ut si idem de utroque subiecto pronuntias, quod bis contingit, aut si rursum de eodem subdito gemina infers attributa, quod iterum bis fieri potest.
VI.
Identitates sunt tantum duae,
oppositiones vero numero sex.
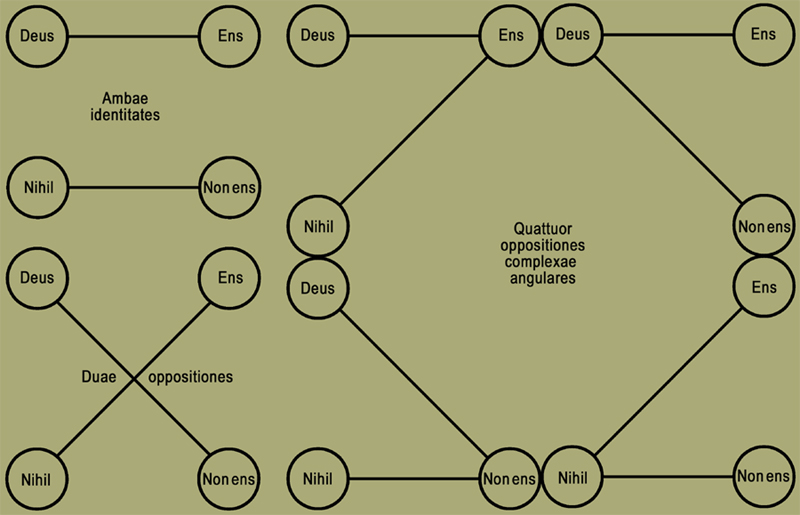
(6) Diximus in praecedente tantum duas esse identitates, eas, inquam, quadrati costas, quae subditis copulant praedicata. Nam ceterae duae costae, quae inter ambo subiecta et inter ambo praedicata protenduntur, neque identitatis neque oppositionis nomine censentur, quod secundum ipsas nulla fiat enuntiatio. Haud enim subiectum de subiecto neque de praedicato praedicatum enuntiatur ac dicitur. Cetera vero eorum omnis comparatio est oppositio. Nam utraque diametrus est oppositio, utpote quae utrique subiecto contrarium tribuit praedicatum. Superant et aliae oppositiones quattuor, sed complexae et angulares constantes ex diametro et costa, quibus aut utrique subiecto ut deo et nihilo tantum unum tribuis praedicatum ut utrique ens aut utrique non ens. Aut quibus de eodem subiecto utrumque simul enuntias praedicatum ut de deo ens et non ens aut de nihilo ens et non ens.
VII.
Sex oppositionum tantum duae simplices et lineares sunt,
ceterae vero complexae atque angulares.
(7) Duae oppositiones simplices sunt utraque diametrus; quae tantum unum de tantum uno, incommode et contrarie enuntiant, ut de deo non ens et de nihilo ens. Ceterae vero quattuor oppositiones sunt complexae et angulares; unaquaeque enim earum duabus constat lineis, diametro et costa; hae autem angulum claudunt enuntiantque contra naturam de uno duo aut de duobus unum.
VIII.
Identitas est simplici oppositioni aequalis.
(8) Nam identitas oppositorum sunt lineae tantum duae, sed aequidistantes, ut quadrati costae. Simplex vero oppositio duae itidem lineae sunt, sed intersectae, ut utraque diametrus. Et rursum simplex oppositio est quattuor rectorum angulorum spatium sive quattuor recti anguli, qui diametrorum mutua sectione perficiuntur. Identitas autem simplex est et quattuor rectorum spatium, quod inter aequidistantes iacet intercipiturque. Utraque enim aequidistantium duorum rectorum spatium complectitur. Simplex igitur identitas simplici oppositioni et linearum numero et angulorum spatio atque intercapedine aequa relinquitur.
IX.
Rursum utraque simplex et identitas et oppositio, singulae per se,
cunctis complexis oppositionibus sunt duplae.
(9) Nam utraque simplex et identitas et oppositio per se est ut quattuor recti anguli. Unaquaeque autem complexa oppositio est per se ut unius recti medietas. Omnes vero simul ut duo recti. Quattuor autem recti ad rectos duos sunt dupli. Est igitur simplex identitas ad cunctas oppositiones complexas dupla. Similiter et simplex oppositio ad easdem dupla.
X.
Universa oppositorum figura quaternarii quadrato rectos angulos involvit
completque rectorum angulorum quadraturam.
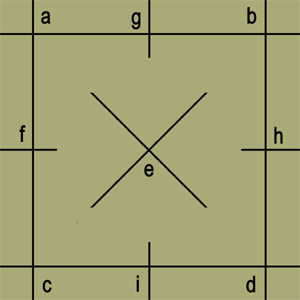
(10) Quaternarii quadratus est decimus sextus, quem dicimus esse mensuram rectorum angulorum, qui quadrate insunt oppositorum figurae. Nam insunt imprimis quadrato recti anguli, quattuor extremi et angulares. Deinde protractis in eodem ambabus diametris fiunt alii recti quattuor ad quadrati centrum diametrorum sectione. Et unaquaeque quadrati costa intra quadratum claudit super se duorum rectorum spatium. Quod liquidius intueberis, si costas omnes secueris medias per duas rectas ad costas aequidistantes. Universa igitur interior quadrati superficies (quam oppositorum figuram nuncupamus) quaternarii quadrato, id est decimo sexto numero rectos angulos claudit completque rectorum angulorum quadraturam. Quodsi in quadrato lineas omnes ad sectionem extra quadratum produxeris, complebuntur omnes anguli recti tam introrsus quam extrorsus senarii quadrato, id est sexto et tricesimo numero. Intra enim quadratum clauduntur recti anguli sedecim. Ex vicesimo autem et sexto decimo sextus et tricesimus senarii quadratus conflatur. Sit enim quadratus a b c d, cuius centrum e. Protendo ambas ipsius diametros a e d et b e c, quarum sectio super centrum e erit quattuor rectorum angulorum creatio. Partior deinde quamlibet eius costam per medium punctis f g h i et produco lineas f e h et g e i intra et extra quadratum. Extendo insuper singulas costas in utramque partem ultra quadratum. Manifestum est in toto quadrato signata esse puncta novem, scilicet a f c g e i et b h d et circa unumquodque eorum tam extra quam infra quadratum factos esse rectos quattuor. Nam circa lineam a f c facti sunt recti duodecim. Circa lineam g e i recti duodecim. Ad lineam quoque b h d recti duodecim, qui simul sex et triginta rectorum summam implent. Et horum sedecim sunt intra quadratum: quattuor scilicet ad centrum, octo ad medias costas et ad praecipuos angulos quattuor. Viginti vero extra quadratum relinquuntur. Ad medias costas octo et ad quattuor angulos duodecim. Quippe circa unumquemque capitalem praecipuumve totius quadrati angulum sunt extra quadratum tres rectae. Absolvitur igitur universa oppositorum figura tam foris quam intus rectis angulis sex et triginta.
|