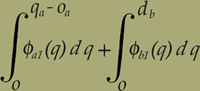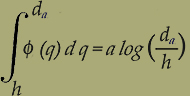Considerazioni sui principii fondamentali

dell'economia politica pura

1892

______________________________________________________________________________

[405]

II.

Il valore.

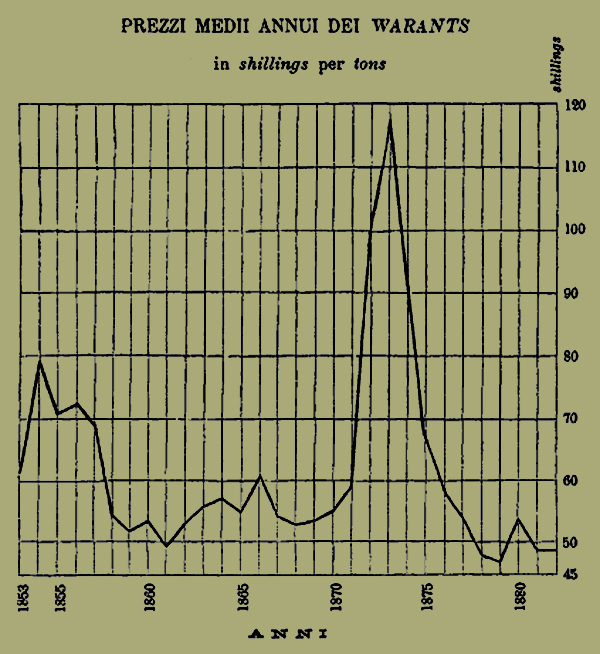
Oggetto di una teoria del valore. I fatti reali che noi possiamo osservare sono le vendite di alcune merci che si [406] pagano certi prezzi. Oggetto di una teoria di valore non può essere che di spiegare quei fatti, collegarli, e farli apparire quali conseguenza di uno o di pochi principii.

La via empirica sarebbe quella che porterebbe a raccogliere molte notizie sui prezzi, riunirle insieme e vedere se se ne può ricavare qualche legge. Consentiamo che con questo metodo, che il Mill chiama chimico ¹⁾, non si può giungere a nessuna legge veramente razionale, mentre è pure sempre molto utile avere tali notizie e le leggi empiriche che possono giovare come un primo passo nella ricerca della verità.

Il metodo geometrico od astratto ²⁾ non si cura di quei fatti; stabilisce certi assiomi sull'indole degli uomini, e deduce come deve seguire il fenomeno del valore. Neppure per questa via crediamo che si possa giungere a conoscere la verità, anzi la reputiamo più fallace della precedente.

Finalmente il metodo «deduttivo concreto» assume certa ipotesi per provare se sono vere o no. Con questo intento ne deduce le leggi del valore, le quali poscia paragona coi fatti naturali, e secondochè concordano o discordano, accetta, o modifica, o interamente rigetta lo ipotesi.

Sinchè stiamo sulle generali nessuno forse si opporrà a questo considerazioni, che, per essere ben note, saranno anzi stimate qui superflue. Ma scendendo ai particolari la cosa non correrà più tanto piana, e facilmente si useranno quei ragionamenti che prima, in massima, si sarebbero esclusi. Vi è una certa tendenza nella nuova scuola a sottomettere l'esperienza alle sue teorie, ed in ciò forse sta il maggiore pericolo per essa; onde è bene procurare in ogni modo di scansarlo.

Ragioneremo meglio sovra un esempio concreto. Il diagramma qui sotto ci mostra i prezzi della ghisa (warants) e Glasgow per molti anni. [407]

Una teoria perfetta del valore sarebbe quella, la quale, conosciute tutte le circostanze del mercato, esclusi i soli prezzi della ghisa, ci permetterebbe di calcolare quei prezzi in modo da riprodurre precisamente quel diagramma.

★ Non altrimenti ha dovuto operare l'astronomia per salire al grado di perfezione, al quale è giunta ai tempi nostri. Senza il Keplero, od alcun altro che avesse compiuto il lavoro da lui fatto, l'astronomia non esisterebbe. Il diagramma dei prezzi, che abbiamo segnato pare, ed è, assai irregolare, ma anche la curva descritta da Marte non era facile a conoscersi. Veggasi nelle opere del Keplero la viva descrizione che fa delle fatiche da lui durate. «Mentre con questo mezzo trionfo dei movimenti di Marte, e che, credendolo vinto, preparo specchi ed equazioni per imprigionarlo, [408] mi si annunzia che è altrove. Vana vittoria! Devesi tornare a principiare il terribile combattimento; giacché l'innemico tenuto da me prigione, incatenato come un prigioniero che sì trascura, ha spezzate le ritorte delle equazioni, ed è fuggito dai miei specchi numerici».

Per altro noi siamo ben lungi dal potere fare per le curve dei valori ciò che il Keplero ha fatto per la curva descritta da Marte; anzi si potrebbe asserire forse che mai l'uomo potrà ciò compiere. È dunque necessario in qualche modo far si che più facile divenga il problema.

Osserviamo intanto che per quanto irregolare sia il diagramma che abbiamo segnato, i fatti reali lo sono anche più. Questi sono singole vendite, qualunque media noi facciamo è arbitraria, sostituisce un fenomeno ideale al reale. Ma è necessario battere questa via e potremmo essere ben lieti se ci riescisse di conoscere anche solo la legge delle variazioni di medie estesissime, trascurando ogni fatto particolare.

Ma non basta. Una legge generale del valore dovrebbe comprendere come casi particolari la legge del valore del grano come quella del valore del pane, delle paste dolci; la legge del valore del carbone, e quella del valore di quei pochi diamanti che per il straordinario pregio hanno fama nel mondo intero. È possibile trovare una tale legge? E se no, non giova dividere la materia in classi, ed esaminare ognuna paratamente?

Ciò è sempre stato fatto, e si fa, tanto dall'economia classica come dalla nuova scuola, ma alcune volte si dimentica, come interviene al Thornton, il quale muove alla teoria del valore molte obbiezioni, ed alcune di queste hanno solo motivo da ciò che egli fa proprie di vendite al minuto leggi che valgono solo per vendite all'ingrosso.

Ma oltre allo studio delle varie parti del fenomeno si sono cercate anche leggi generali. La tendenza della nuova scuola è manifestamente di spingersi più oltre della scuola classica in questa via. [409]

La nuova scuola considera un homo oeconomicus che sia perfetto edonista, e studia l'economia politica di quest'essere astratto ³⁾. Questo metodo è logicamente inreprensibile, purchè non si dimentichi mai che ogniqualvolta torneremo nel mondo reale dovremo fare vedere che in questo hanno valore le leggi che abbiamo trovato per gli uomini astratti considerali.'

★ La economia politica pura è in alcun modo simile alla meccanica razionale. Questa definisce l'ente astratto che chiama punto materiale, poi l'altro che ha nome sistema rigido, o corpo solido, e bastano quelle definizioni ad avvisarci che le conclusioni di quella scienza varranno pel fenomeno naturale solo in quanto sia in esso principale la qualità studiata dalla meccanica razionale. Man mano che vogliamo considerare altre proprietà dei corpi naturali siamo costretti di creare nuove astrazioni. Il corpo perfettamente elastico non ha esistenza più reale di quella del corpo perfettamente rigido. Vi sono corpi quasi isotropi in natura, non ve ne è di perfettamente isotropo.

Conviene dunque che guardiamo molto da vicino quali sono i postulati espliciti, ed impliciti, dei ragionamenti della nuova economia politica, per conoscere sin dove, e quando le sue leggi potranno avere valore nel mondo reale.

La teoria edonistica. Il Prof. Edgeworth ha saputo esporre nel modo più generalo, e col rigore matematico la nuova teoria, e qualunque modificazione vi arrechi il tempo sarà sempre degno di attento studio il libro intitolato Mathematical Psychics di quell'autore. [410]

Il Prof. Edgeworth ⁴⁾ dice schiettamente che considera l'uomo come una macchina pel piacere. Egli divide il calcolo del piacere in due. Il calcolo economico che investiga l'equilibrio di un sistema di forze edonistiche tendenti ciascuna a procacciare il massimo bene a ciascun individuo. Il calcolo utilitario (utilitarian calcutus) investiga l'equilibrio di un sistema in cui ciascuna forza e tutte tendono a procacciare la massima utilità per tutti.

Per tale modo non solo l'Economia Politica, ma anche la scienza della società umana, diventa un ramo del calcolo delle variazioni.

Questo concetto è mirabilmente semplico e grandioso ad un tempo. E ci pare pure che molta verità in sè racchiuda, ma per ciò appunto occorre procedere ben guardinghi per non trarre conclusioni, che ove fossero riconosciute contrarie all'esperienza, potrebbero travolgere e fare rigettare il bene e il male che vi può essere nelle nuove teorie.

Nulla diremo dei sentimenti altruisti in quanto sono opposti ai sentimenti egoisti, che suppone la teoria edonistica, non perchè l'argomento sia di poco peso, ma solo perchè ci pare quasi esaurito, dopo quanto su di esso fu detto dagli economisti e dai filosofi. Piuttosto vogliamo fare ora in generale due osservazioni sulle quali dovremo poi tornare spesso in casi particolari.

La prima è che sarebbe utile di spiegare meglio ciò che s'intende per piacere, cioè di considerare ciò che piace generalmente o in media, agli uomini delle nostro società.

Altrimenti si corre pericolo di incappare nel ragionamento in circolo. Se diciamo piacevole una cosa purchè solo piaccia ad un uomo qualsiasi; unicamente dalle azioni di quell'uomo potremo sapere ciò che a lui è piacevole o no; e non è lecito dopo di volere spiegare appunto quelle azioni col piacere che procurano all'uomo. [411]

La seconda è che non basta dare all'homo oeconomicus la qualità di perfetto edonista, ma che occorre anche decidere quali qualità di previdenza di ragionevolezza, ed altre sono a lui da concedersi. Queste qualità vedremo che gli vengono in un certo cotal grado implicitamente supposte. E ciò non ci pare bene; i postulati dovendo essere sempre dichiarati esplicitamente.

Utilità totale e grado finale di utilità. Consideriamo un individuo e due beni economici A e B, di cui esso possiede una certa quantità. Egli può godere direttamente A, oppure indirettamente trasformarlo in B. E analogamente per B. Il baratto è un modo di compiere quella trasformazione ma non è il solo.

Questo principio della trasformazione e dell'equivalenza dei beni informa il metodo geometrico col quale il Prof. Walras dimostra il teorema fondamentale del baratto ⁵⁾, ed è mirabile l'eleganza e la lucidità della sua esposizione.

Nella trasformazione di A in B. il numero di unità di A che occorre trasformare per avere un unità di B sarà detto il prezzo di B in A.

★ L'uso che noi qui facciamo di questa considerazione generale della trasfomazione non è molto utile per chi studia solo l'Economia Politica; ma chi ha anche studiato la termodinamica, o in genere la fìsica, ritrovasi ad usare una lingua già nota. La trasformazione dell' energia, l'equivalenza del calore col lavoro, ecc., sono analoghe alle trasformazioni economiche di cui il baratto è un caso.

L'utilità totale che ha un individuo dal possesso di A e di B è dal prof. Edgeworth figurata con una funzione delle quantità possedute.

Il Jevons, il Prof. Walras, il Prof. Marshall, ed altri invece di considerare l'utilità totale come una funzione qualsiasi delle quantità dei due beni posseduti, la considerano [412] come la somma di due funzioni, una della quantità di A, e l'altra della quantità di B.

Questa restrizione lascia per altro ancora molto generale l'espressione dell'utilità, la quale in quel modo può bastare per la maggior parte dei problemi economici, nulla vietando poi che per alcuni si abbandoni tale espressione.

Questa utilità totale ha esistenza reale? È presente alla coscienza dell'homo oeconomicus? Oppure è una semplice astrazione degli economisti? Di ciò tratteremo più innanzi, ora notiamo solo che gli economisti consentono che l'individuo considera piuttosto un'altra quantità da essi chiamata grado finale di utilità, o rareté (Walras) o marginal utility (dagli autori inglesi), la quale sarebbe propriamente l'utilità riferita all' unità di una quantità piccolissima di un bene aggiunto a quella già posseduta.

Supponiamo che i beni economici sieno indefinitamente divisibili. La considerazione della non divisibilità oltre un certo limite non presenta gravi difficoltà coi principii generali delle scienze e delle quantità.

Non sarà forse inutile di compendiare qui le notazioni adoperate dai valenti economisti che abbiamo rammentato, perchè il lettore possa più facilmente confrontare le nostre osservazioni coi testi di quegli autori.

Queste notazioni si riferiscono al caso in cui A si trasforma in B.

 

Utilità totale – Edgeworth	U = P = F (x, y)
Utilità totale – Walras

[413]

Si ponga mente che la x nella formula dell' Edgeworth è essen­zialmente negativa; e corrisponde alla –x dello Jevons.

Variazione infinitesima dell'Utilità totale

Il grado finale di utilità di una merce è la derivata parziale, rispetto a quella quantità di merce, dell'utilità totale.

L'utilità di una porzione infinitesima di merce dy, aggiunta a quella quantità y che già si possiede, è eguale al grado finale di utilità moltiplicato per dy. Naturalmente so scema la qualità di merce posseduta, dy è negativo.

L' utilità totale è la somma delle utilità di successive porzioni infinitesime di merce, ossia è l'integrale dell'utilità infinitesima.

Si suole prendere quest'integrale partendo da zero, ma ciò dà luogo a due inconvenienti.

1°. Quest'integrale può facilmente diventare infinito. Per esempio se

φ_1a(q)  =  a/q,

che è una forma che non si vede perchè si dovrebbe escludere a priori si ha

che per h = o diventa infinito.

2°. La considerazione degli elementi dell'integrale corrispondenti a una quantità zero di bene economico rende sempre più astratto l'integrale. [414]

Quanti uomini in un paese hanno coscienza delle sofferenze cagionate da una mancanza assoluta di nutrimento? Eppure quando l'integrale si prendo da zero si considera l'utilità che nasco dal rimuovere quelle sofferenze.

Crediamo quindi che sia meglio prendere quell' integrale partendo da una quantità positiva h, che si determinerà secondo i casi. E ciò non muta sostanzialmente le dimostrazioni degli autori che prendono quell'integrale partendo da zero.

Quando si considera l'utile nella trasformazione dei beni economici le variabili x e y non sono indipendenti, ma le condizioni colle quali si fanno la trasformazione stabiliscono tra di esse una relazione. Per esempio se si tratta di un baratto, come quello considerato da Jevons e da Walras, in cui ogni successiva porzione di bene barattato ha lo stesso prezzo si ha:

y/x = p

Il Marshall e l'Edgeworth hanno considerato il caso in cui le successivo porzioni dei beni barattati possono avere diversi prezzi. Allora x e y rimangono indipendenti sinquè non si sia fissato la legge che devono seguire quei successivi baratti.

Principio fondamentale del calcolo edonistico. Questo principio si può enunciare in due modi.

1°. Ogni uomo seguita la trasformazione dei beni economici in suo potere sinquè da essi ottenga la massima utilità totale.

2°. Ogni uomo seguita la trasformazione dei beni economici sinquè con questa operazione si può procurare un grado finale di utilità infinitesimo positivo.

Analiticamente questi due enunciati sono generalmente eguali, poiquè l'utilità totale è l'integrale del grado finale di utililà infinitesimo, e tanto vale dire che il primo è massimo, o che il secondo è zero. È vero che quest'ultima condizione contiene anche il caso del minimo, ma si esclude facilmente con considerazioni accessorie.

Ma se badiamo ai fatti concreti vi è questa differenza fra i due enunciati, che col primo si potrebbe supporre che un individuo ha coscienza dell'utilità totale di un bene economico. Questo ci pare accada molto di raro. Nessuno di [415] noi ha un chiaro concetto dell'utilità totale del mangiare, del bere, del vestire, dell'avere una casa ove ricovrarsi, ma solo ne intendiamo i vantaggi per piccole variazioni in più o in meno, cioè nella mente nostra cape solo il concetto del grado finale di utilità.

Anche analiticamente vi sono casi speciali nei quali non è indifferente ricorrere a l'uno piuttostochè all'altro enunciato.

Per gli aumenti positivi o negativi dx e dy delle merci possedute la variazione infinitissima dell' utilità sia

Q dx  +  R dy.

È sicuro che fino a quando non sarà zero gioverà, potendo, di seguitare le trasformazioni, in un senso se è positivo, nel senso opposto se è negativa. Questo è il secondo enunciato, che si vede quindi essere sempre vero.

Se Q e R sono le derivate parziali di una stessa funzione P, cioè se si può porre

∂P/∂x  =  Q  ,  ∂P/∂y  =  R

allora l'equazione per cui la variazione infinitesima dell' utilità è eguale a zero, è la condizione in virtù della quale P è un massimo (o un minimo) e il primo enunciato ha lo stesso valore del secondo.

Ma può darsi benissimo il caso che P e Q non sieno le derivate parziali di una stessa funzione, e allora non esiste la funzione per la quale avrebbe valore il primo enunciato.

Concludiamo quindi che il secondo enunciato è da preferirsi sia rispetto ai fatti concreti come ai ragionameti analitici.

★ Il lettore che ha in pratica la meccanica razionale si è già accorto della perfetta corrispondenza tra queste formole e quelle della meccanica.

★ Se Q è la forza che agisce su un punto materiale secondo l'asse delle x, P quella che agisce secondo l'asse delle y, e se ∂x e ∂y sono i movimenti che può prendere il punto compatibilmente coi legami, l'equazione di Lagrangia

(1)     Q δx  +  R δy  =  0,

per l'equilibrio del punto è identica a quella che otteniamo eguagliando a zero la variazione infinitesima dell'utilità. [416]

* Si sa che se Q e R sono le derivate parziali di una stessa funzione P, questa nei caso dell'equilibrio stabile è un massimo, e nel caso dell'equilibrio instabile e un minimo.

――――――――

1) Logica, lib. VI, cap. VII. 

2) Mill, loc. cit, lib. VI. cap. VIII. 

3) I principii di Economia pura del Prof. Pantaleoni (Firenze 1889) sono assai notevoli per la lucidità colla quale espongono queste teorie. La lettura di quel libro ci ha suggerito molte fra le considerazioni che esponiamo in quest'articolo, e ci hanno fatto chiare assai idee che la lettura di altri scritti ci avevano lasciate oscure. E dobbiamo pure ringraziare quel nostro amico per molti suggerimenti che assai ci giovarono nel comporre questo scritto. 

4) Mathematical Psychics – London, C. Kegan Paul et C.°, 1881 pag. 15. 

5) Walras, De l'échange de plusieurs marchandises entre elles – Mémoires de la Societé des Ingénieurs civils. Paris, janvier, 1891. 

6) La forma a + x, y è solo notata per stare in armonia colle altre notazioni. Propriamente lo Edgeworth loc. cit. p. 34 dice che «La x figura il sacrifizio oggettivamente misurato che può essere lavoro manuale eseguito, o merce, o capitale risparmiato per un certo tempo, e la y figura l'oggettivo compenso dell'individuo che si considera». 

7) Per chi non avesse molto in pratica i simboli matematici sarà forse bene ricordaro che ∂P/∂x è la derivata parziale di P, presa supponendo y costante. E si indicherà con dP il differenziale totale di P quando le variabili indipendenti x e y variano. Al solito dP/dx sarà la derivata di P in cui y è considerata funzione di x. Analoghe notazioni valgono per y.