Tractatus Logico-Philosophicus

4

Der Gedanke ist der sinnvolle Satz.

4.001

Die Gesamtheit der Sätze ist die Sprache.

4.002

Der Mensch besitzt die Fähigkeit Sprachen zu bauen, womit sich jeder Sinn ausdrücken lässt, ohne eine Ahnung davon zu haben, wie und was jedes Wort bedeutet. – Wie man auch spricht, ohne zu wissen, wie die einzelnen Laute hervorgebracht werden. Die Umgangssprache ist ein Teil des menschlichen Organismus und nicht weniger kompliziert als dieser. Es ist menschenunmöglich, die Sprachlogik aus ihr unmittelbar zu entnehmen. Die Sprache verkleidet den Gedanken. Und zwar so, dass man nach der äusseren Form des Kleides, nicht auf die Form des bekleideten Gedankens schliessen kann; weil die äussere Form des Kleides nach ganz anderen Zwecken gebildet ist, als danach, die Form des Körpers erkennen zu lassen. Die stillschweigenden Abmachungen zum Verständnis der Umgangssprache sind enorm kompliziert.

4.003

Die meisten Sätze und Fragen, welche über philosophische Dinge geschrieben worden sind, sind nicht falsch, sondern unsinnig. Wir können daher Fragen dieser Art überhaupt nicht beantworten, sondern nur ihre Unsinnigkeit feststellen. Die meisten Fragen und Sätze der Philosophen beruhen darauf, dass wir unsere Sprachlogik nicht verstehen. (Sie sind von der Art der Frage, ob das Gute mehr oder weniger identisch sei als das Schöne.) Und es ist nicht verwunderlich, dass die tiefsten Probleme eigentlich keine Probleme sind.

4.0031

Alle Philosophie ist „Sprachkritik“. (Allerdings nicht im Sinne Mauthners.) Russell's Verdienst ist es, gezeigt zu haben, dass die scheinbare logische Form des Satzes nicht seine wirkliche sein muss.

4.031

Man sagte einmal, dass Gott alles schaffen könne, nur nichts, was den logischen Gesetzen zuwider wäre. – Wir könnten nämlich von einer „unlogischen“ Welt nicht sagen, wie sie aussähe.

4.01

Der Satz ist ein Bild der Wirklichkeit. Der Satz ist ein Modell der Wirklichkeit, so wie wir sie uns denken.

4.011

Auf den ersten Blick scheint der Satz – wie er etwa auf dem Papier gedruckt steht – kein Bild der Wirklichkeit zu sein, von der er handelt. Aber auch die Notenschrift scheint auf den ersten Blick kein Bild der Musik zu sein, und unsere Lautzeichen- (Buchstaben-)Schrift kein Bild unserer Lautsprache. Und doch erweisen sich diese Zeichensprachen auch im gewöhnlichen Sinne als Bilder dessen, was sie darstellen.

4.012

Offenbar ist, dass wir einen Satz von der Form „aRb“ als Bild empfinden. Hier ist das Zeichen offenbar ein Gleichnis des Bezeichneten.

4.013

Und wenn wir in das Wesentliche dieser Bildhaftigkeit eindringen, so sehen wir, dass dieselbe durch scheinbare Unregelmässigkeiten (wie die Verwendung der ♯ und ♭ in der Notenschrift) nicht gestört wird. Denn auch diese Unregelmässigkeiten bilden das ab, was sie ausdrücken sollen; nur auf eine andere Art und Weise.

4.014

Die Grammophonplatte, der musikalische Gedanke, die Notenschrift, die Schallwellen, stehen alle in jener abbildenden internen Beziehung zu einander, die zwischen Sprache und Welt besteht. Ihnen allen ist der logische Bau gemeinsam. (Wie im Märchen die zwei Jünglinge, ihre zwei Pferde und ihre Lilien. Sie sind alle in gewissem Sinne Eins.)

4.0141

Dass es eine allgemeine Regel gibt, durch die der Musiker aus der Partitur die Symphonie entnehmen kann, durch welche man aus der Linie auf der Grammophonplatte die Symphonie und nach der ersten Regel wieder die Partitur ableiten kann, darin besteht eben die innere Ähnlichkeit dieser scheinbar so ganz verschiedenen Gebilde. Und jene Regel ist das Gesetz der Projektion, welches die Symphonie in die Notensprache projiziert. Sie ist die Regel der Übersetzung der Notensprache in die Sprache der Grammophonplatte.

4.015

Die Möglichkeit aller Gleichnisse, der ganzen Bildhaftigkeit unserer Ausdrucksweise, ruht in der Logik der Abbildung.

4.016

Um das Wesen des Satzes zu verstehen, denken wir an die Hieroglyphenschrift, welche die Tatsachen die sie beschreibt abbildet. Und aus ihr wurde die Buchstabenschrift, ohne das Wesentliche der Abbildung zu verlieren.

4.02

Dies sehen wir daraus, dass wir den Sinn des Satzzeichens verstehen, ohne dass er uns erklärt wurde.

4.021

Der Satz ist ein Bild der Wirklichkeit: Denn ich kenne die von ihm dargestellte Sachlage, wenn ich den Satz verstehe. Und den Satz verstehe ich, ohne dass mir sein Sinn erklärt wurde.

4.022

Der Satz zeigt seinen Sinn. Der Satz zeigt, wie es sich verhält, wenn er wahr ist. Und er sagt, dass es sich so verhält.

4.023

Die Wirklichkeit muss durch den Satz auf ja oder nein fixiert sein. Dazu muss sie durch ihn vollständig beschrieben werden. Der Satz ist die Beschreibung eines Sachverhaltes. Wie die Beschreibung einen Gegenstand nach seinen externen Eigenschaften, so beschreibt der Satz die Wirklichkeit nach ihren internen Eigenschaften. Der Satz konstruiert eine Welt mit Hilfe eines logischen Gerüstes und darum kann man am Satz auch sehen, wie sich alles Logische verhält, wenn er wahr ist. Man kann aus einem falschen Satz Schlüsse ziehen.

4.024

Einen Satz verstehen, heisst, wissen was der Fall ist, wenn er wahr ist. (Man kann ihn also verstehen, ohne zu wissen, ob er wahr ist.) Man versteht ihn, wenn man seine Bestandteile versteht.

4.025

Die Übersetzung einer Sprache in eine andere geht nicht so vor sich, dass man jeden Satz, der einen in einen Satz der anderen übersetzt, sondern nur die Satzbestandteile werden übersetzt. (Und das Wörterbuch übersetzt nicht nur Substantiva, sondern auch Zeit-, Eigenschafts- und Bindewörter etc.; und es behandelt sie alle gleich.)

4.026

Die Bedeutungen der einfachen Zeichen (der Wörter) müssen uns erklärt werden, dass wir sie verstehen. Mit den Sätzen aber verständigen wir uns.

4.027

Es liegt im Wesen des Satzes, dass er uns einen neuen Sinn mitteilen kann.

4.03

Ein Satz muss mit alten Ausdrücken einen neuen Sinn mitteilen. Der Satz teilt uns eine Sachlage mit, also muss er wesentlich mit der Sachlage zusammenhängen. Und der Zusammenhang ist eben, dass er ihr logisches Bild ist. Der Satz sagt nur insoweit etwas aus, als er ein Bild ist.

4.031

Im Satz wird gleichsam eine Sachlage probeweise zusammengestellt. Man kann geradezu sagen: statt, dieser Satz hat diesen und diesen Sinn; dieser Satz stellt diese und diese Sachlage dar.

4.0311

Ein Name steht für ein Ding, ein anderer für ein anderes Ding und untereinander sind sie verbunden, so stellt das Ganze – wie ein lebendes Bild – den Sachverhalt vor.

4.0312

Die Möglichkeit des Satzes beruht auf dem Prinzip der Vertretung von Gegenständen durch Zeichen. Mein Grundgedanke ist, dass die „logischen Konstanten“ nicht vertreten. Dass sich die Logik der Tatsachen nicht vertreten lässt.

4.032

Nur insoweit ist der Satz ein Bild einer Sachlage, als er logisch gegliedert ist. (Auch der Satz „ambulo“ ist zusammengesetzt, denn sein Stamm ergibt mit einer anderen Endung und seine Endung mit einem anderen Stamm, einen anderen Sinn.)

4.04

Am Satz muss gerade soviel zu unterscheiden sein, als an der Sachlage die er darstellt. Die beiden müssen die gleiche logische (mathematische) Mannigfaltigkeit besitzen. (Vergleiche Hertz's Mechanik, über Dynamische Modelle.)

4.041

Diese mathematische Mannigfaltigkeit kann man natürlich nicht selbst wieder abbilden. Aus ihr kann man beim Abbilden nicht heraus.

4.0411

Wollten wir z. B. das, was wir durch „(x)fx“ ausdrücken, durch Vorsetzen eines Indexes vor „fx“ ausdrücken – etwa so: „Alg. fx“, es würde nicht genügen – wir wüssten nicht, was verallgemeinert wurde. Wollten wir es durch einen Index „a“ anzeigen – etwa so: „f (x_a)“ – es würde auch nicht genügen – wir wüssten nicht den Bereich der Allgemeinheitsbezeichnung. Wollten wir es durch Einführung einer Marke in die Argumentstellen versuchen – etwa so: „(A, A) . F (A, A)“ – es würde nicht genügen – wir könnten die Identität der Variablen nicht feststellen, u. s. w. Alle diese Bezeichnungsweisen genügen nicht, weil sie nicht die notwendige mathematische Mannigfaltigkeit haben.

4.0412

Aus demselben Grunde genügt die idealistische Erklärung des Sehens der räumlichen Beziehungen durch die „Raumbrille“ nicht, weil sie nicht die Mannigfaltigkeit dieser Beziehungen erklären kann.

4.05

Die Wirklichkeit wird mit dem Satz verglichen.

4.06

Nur dadurch kann der Satz wahr oder falsch sein, indem er ein Bild der Wirklichkeit ist.

4.061

Beachtet man nicht, dass der Satz einen von den Tatsachen unabhängigen Sinn hat, so kann man leicht glauben, dass wahr und falsch gleichberechtigte Beziehungen von Zeichen und Bezeichnetem sind. Man könnte dann z. B. sagen, dass „p“ auf die wahre Art bezeichnet, was „?p“ auf die falsche Art, etc.

4.062

Kann man sich nicht mit falschen Sätzen, wie bisher mit wahren, verständigen? Solange man nur weiss, dass sie falsch gemeint sind. Nein! Denn, wahr ist ein Satz, wenn es sich so verhält, wie wir es durch ihn sagen; und wenn wir mit „p“ ∼p meinen, und es sich so verhält wie wir es meinen, so ist „p“ in der neuen Auffassung wahr und nicht falsch.

4.0621

Dass aber die Zeichen „p“ und „∼p“ das gleiche sagen können, ist wichtig. Denn es zeigt, dass dem Zeichen „∼“ in der Wirklichkeit nichts entspricht. Dass in einem Satz die Verneinung vorkommt, ist noch kein Merkmal seines Sinnes (∼∼p = p). Die Sätze „p“ und „∼p“ haben entgegengesetzten Sinn, aber es entspricht ihnen eine und dieselbe Wirklichkeit.

4.063

Ein Bild zur Erklärung des Wahrheitsbegriffes: Schwarzer Fleck auf weissem Papier; die Form des Fleckes kann man beschreiben, indem man für jeden Punkt der Fläche angibt, ob er weiss oder schwarz ist. Der Tatsache, dass ein Punkt schwarz ist, entspricht eine positive – der, dass ein Punkt weiss (nicht schwarz) ist, eine negative Tatsache. Bezeichne ich einen Punkt der Fläche (einen Frege'schen Wahrheitswert), so entspricht dies der Annahme, die zur Beurteilung aufgestellt wird, etc. etc. Um aber sagen zu können, ein Punkt sei schwarz oder weiss, muss ich vorerst wissen, wann man einen Punkt schwarz und wann man ihn weiss nennt; um sagen zu können: „p“ ist wahr (oder falsch), muss ich bestimmt haben, unter welchen Umständen ich „p“ wahr nenne, und damit bestimme ich den Sinn des Satzes. Der Punkt an dem das Gleichnis hinkt ist nun der: Wir können auf einen Punkt des Papiers zeigen, auch ohne zu wissen, was weiss und schwarz ist; einem Satz ohne Sinn aber entspricht gar nichts, denn er bezeichnet kein Ding (Wahrheitswert) dessen Eigenschaften etwa „falsch“ oder „wahr“ hiessen; das Verbum eines Satzes ist nicht „ist wahr“ oder „ist falsch“ – wie Frege glaubte –, sondern das, was „wahr ist“ muss das Verbum schon enthalten.

4.064

Jeder Satz muss schon einen Sinn haben; die Bejahung kann ihn ihm nicht geben, denn sie bejaht ja gerade den Sinn. Und dasselbe gilt von der Verneinung, etc.

4.0641

Man könnte sagen: Die Verneinung bezieht sich schon auf den logischen Ort, den der verneinte Satz bestimmt. Der verneinende Satz bestimmt einen anderen logischen Ort als der verneinte. Der verneinende Satz bestimmt einen logischen Ort mit Hilfe des logischen Ortes des verneinten Satzes, indem er jenen als ausserhalb diesem liegend beschreibt. Dass man den verneinten Satz wieder verneinen kann, zeigt schon, dass das, was verneint wird, schon ein Satz und nicht erst die Vorbereitung zu einem Satze ist.

4.1

Der Satz stellt das Bestehen und Nichtbestehen der Sachverhalte dar.

4.11

Die Gesamtheit der wahren Sätze ist die gesamte Naturwissenschaft (oder die Gesamtheit der Naturwissenschaften).

4.111

Die Philosophie ist keine der Naturwissenschaften. (Das Wort „Philosophie“ muss etwas bedeuten, was über oder unter, aber nicht neben den Naturwissenschaften steht.)

4.112

Der Zweck der Philosophie ist die logische Klärung der Gedanken. Die Philosophie ist keine Lehre, sondern eine Tätigkeit. Ein philosophisches Werk besteht wesentlich aus Erläuterungen. Das Resultat der Philosophie sind nicht „philosophische Sätze“, sondern das Klarwerden von Sätzen. Die Philosophie soll die Gedanken, die sonst, gleichsam, trübe und verschwommen sind, klar machen und scharf abgrenzen.

4.1121

Die Psychologie ist der Philosophie nicht verwandter als irgend eine andere Naturwissenschaft. Erkenntnistheorie ist die Philosophie der Psychologie. Entspricht nicht mein Studium der Zeichensprache dem Studium der Denkprozesse, welches die Philosophen für die Philosophie der Logik für so wesentlich hielten? Nur verwickelten sie sich meistens in unwesentliche psychologische Untersuchungen und eine analoge Gefahr gibt es auch bei meiner Methode.

4.1122

Die Darwinsche Theorie hat mit der Philosophie nicht mehr zu schaffen, als irgend eine andere Hypothese der Naturwissenschaft.

4.113

Die Philosophie begrenzt das bestreitbare Gebiet der Naturwissenschaft.

4.114

Sie soll das Denkbare abgrenzen und damit das Undenkbare. Sie soll das Undenkbare von innen durch das Denkbare begrenzen.

4.115

Sie wird das Unsagbare bedeuten, indem sie das Sagbare klar darstellt.

4.116

Alles, was überhaupt gedacht werden kann, kann klar gedacht werden. Alles was sich aussprechen lässt, lässt sich klar aussprechen.

4.12

Der Satz kann die gesamte Wirklichkeit darstellen, aber er kann nicht das darstellen, was er mit der Wirklichkeit gemein haben muss, um sie darstellen zu können – die logische Form. Um die logische Form darstellen zu können, müssten wir uns mit dem Satze ausserhalb der Logik aufstellen können, das heisst ausserhalb der Welt.

4.121

Der Satz kann die logische Form nicht darstellen, sie spiegelt sich in ihm. Was sich in der Sprache spiegelt, kann sie nicht darstellen. Was sich in der Sprache ausdrückt, können wir nicht durch sie ausdrücken. Der Satz zeigt die logische Form der Wirklichkeit. Er weist sie auf.

4.1211

So zeigt ein Satz „fa“, dass in seinem Sinn der Gegenstand a vorkommt, zwei Sätze „fa“ und „ga“, dass in ihnen beiden von demselben Gegenstand die Rede ist. Wenn zwei Sätze einander widersprechen, so zeigt dies ihre Struktur; ebenso, wenn einer aus dem anderen folgt, u. s. w.

4.1212

Was gezeigt werden kann, kann nicht gesagt werden.

4.1213

Jetzt verstehen wir auch unser Gefühl: dass wir im Besitze einer richtigen logischen Auffassung seien, wenn nur einmal alles in unserer Zeichensprache stimmt.

4.122

Wir können in gewissem Sinne von formalen Eigenschaften der Gegenstände und Sachverhalte bezw. von Eigenschaften der Struktur der Tatsachen reden und in demselben Sinne von formalen Relationen und Relationen von Strukturen. (Statt Eigenschaft der Struktur sage ich auch „interne Eigenschaft“; statt Relation der Strukturen „interne Relation“. Ich führe diese Ausdrücke ein, um den Grund der, bei den Philosophen sehr verbreiteten Verwechslung zwischen den internen Relationen und den eigentlichen (externen) Relationen zu zeigen.) Das Bestehen solcher interner Eigenschaften und Relationen kann aber nicht durch Sätze behauptet werden, sondern es zeigt sich in den Sätzen, welche jene Sachverhalte darstellen und von jenen Gegenständen handeln.

4.1221

Eine interne Eigenschaft einer Tatsache können wir auch einen Zug dieser Tatsache nennen. (In dem Sinn, in welchem wir etwa von Gesichtszügen sprechen.)

4.123

Eine Eigenschaft ist intern, wenn es undenkbar ist, dass ihr Gegenstand sie nicht besitzt. (Diese blaue Farbe und jene stehen in der internen Relation von heller und dunkler eo ipso. Es ist undenkbar, dass diese beiden Gegenstände nicht in dieser Relation stünden.) (Hier entspricht dem schwankenden Gebrauch der Worte „Eigenschaft“ und „Relation“ der schwankende Gebrauch des Wortes „Gegenstand“.)

4.124

Das Bestehen einer internen Eigenschaft einer möglichen Sachlage wird nicht durch einen Satz ausgedrückt, sondern es drückt sich in dem sie darstellenden Satz, durch eine interne Eigenschaft dieses Satzes aus. Es wäre ebenso unsinnig, dem Satze eine formale Eigenschaft zuzusprechen, als sie ihm abzusprechen.

4.1241

Formen kann man nicht dadurch von einander unterscheiden, dass man sagt, die eine habe diese, die andere aber jene Eigenschaft; denn dies setzt voraus, dass es einen Sinn habe, beide Eigenschaften von beiden Formen auszusagen.

4.125

Das Bestehen einer internen Relation zwischen möglichen Sachlagen drückt sich sprachlich durch eine interne Relation zwischen den sie darstellenden Sätzen aus.

4.1251

Hier erledigt sich nun die Streitfrage „ob alle Relationen intern oder extern“ seien.

4.1252

Reihen, welche durch interne Relationen geordnet sind, nenne ich Formenreihen. Die Zahlenreihe ist nicht nach einer externen, sondern nach einer internen Relation geordnet. Ebenso die Reihe der Sätze „aRb“, „(∃x) : aRx . xRb“,„(∃x, y) : aRx . xRy . yRb“, u. s. f. (Steht b in einer dieser Beziehungen zu a, so nenne ich b einen Nachfolger von a.)

4.126

In dem Sinne, in welchem wir von formalen Eigenschaften sprechen, können wir nun auch von formalen Begriffen reden. (Ich führe diesen Ausdruck ein, um den Grund der Verwechslung der formalen Begriffe mit den eigentlichen Begriffen, welche die ganze alte Logik durchzieht, klar zu machen.) Dass etwas unter einen formalen Begriff als dessen Gegenstand fällt, kann nicht durch einen Satz ausgedrückt werden. Sondern es zeigt sich an dem Zeichen dieses Gegenstandes selbst. (Der Name zeigt, dass er einen Gegenstand bezeichnet, das Zahlenzeichen, dass es eine Zahl bezeichnet etc.) Die formalen Begriffe können ja nicht, wie die eigentlichen Begriffe, durch eine Funktion dargestellt werden. Denn ihre Merkmale, die formalen Eigenschaften, werden nicht durch Funktionen ausgedrückt. Der Ausdruck der formalen Eigenschaft ist ein Zug gewisser Symbole. Das Zeichen der Merkmale eines formalen Begriffes ist also ein charakteristischer Zug aller Symbole, deren Bedeutungen unter den Begriff fallen. Der Ausdruck des formalen Begriffes also, eine Satzvariable, in welcher nur dieser charakteristische Zug konstant ist.

4.127

Die Satzvariable bezeichnet den formalen Begriff und ihre Werte die Gegenstände, welche unter diesen Begriff fallen.

4.1271

Jede Variable ist das Zeichen eines formalen Begriffes. Denn jede Variable stellt eine konstante Form dar, welche alle ihre Werte besitzen, und die als formale Eigenschaft dieser Werte aufgefasst werden kann.

4.1272

So ist der variable Name „x“ das eigentliche Zeichen des Scheinbegriffes Gegenstand. Wo immer das Wort „Gegenstand“ („Ding“, „Sache“, etc.) richtig gebraucht wird, wird es in der Begriffsschrift durch den variablen Namen ausgedrückt. Zum Beispiel in dem Satz „es gibt 2 Gegenstände, welche . . . “ durch „(∃x, y) . . .“. Wo immer es anders, also als eigentliches Begriffswort gebraucht wird, entstehen unsinnige Scheinsätze. So kann man z. B. nicht sagen „Es gibt Gegenstände“, wie man etwa sagt „Es gibt Bücher“. Und ebenso wenig „Es gibt 100 Gegenstände“, oder „Es gibt ℵ0 Gegenstände“. Und es ist unsinnig, von der Anzahl aller Gegenstände zu sprechen. Dasselbe gilt von den Worten „Komplex“, „Tatsache“, „Funktion“, „Zahl“, etc. Sie alle bezeichnen formale Begriffe und werden in der Begriffsschrift durch Variable, nicht durch Funktionen oder Klassen dargestellt. (Wie Frege und Russell glaubten.) Ausdrücke wie „1 ist eine Zahl“, „es gibt nur Eine Null“ und alle ähnlichen sind unsinnig. (Es ist ebenso unsinnig zu sagen „es gibt nur eine 1“, als es unsinnig wäre, zu sagen: 2 + 2 ist um 3 Uhr gleich 4.)

4.12721

Der formale Begriff ist mit einem Gegenstand, der unter ihn fällt, bereits gegeben. Man kann also nicht Gegenstände eines formalen Begriffes und den formalen Begriff selbst als Grundbegriffe einführen. Man kann also z. B. nicht den Begriff der Funktion, und auch spezielle Funktionen (wie Russell) als Grundbegriffe einführen; oder den Begriff der Zahl und bestimmte Zahlen.

4.1273

Wollen wir den allgemeinen Satz: „b ist ein Nachfolger von a“ in der Begriffsschrift ausdrücken, so brauchen wir hierzu einen Ausdruck für das allgemeine Glied der Formenreihe: aRb, (∃x) : aRx.xRb, (∃x, y) : aRx.xRy.yRb, . . . Das allgemeine Glied einer Formenreihe kann man nur durch eine Variable ausdrücken, denn der Begriff: Glied dieser Formenreihe, ist ein formaler Begriff. (Dies haben Frege und Russell übersehen; die Art und Weise wie sie allgemeine Sätze, wie den obigen ausdrücken wollen ist daher falsch; sie enthält einen circulus vitiosus.) Wir können das allgemeine Glied der Formenreihe bestimmen, indem wir ihr erstes Glied angeben und die allgemeine Form der Operation, welche das folgende Glied aus dem vorhergehenden Satz erzeugt.

4.128

Die logischen Formen sind zahllos. Darum gibt es in der Logik keine ausgezeichneten Zahlen und darum gibt es keinen philosophischen Monismus oder Dualismus, etc.

4.2

Der Sinn des Satzes ist seine Übereinstimmung, und Nichtübereinstimmung mit den Möglichkeiten des Bestehens und Nichtbestehens der Sachverhalte.

4.21

Der einfachste Satz, der Elementarsatz, behauptet das Bestehen eines Sachverhaltes.

4.211

Ein Zeichen des Elementarsatzes ist es, dass kein Elementarsatz mit ihm in Widerspruch stehen kann.

4.22

Der Elementarsatz besteht aus Namen. Er ist ein Zusammenhang, eine Verkettung, von Namen.

4.221

Es ist offenbar, dass wir bei der Analyse der Sätze auf Elementarsätze kommen müssen, die aus Namen in unmittelbarer Verbindung bestehen. Es frägt sich hier, wie kommt der Satzverband zustande.

4.2211

Auch wenn die Welt unendlich komplex ist, so dass jede Tatsache aus unendlich vielen Sachverhalten besteht und jeder Sachverhalt aus unendlich vielen Gegenständen zusammengesetzt ist, auch dann müsste es Gegenstände und Sachverhalte geben.

4.23

Der Name kommt im Satz nur im Zusammenhange des Elementarsatzes vor.

4.24

Die Namen sind die einfachen Symbole, ich deute sie durch einzelne Buchstaben („x“, „y“, „z“) an.Den Elementarsatz schreibe ich als Funktion der Namen in der Form: „fx“, „φ(x, y)“, etc. Oder ich deute ihn durch die Buchstaben p, q, r an.

4.241

Gebrauche ich zwei Zeichen in ein und derselben Bedeutung, so drücke ich dies aus, indem ich zwischen beide das Zeichen „=“ setze. „a = b“ heisst also: das Zeichen „a“ ist durch das Zeichen „b“ ersetzbar. (Führe ich durch eine Gleichung ein neues Zeichen „b“ ein, indem ich bestimme, es solle ein bereits bekanntes Zeichen „a“ ersetzen, so schreibe ich die Gleichung – Definition – (wie Russell) in der Form „a = b Def.“. Die Definition ist eine Zeichenregel.)

4.242

Ausdrücke von der Form „a = b“ sind also nur Behelfe der Darstellung; sie sagen nichts über die Bedeutung der Zeichen „a“, „b“ aus.

4.243

Können wir zwei Namen verstehen, ohne zu wissen, ob sie dasselbe Ding oder zwei verschiedene Dinge bezeichnen? – Können wir einen Satz, worin zwei Namen vorkommen, verstehen, ohne zu wissen, ob sie Dasselbe oder Verschiedenes bedeuten? Kenne ich etwa die Bedeutung eines englischen und eines gleichbedeutenden deutschen Wortes, so ist es unmöglich, dass ich nicht weiss, dass die beiden gleichbedeutend sind; es ist unmöglich, dass ich sie nicht ineinander übersetzen kann. Ausdrücke wie „a = a“, oder von diesen abgeleitete, sind weder Elementarsätze, noch sonst sinnvolle Zeichen. (Dies wird sich später zeigen.)

4.25

Ist der Elementarsatz wahr, so besteht der Sachverhalt; ist der Elementarsatz falsch, so besteht der Sachverhalt nicht.

4.26

Die Angabe aller wahren Elementarsätze beschreibt die Welt vollständig. Die Welt ist vollständig beschrieben durch die Angaben aller Elementarsätze plus der Angabe, welche von ihnen wahr und welche falsch sind.

4.27

Bezüglich des Bestehens und Nichtbestehens von n Sachverhalten gibt es Möglichkeiten. Es können alle Kombinationen der Sachverhalte bestehen, die andern nicht bestehen.

4.28

Diesen Kombinationen entsprechen ebenso viele Möglichkeiten der Wahrheit – und Falschheit – von n Elementarsätzen.

4.3

Die Wahrheitsmöglichkeiten der Elementarsätze bedeuten die Möglichkeiten des Bestehens und Nichtbestehens der Sachverhalte.

4.31

Die Wahrheitsmöglichkeiten können wir durch Schemata folgender Art darstellen („W“ bedeutet „wahr“, „F“, „falsch“. Die Reihen der „W“ und „F“ unter der Reihe der Elementarsätze bedeuten in leichtverständlicher Symbolik deren Wahrheitsmöglichkeiten):

4.4

Der Satz ist der Ausdruck der Übereinstimmung und Nichtübereinstimmung mit den Wahrheitsmöglichkeiten der Elementarsätze.

4.41

Die Wahrheitsmöglichkeiten der Elementarsätze sind die Bedingungen der Wahrheit und Falschheit der Sätze.

4.411

Es ist von vornherein wahrscheinlich, dass die Einführung der Elementarsätze für das Verständnis aller anderen Satzarten grundlegend ist. Ja, das Verständnis der allgemeinen Sätze hängt fühlbar von dem der Elementar­sätze ab.

4.42

Bezüglich der Übereinstimmung und Nichtübereinstim­mung eines Satzes mit den Wahrheitsmöglichkeiten von n Elementarsätzen gibt es

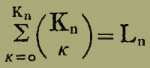
Möglichkeiten.

4.43

Die Übereinstimmung mit den Wahrheitsmöglichkeiten können wir dadurch ausdrücken, indem wir ihnen im Schema etwa das Abzeichen „W“ (wahr) zuordnen. Das Fehlen dieses Abzeichens bedeutet die Nichtübereinstimmung.

4.431

Der Ausdruck der Übereinstimmung und Nichtübereinstimmung mit den Wahrheitsmöglichkeiten der Elementarsätze drückt die Wahrheitsbedingungen des Satzes aus. Der Satz ist der Ausdruck seiner Wahrheitsbedingungen. (Frege hat sie daher ganz richtig als Erklärung der Zeichen seiner Begriffsschrift vorausgeschickt. Nur ist die Erklärung des Wahrheitsbegriffes bei Frege falsch: Wären „das Wahre“ und „das Falsche“ wirklich Gegenstände und die Argumente in ~p etc. dann wäre nach Frege's Bestimmung der Sinn von „~p“ keineswegs bestimmt.)

4.44

Das Zeichen, welches durch die Zuordnung jener Abzeichen „W“ und der Wahrheitsmöglichkeiten entsteht, ist ein Satzzeichen.

4.441

Es ist klar, dass dem Komplex der Zeichen „F“ und „W“ kein Gegenstand (oder Komplex von Gegenständen) entspricht; so wenig, wie den horizontalen und vertikalen Strichen oder den Klammern. – „Logische Gegenstände“ gibt es nicht. Analoges gilt natürlich für alle Zeichen, die dasselbe ausdrücken wie die Schemata der „W“ und „F“.

4.442

Es ist z. B.:

ein Satzzeichen. (Frege's „Urteilsstrich“ „⊦“ ist logisch ganz bedeutungslos; er zeigt bei Frege (und Russell) nur an, dass diese Autoren die so bezeichneten Sätze für wahr halten. „⊦“ gehört daher ebenso wenig zum Satzgefüge, wie etwa die Nummer des Satzes. Ein Satz kann unmöglich von sich selbst aussagen, dass er wahr ist.) Ist die Reihenfolge der Wahrheitsmöglichkeiten im Schema durch eine Kombinationsregel ein für allemal festgesetzt, dann ist die letzte Kolonne allein schon ein Ausdruck der Wahrheitsbedingungen. Schreiben wir diese Kolonne als Reihe hin, so wird das Satzzeichen zu: „(WW–W)(p, q)“ oder deutlicher „(WWFW)(p, q)“. (Die Anzahl der Stellen in der linken Klammer ist durch die Anzahl der Glieder in der rechten bestimmt.)

4.45

Für n Elementarsätze gibt es Ln mögliche Gruppen von Wahrheitsbedingungen. Die Gruppen von Wahrheits­bedingungen, welche zu den Wahrheitsmöglichkeiten einer Anzahl von Elementarsätzen gehören, lassen sich in eine Reihe ordnen.

4.46

Unter den möglichen Gruppen von Wahrheitsbedin­gungen gibt es zwei extreme Fälle. In dem einen Fall ist der Satz für sämtliche Wahrheitsmöglichkeiten der Elemen­tarsätze wahr. Wir sagen, die Wahrheitsbedingungen sind tautologisch. Im zweiten Fall ist der Satz für sämtliche Wahrheitsmöglichkeiten falsch: Die Wahrheitsbedin­gungen sind kontradiktorisch. Im ersten Fall nennen wir den Satz eine Tautologie, im zweiten Fall eine Kontradiktion.

4.461

Der Satz zeigt was er sagt, die Tautologie und die Kontradiktion, dass sie nichts sagen. Die Tautologie hat keine Wahrheitsbedingungen, denn sie ist bedingungslos wahr; und die Kontradiktion ist unter keiner Bedingung wahr. Tautologie und Kontradiktion sind sinnlos. (Wie der Punkt von dem zwei Pfeile in entgegengesetzter Richtung auseinandergehen.) (Ich weiss z. B. nichts über das Wetter, wenn ich weiss, dass es regnet oder nicht regnet.)

4.4611

Tautologie und Kontradiktion sind aber nicht unsinnig; sie gehören zum Symbolismus, und zwar ähnlich wie die „0“ zum Symbolismus der Arithmetik.

4.462

Tautologie und Kontradiktion sind nicht Bilder der Wirklichkeit. Sie stellen keine mögliche Sachlage dar. Denn jene lässt jede mögliche Sachlage zu, diese keine. In der Tautologie heben die Bedingungen der Übereinstimmung mit der Welt – die darstellenden Beziehungen – einander auf, so dass sie in keiner darstellenden Beziehung zur Wirklichkeit steht.

4.463

Die Wahrheitsbedingungen bestimmen den Spielraum, der den Tatsachen durch den Satz gelassen wird. (Der Satz, das Bild, das Modell, sind im negativen Sinne wie ein fester Körper, der die Bewegungsfreiheit der anderen beschränkt; im positiven Sinne, wie der von fester Substanz begrenzte Raum, worin ein Körper Platz hat.) Die Tautologie lässt der Wirklichkeit den ganzen – unendlichen – logischen Raum; die Kontradiktion erfüllt den ganzen logischen Raum und lässt der Wirklichkeit keinen Punkt. Keine von beiden kann daher die Wirklichkeit irgendwie bestimmen.

4.464

Die Wahrheit der Tautologie ist gewiss, des Satzes möglich, der Kontradiktion unmöglich. (Gewiss, möglich, unmöglich: Hier haben wir das Anzeichen jener Gradation, die wir in der Wahrscheinlichkeitslehre brauchen.)

4.465

Das logische Produkt einer Tautologie und eines Satzes sagt dasselbe, wie der Satz. Also ist jenes Produkt identisch mit dem Satz. Denn man kann das Wesentliche des Symbols nicht ändern, ohne seinen Sinn zu ändern.

4.466

Einer bestimmten logischen Verbindung von Zeichen entspricht eine bestimmte logische Verbindung ihrer Bedeutungen; jede beliebige Verbindung entspricht nur den unverbundenen Zeichen. Das heisst, Sätze die für jede Sachlage wahr sind, können überhaupt keine Zeichenverbindungen sein, denn sonst könnten ihnen nur bestimmte Verbindungen von Gegenständen entsprechen. (Und keiner logischen Verbindung entspricht keine Verbindung der Gegenstände.) Tautologie und Kontradiktion sind die Grenzfälle der Zeichenverbindung, nämlich ihre Auflösung.

4.4661

Freilich sind auch in der Tautologie und Kontradiktion die Zeichen noch mit einander verbunden, d. h. sie stehen in Beziehungen zu einander, aber diese Beziehungen sind bedeutungslos, dem Symbol unwesentlich.

4.5

Nun scheint es möglich zu sein, die allgemeinste Satzform anzugeben: das heisst, eine Beschreibung der Sätze irgendeiner Zeichensprache zu geben, so dass jeder mögliche Sinn durch ein Symbol, auf welches die Beschreibung passt, ausgedrückt werden kann, und dass jedes Symbol, worauf die Beschreibung passt, einen Sinn ausdrücken kann, wenn die Bedeutungen der Namen entsprechend gewählt werden. Es ist klar, dass bei der Beschreibung der allgemeinsten Satzform nur ihr Wesentliches beschrieben werden darf, – sonst wäre sie nämlich nicht die allgemeinste. Dass es eine allgemeine Satzform gibt, wird dadurch bewiesen, dass es keinen Satz geben darf, dessen Form man nicht hätte voraussehen (d. h. konstruieren) können. Die allgemeine Form des Satzes ist: Es verhält sich so und so.

4.51

Angenommen, mir wären alle Elementarsätze gegeben: Dann lässt sich einfach fragen: welche Sätze kann ich aus ihnen bilden. Und das sind alle Sätze und so sind sie begrenzt.

4.52

Die Sätze sind Alles, was aus der Gesamtheit aller Elementarsätze folgt (natürlich auch daraus, dass es die Gesamtheit aller ist). (So könnte man in gewissem Sinne sagen, dass alle Sätze Verallgemeinerungen der Elementarsätze sind.)

4.53

Die allgemeine Satzform ist eine Variable.