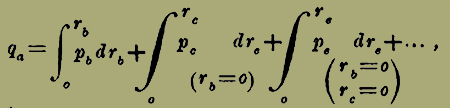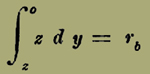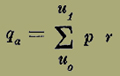Considerazioni sui principii fondamentali

dell'economia politica pura

1892

______________________________________________________________________________

[485]

Teorema fondamentale della trasformazione di un numero qualsivoglia di beni. Supponiamo, col Prof. Edgeworth, che i motivi i quali fanno sì che un individuo trasformi l'uno nell'altro due beni economici dipendano esclusivamente dalle quantità di quei beni che egli possiede. Abbiamo veduto che egli seguiterà la trasformazione sinchè questa più a lui non rechi alcun utile, il che corrisponde al massimo di utilità totale che può ricavare da quei beni economici mediante la trasformazione.

Questo teorema ha evidentemente valore qualunque numero di beni economici si consideri.

Vi sarebbe, rigorosamente, da tenere conto della ragione di trasformazione (del prezzo) di una merce qualunque paragonata con tutte le altre, ma giova sino da principio assumere una comune misura, cioè una moneta  ¹⁾, ed allora [486] le ragioni di trasformazione (i prezzi) sono solo in numero eguale a quello dei beni economici, anzi a quel numero meno uno se, come faremo, si usa uno di quei beni come moneta.

Quei prezzi sono dallo Jevons e dal Prof. Walras ritenuti costanti per l'intera quantità trasformata, ma dal Prof. Edgeworth e dal Prof. Marshall sono considerati anche variabili per le successive parti di beni trasformati.

P = Utilità totale ricavata dal consumo di quelle quantità di beni.

e sono solo funzioni di una variabile ciascuno, mentre i precedenti possono contenere tutte le variabili.

Perchè l'individuo che possiede quei beni non compia più alcuna trasformazione, ossia perchè quelle quantità sieno quelle che corrispondono allo stato di equilibrio, occorre [487] che l'utilità di una trasformazione infinitesima qualunque sia zero.

uno di questi due accresci meoti dovrà essere negativo poichè una merce trasformandosi nell'altra, la quantità dell'una cresce se quella dell'altra scema. Poichè pb è la ragione di trasformazione sarà

∂r_a + p_b∂r_b = 0,

e quindi  ³⁾

(1)    p_b = – ∂r_a/∂r_b

L'utilità di questa trasformazione deve essere zero, e perciò:

(2)    ∂P/∂r_a · ∂r_a + ∂P/∂r_b · ∂r_b = 0,

ossia

∂P/∂r_a = 1/p_b · ∂P/∂r_b;

e similmente si avrebbero le altre equazioni del sistema seguente

(3)    ∂P/∂r_a = 1/p_b · ∂P/∂r_a = 1/p_c · ∂P/∂r_c = . . . . . .

Secondo lo Jevons e il Walras il grado finale di utilità di A è funzione solo di r_b, quello di B è funzione solo di r_b, e si ha

(4)    φ_a(r_a) = 1/p_b · φ_b (r_b) = 1/p_c · φ_c (r_c) = . . . .

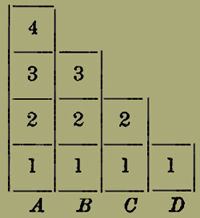
Da queste formolo nascono molte ed importanti illazioni, onde ci fermeremo un poco per ragionarne. E in prima vediamo come si esprimerebbero col linguaggio usuale.

Le formole (3) e (4) corrispondono al teorema del Gossen o dello Jevons sui gradi finali di utilità: In qualsiasi momento in cui i mezzi disponibili sì esauriscono, [488] i bisogni che sono stati con essi soddisfatti hanno tutti eguali gradi di intensità, e questi sono i maggiori che nel dato momento l'individuo risenta  ⁴⁾.

Sì può con uno specchio dare forma più concreta al teorema.

I successivi quadrati della colonna verticale A rappresentano porzioni eguali, e di eguale prezzo, per esempio del prezzo di una lira, della merce A. I quadrati in cui è partita la colonna B figurano altresì porzioni successive della merce B, ciascuna delle quali ha il prezzo fissato precedentemente, cioè una lira.

Similmente i quadrati delle colonne C, D . . . . rappresentano porzioni delle merci C, D, . . . . tutte al prezzo di una lira. Si suppone inoltre che i numeri scritti in quei quadrati dimostrino l'utilità per l'individuo delle porzioni di merce che rappresentano.

Questo specchio è fatto un poco artificialmente, per comodo delle dimostrazioni. Sul come le ipotesi in esso tacitamente ammesse concordino coi fatti veggasi il paragrafo: Varietà degli umani bisogni, di questo stesso capitolo.

Ora ragionando su quello specchio appare evidente che chi ha una sola lira da spendere compra la merce del quadrato 4 (A). Chi ha tre lire da spendere compra inoltre le merci dei quadrati 3 (A) e 3 (B), e cosi via via, chi ha [489] 10 lire da spendere compra 4 (A), 3 (A), 3 (B) – 2 (A), 2 (B), 2 (C) – 1 (A) 1 (B) 1 (C) 1 (D). Ma se avesse solo 9 lire da spendere? Allora se le merci dei quadrati segnati 1 sono divisibili, dovrebbe comprarne 3/4 di ciascuna, poichè 3 lire è appunto ciò che gli avvanza dopo che ha soddisfatto ai bisogni più urgenti che corrispondono ai quadrati seguenti 2.

Di questo specchio si può anche dare un altra figura ⁵⁾.

Fig. 2.

Si supponga che in un masso solido si sieno fatti tanti fori verticali o pozzetti, A, B, C . . . ., comunicanti fra di loro, e variamente profondi. Vi si versi dentro una certa quantità d'acqua la quale si disporrà ad un livello XY. La profondità h alla quale si trova la fotta uv sia proporzionale all'intensità del bisogno soddisfatto dalla porzione di merce figurata da quella fetta. Avremo allora l'imagine della ripartizione di una certa quantità di beni disponibili per comprare alcune merci. E si può anche tenere conto che le merci non sono indefinitamente divisibili supponendo di versare rena invece di acqua nei pozzetti; saranno riempiti solo quelli assai larghi per lasciare passare un granellino di rena, quelli più stretti rimarranno vuoti.

Il Wicksteed ha dato con molta lucidità la spiegazione pratica del teorema. Egli dice: ⁶⁾ «In egual modo il padre [490] di famiglia, o la buona massaia procura di fare sì che l'ultimo soldo (scellino, sterlina, o qualunque sia in ciascun caso particolare la minore somma sensibile) spesa in ciascun bene produca la stessa utilità o lo stesso piacere. Se questo scopo non è raggiunto, il denaro non è speso colla maggiore convenienza. Ma come si raggiunge questo scopo? Evidentemente col regolare gli acquisti di ciascuna merce in modo che il grado finale di utilità (marginal utilities) di quella quantità che si può avere per un soldo sia eguale per ciascuna merce».

Grado finale di utilità dei beni instrumentali. È necessario porre mente che i gradi finali di utilità di cui si discorre sono esclusivamente quelli di merci che si consumano. Se si tratta di un bene economico che non si gode direttamente, ma che serve solo a procacciare altri beni economici che si consumano, ossia se si tratta di un bene che è unicamente instrumentale, questo non ha un proprio grado finale di utilità che possa figurare nelle formole che abbiamo esposte, ma il suo grado di utilità è eguale semplicemente al comune valore dei gradi di utilità dei beni che con esso si ottiene.

Consideriamo infatti un individuo che possieda grano e che, recatosi al mercato, lo baratti con vino. Di questo egli non beve nè punto nè poco, ma se ne serve per acquistare olio, carne, legumi. Allora l'utilità per tale individuo di un litro di vino è solo quella dell'olio, della carne, dei legumi con cui può barattarlo. Vi è dunque questa differenza essenziale tra l'utilità del vino che si beve e quella del vino che serve ad acquistare altre merci, che la prima è determinata per l'individuo che si considera, e la seconda rimane per esso indeterminata sinchè non conosce le proporzioni (i prezzi) colle quali può barattare quel vino con olio, carne e legumi.

Teorema. – Il grado finale di utilità dei beni instrumentali è variabile coi prezzi delle merci che si consumano e colle altre condizioni del mercato, salvo casi singolarissimi. [491] Quindi quel grado finale di utilità non si può mai, teoricamente, assumere come costante.

L'importanza di questo teorema ci consiglia a darne diverse dimostrazioni. Le prime, dove non si usa la matematica sono imperfette, e debbonsi riguardare piuttosto come spiegazioni che come vere dimostrazioni.

I. Torniamo allo specchio precedentemente esposto. Suppongasi che le merci figurate dai diversi quadretti si ottengano mediante il baratto con un bene instrumentale, che non si consuma direttamente. Allora se abbiamo un unità di quel bene acquisteremo la merce del quadretto 4, e il grado di utilità di quell'unità di bene instrumentale è precisamente 4.

Se abbiamo tre unità di questo bene acquisteremo le merci dei tre quadretti 4-3-3. L'utilità dell'ultima porzione del bene instrumentale non è altro che 1'utilità della merce che si acquista con quelle porzioni, cioè 3. E così di seguito si vedrà che il grado di utilità finale del bene instrumentale, quando ne abbiamo 10 unità, è 1, poichè 1 è l'utilità della merce che si acquista con 1'ultima porzione di quel bene, e poichè è supposto che non serva ad altro. E se invece di 10 unità se ne avessero 9, supposto che le merci degli ultimi quadretti fossero divisibili, il grado finale di utilità del bene instrumentale sarebbe 3/4.

Quel grado di utilità varia dunque col variare della quantità posseduta, e quindi non si può assumere costante.

Inoltre supponendo che per una scoperta, un perfezionamento dell'industria, insomma per qualsivoglia cagione, sia portato sul mercato una nuova merce di cui con una unità del bene istrumentale si può acquistare una porzione avente l'utilità 1, cresce un quadretto nell'ultima linea orizzontale dello specchio, e il grado finale di utilità del bene instrumentale, di cui abbiamo 10 unità e che era 1 prima che comparisse la nuova merce, è ridotto a 4/5, poichè ripartiremo le ultime 4 unità acquistando 4/5 della merce di ciascun quadretto 1. [492]

Infine se varia il prezzo della merce D, ad esempio, per modo che la quantità più piccola che si può acquistare con un unità dei bene instrumentale sia 2, invece di 1; allora cresce un quadretto della penultima linea orizzontale, e non rimangono più che 3 unità del bene instrumentale per acquistare le merci dei quattro quadretti 1, il grado finale di utilità è dunque 3/4.

Concludiamo che qualsiasi variazioni delle condizioni del mercato fa variare il grado finale di utilità di una stessa quantità del bene instrumentale.

II. Il teorema prende forma concreta mediante le considerazioni spiegate nella Fig. 2.

L'acqua che si versa nei pozzetti figura il bene instrumentale mercè del quale acquistiamo i beni pel diretto consumo rappresentati dalle parti piene dei pozzetti. Poiché quel bene instrumentale non ha utilità propria, il suo grado finale di utilità è eguale a quello dell'ultima fetta X Y dei vari beni che con esso ci procuriamo. Quel grado finale di utilità è dunque figurato dall'altezza T.

Fig. 2.

Ora se si aprono nuovi pozzetti, se si chiude alcuno degli antichi, se si muta la profondità o la sezione di alcuno fra quelli che rimangono, con le quali cose tutte si rappresenta mutamenti dello stato del mercato, muta pure il livello X Y; ed in conseguenza muta il grado finale di utilità di quella quantità di bene instrumentale.

Non ci sarebbe che il caso singolarissimo, e pochissimo probabile, in cui tutti quei cambiamenti si compensassero l'uno l'altro per fare rimanere inalterato il livello X Y.

III. Se, come dicono lo Jevons e il Wicksteed, dobbiamo disporre del denaro che possediamo in modo che sia eguale il grado finale di utilità di tutte le merci che compriamo con gli ultimi soldi spesi, è manifesto che se quelle merci mutano di numero, di prezzo ecc., muterà pure il modo di disporre di quegli ultimi soldi, quindi muterà la loro utilità, che è il grado finale dì utilità della somma di moneta che spendiamo, considerata unicamente come bene instrumentale. [493]

IV. Supponiamo che A sia un bene instrumentale di cui la quantità

Prima supponiamo, col Prof. Walras, che quei prezzi sieno costanti per tutte le successive porzioni di una stessa merce, avremo

(5)    q_a = p_b r_b + p_c r_b + . . . .

Per fare uso delle formolo precedentemente scritte porremo

dr_a = – dq_a ;

poichè q_a scema quando r_b , r_c . . . . crescono.

Le equazioni (4) divengono

(6)    φ_a (q_a) = 1/p_b · φ_b (r_b) = 1/p_c · φ_c (r_c) = . . . .

Supponiamo, se è possibile, che il grado finale di utilità del bene instrumentale sia costante e eguale a m, avremo

φ_a (q_a) = m ,

e le formole precedenti ci permetteranno di calcolare r_b , r_c . . . in funzione di m e di p_b , p_c . . . ; potremo cioè scrivere

(7) r_b = ψ_b (m p_b)  ,  r_c = ψ_c (m p_c)  , . . .

Portando quei valori nell'equazione (5) si avrà:

q_a = p_b ψ_b (m p_b) + p_c ψ_c (m p_c) + . . .

e poichè p_b . . . sono indipendenti l'uno dopo dall'altro, non si potrà avere q_a costante che se si hanno pure costanti le quantità

p_b ψ_b (m p_b) , p_c ψ_c (m p_c) . . . . ;

ossia ricordando le equazioni (7) e se indichiamo con A_b , A_c . . . .

costanti, dovrà essere

(8)    p_b r_b = A_b , p_c r_c = A_c , . . . .

Si osservi che se q_a non fosse costante, vorrebbe dire che a determinati valori di m , p_b , p_c . . . corrisponde un determinato valore [494] di q_a ; e viceversa a vari valori di q_a , p_b , p_c . . . corrispondono vari valori di m, il che sarebbe contrario all'ipotesi che il grado d'utilità del bene instrumentale è costante.

Le equazioni precedenti combinate colle (6) danno

φ_b (r_b) = mp_b = mA_b/r_b , φ_c (r_c) = mA_c/r_c . . . .

Sicchè sarebbe necessario che i gradi finali di utilità di tutte le merci avessero quell'espressione singolarissima, perchè il grado finale di utilità di un bene istrumentale potesse rimanere costante. Tanto vale a dire che non lo sarà mai.

Si osservi che le condizioni (8) equivalgono a ritenere costante l'elasticità della domanda. Potremo dunque dire che, il grado finale di utilità di un bene instrumentale non può essere considerato costante, salvo il caso che tutte le merci che si acquistano con quel bene instrumentale abbiamo un elasticità della domanda costante.

Notisi che in questo caso si ha dalla formola (8) combinata colla (5) da

q_a = A_b + A_c + . . . ;

sicchè se compare qualche nuova merco sul mercato, o ne sparisce alcuna, varia qa; e perciò non basta neppure la condizione dell'elasticità della domanda costante, ma occorre per giunta che non muti il numero delle merci.

IV. ⁷⁾ Supponiamo coi Prof. Edgeworth; 1° che il grado finale di utilità di una merce sia funzione non della sola quantità di quella merce posseduta ma anche delle altre merci – 2° che il prezzo di una merce muti colle successive porzioni barattate.

Abbiamo

dq_a = ∂q_a/∂r_b · ∂r_b + ∂q_a/∂r_c · dr_c + . . . . ,    [495]

E coll'equazione (1), che per essere

dq_a = – dr_a ,

diventa

p_b = ∂q_a/∂r_b ,

otteniamo

(9)    dq_a = p_bdr_b + p_cdr_c + . . . . ;

p_b , p_c . . . sono funzioni note di r_b , r_c . . . .; e per farle variare indipendentemente da r_b , r_c , . . . introdurremo un parametro per ognuna di quelle funzioni ⁸⁾, scrivendo

p_b = f_b(r_b , r_c , . . . . u_b)

p_c = b_c(r_b , r_c , . . . . u_c)

L'equazione (9) integrata ⁹⁾ dà

ove l'espressione

p_c

(r_b = 0)

indica che in p_c sì deve far r_b = 0, e similmente per le altri simili espressioni.

Se l'utilità finale del bene istrumentale A, ossia se

∂P/∂r_a ,

è costante, occorre che a un dato valore di quella quantità corrisponda solo un determinato valore di q_a ; o in altre parole occorre che q_a non sia più funzione di u_b , u_c , . . . poichè altrimenti eliminando quelle quantità tra l'equazione trovata precedentemente e quelle (3) si [496] avrebbe una relazione ¹⁰⁾ ha il grado finale di utilità ∂P/∂r_a e q_a , il che è contrario all'ipotesi fatta.

Bisogna perciò che in q_a diamo a r_b , r_c . . . valore che che sieno funzioni di u_b , u_c . . . e tali da fare sparire queste ultime quantità.

Tranne dunque questo caso singolarissimo, il grado finale di utilità del bene instrumentale varierà colla quantità di esso.

Corollario. La moneta di metalli preziosi che usiamo avendo in sommo grado la qualità di bene istrumentale, il suo grado di utilità non può mai ammettersi teoricamente costante.

Per altro in molti casi si può approssimativamente ritenere tale.

Casi in cai il grado finale di utilità della moneta è all'incirca costante. Rigorosamente qualunque lievissima alterazione delle condizioni del mercato altera il grado finale di utilità della moneta, ma quest'alterazione può essere spesso trascurabile. Per esempio quando non è guari il governo italiano pensò bene per restaurare le finanze nazionali di accrescere il dazio sulle noci moscate, questo provvedimento rigorosamente parlando ha alterato il grado finale di utilità della moneta degli italiani, ma è evidente che quest'alterazione è insensibile, quasi quanto l'utile che no ha avuto l'erario. Invece il dazio sul grano imposto in Italia ha alterato considerevolmente il grano finale di utilità della moneta nel nostro paese. È dunque chiaro che vi sono alcuni fenomeni pei quali si può senza errore sensibile ritenere costante il grado finale di utilità della moneta, ed altri in cui invece quest'alterazione è la parte principale che conviene studiare.

A qualcuno forse parrà che abbiamo speso troppe parole per un quesito di cui la soluzione è evidente. E chi [497] non gradisce le teorie dell'Economia pura potrà anche scherzarci sopra, e dire; «C'era proprio bisogno di tirare fuori tante formole, gli specchi numerici, e anche i pozzetti! per farci sapere che, una lira, per chi ne ha poche, è più utile che per chi ne ha molte!».

Ma noi non abbiamo mai inteso di dare una dimostrazione di quel fatto, abbiamo mirato, ciò che è molto diverso, a darne un espressione rigorosa. Non sono le nostre formole che dimostrano il fatto, è invece il fatto che, col potere essere espresso dalle formole, accresce a queste autorità.

Del resto quest'obbiezione si potrebbe muovere ai principii di ogni scienza. Quasi sempre appaiono evidenti, ma è solo col darne espressione rigorosa che si può trarne le conseguenze.

★ Per esempio il principio delle velocità virtuali del Lagrangia in sostanza torna a dire che un corpo è in equilibrio quando non si muove in nessuna delle direzioni in cui potrebbe ciò fare. E sotto questa forma era forse conosciuto anche dagli uomini preistorici. Ma non si andava più in là. Invece sotto la forma rigorosa delle equazioni del Lagrangia racchiude tutta la Statica, e quando con essa si esprima il principio del D'Alembert, tutta la dinamica! Le non poche pagine, che i trattati di meccanica adoperano per spiegare e per fare intendere bene il principio del Lagrangia, sono dunque tutt'altro che inutili.

Giova poi aggiungere che se il principio della variabilità del grado finale di utilità della moneta è fra quelli che paiono evidenti, è anche fra quelli che più facilmente si dimenticarono in pratica.

Ne abbiamo veduto un esempio nell'esame fatto in un precedente articolo ¹¹⁾ della controversia tra il Prof. Walras e i Signori Auspitz e Lieben sulla teoria dei prezzi. Il punto saliente dell'argomento è appunto quello dell'utilità finale della moneta. [498]

Pensatamente in quell'articolo non abbiamo tenuto la via deduttiva, principiando a dimostrare la variabilità dell'utilità della moneta per poi trarne le conseguenze, ed invece abbiamo voluto procedere per via analitica. Abbiamo assunte in prima costante l'utilità finale della moneta, e sono i fatti che ci hanno costretto ad introdurre la condizione della sua variabilità.

A qualcuno questa via parrà forse meno scientifica, ma i seguaci del metodo sperimentale intenderanno perchè facciamo uso alternativamente dell'analisi e della sintesi, procurando, per modo di dire, di girare intorno all'argomento per considerarne tutti i lati. E anche dopo avere fatto ciò, sempre temiamo ci possa fuggire la verità, ma ben maggiore timore avremmo ove solo sotto un aspetto considerassimo il quesito.

Relazione tra il grado finale di utilità della moneta e la prosperità di un popolo. I prezzi delle merci sul mercato internazionale dipendono certamente del consumo di ciascun popolo, e magari anche di ciascun individuo. Ma si capisce facilmente che se un individuo mangia un pane di più del solito ciò non farà alzare il prezzo del grano. Similmente una differenza anche considerevole nel consumo di un solo popolo non muterà molto il prezzo del grano sul mercato mondiale.

Per le merci che si vendono sul mercato internazionale si possono dunque supporre i prezzi fissati secondo le circostanze generali, e allora si può dire che un popolo è tanto pia agiato quanto minore è il grado finale di utilità del suo oro.

Infatti un grado piccolo di utilità dell'oro, quando i prezzi sono fissi, indica piccoli gradi di utilità per tutte le merci, cioè quel popolo ha quasi a sazietà di ogni bene economico.

Se invece si tratta di merci che si contrattano solo su un mercato ristretto, allora i prezzi non si possono più assumere all'incirca costanti mentre varia il consumo, e un piccolo grado di utilità dell'oro può essere conseguenza [499] non già di un piccolo grado di utilità di quelle merci, ma bensì del fatto che il loro prezzo è molto cresciuto.

La proposizione ora enunciata è quella che il Cairnes espresse dicendo che «ciò a cui una nazione è interessata è, non ad avere i suoi prezzi alti o bassi, ma ad avere il suo oro a buon mercato, intendendo per buon mercato non un basso valore, ma un basso costo, cioè un piccolo sagrifizio di agio e di conforto» ¹²⁾. E spiega che «fra paesi commercialmente legati vi è una gran classe di mercanzie – tutte quelle cioè, che costituiscono i grandi cespiti del commercio, come il grano, la farina, il thè, lo zucchero, i metalli, e la maggiore parte dei materiali grezzi dell'industria – i prezzi dei quali non possono variare molto in differenti località. Come regola la differenza dei prezzi non sarà maggiore del costo di trasporto tra i paesi di produzione e di consumo, sempre s'intende eccettuando il caso in cui tali articoli vengano sotto l'azione delle leggi fiscali locali. Nello scambio contro mercanzie di questa specie, il valore dell'oro, quantunque non sia lo stesso in tutto il mondo, non varia grandemente entro la sfera del commercio internazionale. Ma oltre alle mercanzie che formano i cespiti del commercio, vi sono quelle che per non essere atte al traffico lontano, o per causa di qualche altro ostacolo non entrano nel commercio intemazionale. Per riguardo a queste non vi è nulla che impedisca la più larga divergenza nei loro prezzi in oro.....» ¹³⁾.

Tralasciando anche l'ambiguità di quelle parole «valore dell'oro» che non accresce chiarezza al ragionamento del Cairnes, non si può negare che il teorema non sia da lui enunciato e dimostrato in modo molto meno chiaro e rigoroso di quello che si può fare usando i principii dell'Economia razionale. E quand'anche questi avessero solo il pregio di accrescere rigore alle dimostrazioni, dovrebbero [500] sempre essere reputati di grande utilità nella scienza. Ma oltre questo maggiore rigore, la conoscenza precisa dei termini nei quali è vero il teorema gioverà per dedurne conseguenze.

Si potrebbe opporre che tutte queste considerazioni teoriche concludono poco nel concreto. Ed è vero che come non è per ignoranza dei precetti della morale che il malfattore si appropria la roba altrui, allo stesso modo non e solo per ignoranza delle verità della scienza economica che i politicanti sono tratti a male operare.

È manifesto che con costoro non giova nè la logica matematica, nè quella usuale, nè qualunque altra potesse l'uomo trovare; il linguaggio che intendono è di tutta altra fatta! Ma essi fanno loro prò dell'ignoranza del pubblico, e il togliere questa è il migliore, e forse l'unico mezzo, come dice il Molinari, per distruggere la loro potenza.

Veggasi per esempio ciò che segue per la moneta. I governi antichi e del medio evo l'alteravano mescolando metalli vili ai metalli preziosi. I politicanti moderni farebbero volontieri la stessa cosa, ma la maggiore coltura del pubblico li costringe di ricoprire con più sottile arte la stessa frode, e stampano carta moneta. Verrà giorno in cui, aumentando ancora la coltura popolare, neppure quell'inganno potrà più usarsi.

È naturale che il popolo non studierà mai la scienza economica, vi si usi o nò la matematica, ma non ha neanche avuto bisogna di studiare l'astronomia per liberarsi dai pregiudizi e dai timori cagionati altre volte dai fenomeni celesti, e bastò che alcuni dotti ne scoprissero le leggi. La pura teoria non è dunque inutile perchè solo da pochi può essere studiata, e se non direttamente, almeno indirettamente, accresce e migliora le popolari cognizioni.

La varietà degli umani bisogni. È notissima la legge della varietà degli umani bisogni che lo Jevons con ragione dice la più importante dell'Economia Politica, ed è pure noto che l'averla trascurata ha fatto nascere un numero grande di sofismi. [501]

Per scansare questi è necessario che introduciamo nelle nostre formole la condizione dei bisogni vari e crescenti degli uomini.

La matematica, col pregio grandissimo del rigore insuperabile della deduzione, accoppia un grave svantaggio, ed è che alcune volte condizioni alle quali non si pensava entrano furtivamente nelle formole. E da ciò segue che la scienza pare poi dare risposte che non sono a tono colle domande.

★ Esempii notissimi e puramente matematici sono quelli delle radici molteplici, e di quelle negative, o imaginarie, delle equazioni. Supponiamo un quesito che abbia evidentemente una sola soluzione; la chiediamo alla matematica, e viene fuori un'equazione con più radici! Ma questo accade perche nel porre il problema in equazione abbiamo, senza avvedercene, considerato oltre al quesito che avevamo in mira, un altro più generale.

Per scansare il pericolo di false interpretazioni è dunque necessario di badare bene non solo a ciò che poniamo nelle formole, ma anche a ciò che non vi facciamo entrare.

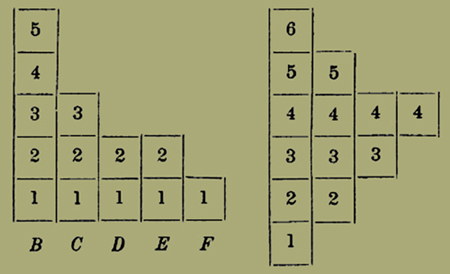
I.                                                       II.

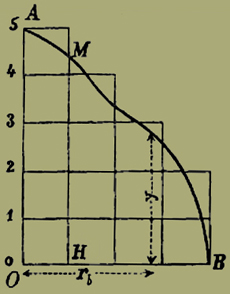
Lo specchio che figura la legge del Gossen ci mostra diversi fatti notevoli. Lasciando stare quello della decrescena dei gradi finali di utilità col crescere della quantità [502] della merce, sulla qual cosa dovremo a lungo discorrere in seguito, notiamo ora che man mano che scema il grado finale di utilità crescono di numero i quadretti, come si vede in I. Se invece la legge degli umani bisogni fosse quella che viene illustrata dalla figura II, l'Economia politica sarebbe interamente diversa dalla scienza che ora conosciamo con questo nome. Restringeremo dunque il nostro dire al caso della figura I. E ci proponiamo ora di dare una forma più rigorosa e più scientifica a quel modo di figurare il fenomeno.

Discontinuità del fenomeno. Principiamo col vedere come rimuovere una difficoltà che ci si para dinanzi sino dai primi passi.

Abbiamo supposto che i gradi di utilità decrescessero gradatamente, in modo che tutti gli ultimi quadretti fossero pieni; ma se la quantità della merce B che si compra con una lira, in vista di estinguere il bisogno 2, estinguesse non solo quel bisogno ma ancora ci saziasse interamente della merce, che accadrebbe? Sparirebbe il quadretto 1 – B, e allora che diventa il teorema che vuole eguali tutti gli ultimi gradi di utilità?

Queste difficoltà, che nascono dal dovere considerare funzioni discontinue, sono maggiori in Economia Politica che nelle scienze fisiche, perchè gli economisti solitamente non si sono preparati a trattare la materia con studi delle scienze matematiche ¹⁴⁾. Se l'Economia Politica diverrà una scienza matematica, sarà necessario che vengano pubblicati trattati ove chi studia Economia Politica possa facilmente trovare tutto quanto a lui occorre sapere di matematica e di meccanica ¹⁵⁾. [503]

E qui ci sia permessa una piccola digressione. La legge del Gossen non vale solo per l'economia politica, ma sarebbe utilissimo che se ne tenesse conto anche per l'istruzione.

Il Bain ¹⁶⁾ senza far cenno di questa legge, che probabilmente non aveva in mente, mostra come ogni uomo abbia solo disponibile una certa somma di facoltà mentali per imparare, per cui occorre spenderla avvedutamente; e evidentemente il modo migliore di spenderla è quella in cui le ultime conoscenze acquisite hanno tutte lo stesso grado di utilità per l'individuo. Ciò ora non ci fa quasi mai, e il giorno in cui si sarà trovato il modo di compiere tale opera, l'efficacia del lavoro intellettuale umano crescerà in modo forse maggiore di qualunque ardita ipotesi potessimo fare al presente.

L'obbiezione che si muove – vedasi tra gli altri il Block – all'uso della matematica, dicendo che non è nota al maggiore numero degli economisti, potrebbe quindi facilmente essere rimossa, perchè molte altre delle loro conoscenze sono spinte a tale segno da avere grado di utilità assai piccolo, per cui, restringendole, rimarrebbe tempo tanto quanto occorre per dare luogo allo studio alle scienze fisico-matematiche.

Ma torniamo al nostro problema. Nel concreto lo cose accadono come abbiamo supposto, e ben l'avvertiva il Wicksteed parlando del minimo sensibile, poichè non possiamo mai regolare le spese con tanta precisione da non avere saziato alcuni bisogni mentre altri rimangono.

Per tutte le persone ricche il grado finale di utilità del pane è zero. È impossibile che tolgano dalla spesa che fanno pel pane quel centesimo, o quella piccola frazione di centesimo, che sarebbe necessario per far nascere in loro un bisogno di mangiare pane eguale al bisogno che hanno di oggetti di lusso e superflui. [504]

Per rimuovere queste difficoltà si tiene generalmente il metodo di rendere continue le funzioni discontinue, assicurandosi contempora­neamente che l'errore commesso in tale guisa è trascurabile. Si è tratti a ciò fare da più motivi, uno fra i principali è che le funzioni discontinue sono molto più difficili a trattarsi, anche colla matematica, che non le funzioni continue.

★ Già abbiamo notato che la meccanica nel calcolo dell'attrazione Newtoniana, ed in altre congiunture, considera la materia come continua. E l'errore che ne nasce è assolutamente trascurabile.

Vediamo come seguendo questo idee potremo regolarci.

Le funzioni φ_b (r_b), φ_c (r_c) , . . . . delle formole (4) sieno continue, e rappresentiamo colla curva A la quantità

1/p_b · φ_b (r_b) ;

Ciò che veramente ci dice la legge del Gossen, c che è espresso dalle formolo (4), è che l'ascissa y che corrisponde all'ordinata r_b in questa curva

ò eguale all'ascissa y che corrisponde all'ordinata r_c nella curva

1/p_c · φ_c (r_c) ;

e cosi dì seguito per le altre curve.

Fig. 3.

Ma lo specchio esprime tutt'altro. Si è supposta divisa la linea AO della figura in 5 parti eguali, che sono proporzionali a φ_b (r_b), e quindi ai bisogni dell'individuo. Con l'unità di moneta si compra una quantità di merce B figurata da OH e si soddisfa ad un tempo il bisogno massimo OA e tutti quelli intermedi da OA ad HM. E non sarà che per un caso singolarissimo che HM si troverà per l'appunto eguale ai 4/5 di OA, come è supposto nello specchio. E nel fine della curva, in B, si vede come coll'ultima porzione comprata si sazia ad un tempo il bisogno 2, ed ogni altro bisogno sino a zero. [505]

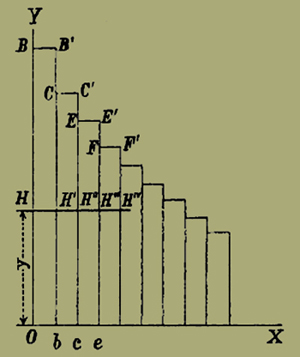
Fig. 4.

Tiriamo due rette perpendicolari OX e OY. Sull'asse delle ordinate OY porteremo lunghezze eguali ai gradi finali di utilità della moneta, cioè ai comuni valori di

1/p_b · φ_b (r_b) , 1/p_c · φ_c (r_c) , . . . .

Sull'asse OX porteremo i piccoli tratti

ob = p_b Δ u, bc = p_c Δ u, ce = p_e Δ u, . . . .

essendo u un parametro di cui sono funzione p_b , p_c , . . . r_b , r_c , . . . ; e Δ u essendo l'accrescimento di quel parametro quando si passa da una merce B ad un'altra C, da C ad E, ecc.

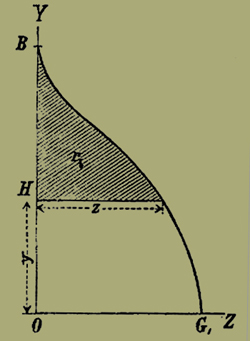
Tiriamo per OY un piano OYZ perpendicolare a quello del disegno. OZ sarà una retta che passa per O, ed è perpendicolare al piano del disegno, in modo che OX, OZ, OZ formano un sistema di tre assi ortogonali. Sìa OB la lunghezza che misura il grado finale di utilità della moneta quando r_b = 0. Muovendo dal punto B sognamo sul piano OYZ una curva BG, tale che la superfìcie compresa tra B e l'ordinata z, che corrisponde ad un valore qualunque del grado finale dì utilità della moneta, sia eguale a r_b .

Perciò si dovrà avere

e differenziando,

– z d y = d r_b .

Ma poichè

y = 1/p_b · φ_b(r_b) ,

Fig. 5.

viene

d y = 1/p_b · d r_b φ'_b(r_b) ;     [506]

e perciò

z = – p_b/φ'_b (r_b) .

Consideriamo una superficie cilindrica, generata da una retta parallela ad OX che si muove passando sempre per la curva BG. Il volume compreso tra questa superficie, il piano OXY, e i piani perpendicolari al piano OXY, che hanno per traccia HB, H'B', HH', è eguale a

r_b p_b Δ u,

poichè è una porzione di cilindro retto avente per base la superficie tratteggiata nella Fig. 5, e per altezza p_b Δ u.

Supponiamo che i bisogni sieno disposti io ordine decrescente di intensità. Allora b C sarà più piccolo di OB. Operando in modo simile a quello che abbiamo fatto ora, avremo in H'CC'H'' un volume eguale a

p_c r_c Δ u .

Seguitando si avrà una serie di fette cilindriche che formeranno il solido HH''''F'E'C'B'B, di cui il volume è

p_b r_b Δ u + p_c r_c Δ u + p_e r_c Δ u

Abbiamo supposto che u era un parametro tale che dando ad esso

Le funzioni p e r specialmente le prime, saranno per solito discon­tinue, cioè ad un piccolo accrescimento Δ u di u può corrispondere un accrescimento comunque sia grande di p, o di r.

Il volume del solido che ora abbiamo considerato si indicherà più semplicemente con

∑ p r Δ u

la somma estendendosi, nel caso della figura da uo sino a u_o + 3 Δ u, ed in generale da un certo valore u_o ad un altro valore u, il che si indica scrivendo

u1

∑ p r Δ u

u_o                        [507]

e l'equazione (5) diventa

Per esprimere le equazioni (4), che danno la legge del Gossen, colle nuove notazioni occorre introdurre una funzione φ che muti forma col mutare del valore di u, in modo che pei

F allora la legge di Gossen si esprime dicendo che l'espressione

1/p · φ (r)

deve rimanere costante variando u. Quel valore costante è il grado finale di utilità della moneta φ_a (q_a), e equazioni (4) sono sostituite da

φ_a (q_a) = 1/p · φ (r).

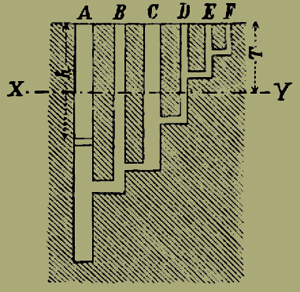
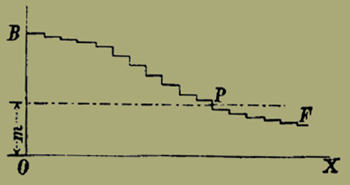
Si immagini ora scavato in un masso solido il volume indicato dalla fig. 5 capovolta, in modo cioè che il piano OXZ, che faremo orizzontale, sia quello superiore del masso. Allora se si versa in quell'incavo un volume eguale a q_a di acqua, la distanza y del suo livello dal piano orizzontale superiore ci indicherà il grado finale di utilità della moneta che corrisponde a quella quantità q_a, mentre il volume d'acqua contenuto in ciascuna delle fette cilindriche ci farà conoscere la spesa che si è fatta per soddisfare al bisogno figurato da quella fetta cilindrica.

Fig. 6.

La legge della varietà crescente dei bisogni umani è indicata dalla forma della linea BF, che si allunga indefinitamente pel verso OX. E il teorema ben noto che non vi può mai essere un eccesso generale di produzione, si traduce dicendo che mai il grado finale di utilità della moneta [508] può esser troppo piccolo, e si vede sulla figura che qualunque piccola utilità m abbia la moneta rimaranno sempre i bisogni PF . . . . da soddisfare.

Quando si considera un numero grande di bisogni, si può sostituire con lieve errore, una curva continua alla linea spezzata BPF. . .

In questo modo si sarebbe ottenuta la continuità tanto per le quantità di beni che soddisfano ogni bisogno, come pei bisogni stessi; il che era lo scopo che ci eravamo prefissi.

Possiamo seguitare, e cercare anche di ottenere la continuità nel considerare i diversi individui. È manifesto che quando vogliamo studiare l'economia politica di un popolo intero, quando cioè studiamo l'economia di parecchi milioni di individui, non possiamo tener conto delle differenze individuali se non in quanto sovrapponendosi i loro effetti contribuiscono al fenomeno generale.

Per tenere conto delle variazioni da un individuo all'altro del grado finale di utilità introdurremo un nuovo parametro v. E quindi la funzione

φ(r, u, v)

figurerà e compendierà la società che si studia.

E forse verrà giorno in cui potremo avere un'idea della forma di quella funzione per le nostre società, e dal confronto dei suoi valori in varie epoche potremo trarre preziosi ammaestramenti. Oggi che tale cognizione ancora ci è negata, non è per altro interamente inutile porre mente a quelle funzioni, poichè possiamo mercè di esse figurare società ideali e trarre conclusioni, che paragonate ai fatti reali potranno insegnarci quanto si discostino dalla verità le nostre ipotesi, e quindi farci strada ad introdurvi opportune modificazioni.

Grado finale di utilità dei beni ìnstrumentali di vari ordini. Il Menger dice: «il nostro benessere è assicurato quando siamo in possesso di beni atti alla immediata soddisfazione dei nostri bisogni. Questa categoria di beni la [509] chiameremo per brevità « beni di primo ordine». In essi il rapporto causale fra beni e soddisfazione di bisogno è immediato. Accanto si hanno beni per lor stessi incapaci di soddisfare direttamente un bisogno, ma capaci ad essere trasformati in beni di primo ordine. Il loro rapporto causale con la soddisfazione dei bisogni umani è mediato. Sono detti « beni di secondo grado». Similmente si possono avere beni di terzo e di quarto grado. Il lavoro del mugnaio che prepara la farina sarebbe di terzo grado, e il lavoro dell'agricoltore di quarto, e via dicendo».

Il grado finale di utilità di tutti quei beni istrumentali, secondo il teorema che abbiamo dimostrato, non può che essere preso eguale ai gradi finali di utilità dei beni di primo grado in cui si trasformano.

La cosa è vera, ed è utilissima a tenersi presente in alcune circostanze per distruggere molti sofismi che ingombrano la scienza economica, ma non si può negare che per quella via, quando vogliamo conoscere veramente quei gradi finali di utilità, siamo portati in un ginepraio cotanto intricato da non sapere più come cavarne i piedi.

Sia da investigare l'utilità di lamiere di ferro prodotte in Inghiltera. Quelle lamiere saranno comprate da un costruttore di navi. La nave andrà in possesso di un armatore. Un negoziante noleggierà la nave e la caricherà di cotone. Quel cotone sarà filato a Manchester, i fili saranno portati in Italia, e se ne farà un tessuto, che finalmente, per voler esser brevi, capiterà in mano del consumatore. Il grado di utilità di quelle lamiere non è altro che il grado di utilità di quel tessuto e di altri simili oggetti di diretto consumo che saranno procurati per mezzo della nave!

Si comprende facilmente come al vedersi spinti in cosi folta selva molti resistano e rifiutino senz'altro le teorie dell'Economia Pura. Occorre, a parer nostro, diligentemente studiare ciò che di ragionevole vi è nelle loro obbiezioni, e farne gran conto, nè giova altezzosamente respingerle, come contrarie alla teoria; perchè la teoria che non sa piegarsi alla pratica, non solo è inutile, ma altresì nociva. [510] E per ciò non sapremmo abbastanza lodare il parco uso che ne fa il Marshall nel suo trattato, tenendo sempre la mente fìssa ai fatti concreti. Quando la teoria pura sarà cresciuta ed avrà acquistato maggiore forza, allora potrà pretendere altresì maggior parte nello studio della scienza economica.

★ I teoremi generali nella scienza economica, come quello che ridu­cono il grado finale di utilità di qualsiasi bene economico ai gradi di utilità dei beni che soddisfano al diretto consumo, somigliano molto ai teoremi generali della dinamica.

★ Per esempio è utilissima la conoscenza del principio della conser­vazione del movimento del centro di gravità. Supposto che nessun corpo celeste estraneo al sistema solare operi su questo, sappiamo che il moto del centro di gravità del sistema solare deve essere uniforme. Ma non basta per l'astronomia. Abbiamo anche bisogno di conoscere i movimenti dei corpi di cui si compone il sistema.

Per l'Economia politica non basta ridurre all'utilità dei beni di primo grado quelle di tutti gli altri, occorre anche conoscere come per vari gradi si fanno quelle riduzioni. E ciò corrisponde alla realtà. Colui che produce le lamiere non si cura di sapere l'utilità dell'individuo che adoprerà la stoffa di cotone, egli bada solo ai bisogni del costruttore di navi.

Dobbiamo quindi riconoscere che la libera concorrenza è un sistema di ottenere mediante tentativi la risoluzione dell'equazione che fa il grado finale di utilità dei beni di ordine superiore eguale ai gradi di utilità dei beni di primo ordine ¹⁷⁾.

Il costruttore di nave assume pel grado finale di utilità della sua nave una funzione che procura sia quanto più prossima al vero è possibile. Il negoziante fa lo stesso pel cotone che importa dall'America, il filatore pei filati che produce e via di seguito. [512]

Gli errori inevitabili che in questi computi si commettono sono l'origine principale delle crisi periodiche delle industrie e dei commerci.

Se gli armatori hanno sbagliato nel fissare i gradi di utilità delle navi, e li hanno assunti troppo alti, i noleggi rinvilieranno, e questo fatto potrà produrre una crise nell'industria della costruzione delle navi.

Quando questi fatti accadono ad un tempo per parecchie industrie fanno nascere la falsa credenza che vi sia un eccesso di produzione generale, mentre invece non vi e che un eccesso di produzione in quelle industrie, ed è la manifestazione concreta di un errore nei computi fatti per eguagliare l'utilità dei beni di ordine superiore a quelli di primo ordine.

Un eccesso generale di produzione è impossibile per cagione della forma che ha lo specchio dei bisogni, come abbiamo veduto precedentemente. Per quanto grande sia il totale della produzione, purchè sia ripartita proporzionalmente ai vari bisogni, sarà sempre eguale al consumo, anzi sotto quell'aspetto generico produzione e consumo sono due parole per indicare una stessa cosa. Invece possono differire assai ove si considerino per alcune delle parti in cui si divide il totale.

In questo modo vediamo che la teoria lungi dal rimanere sopraffatta dalle difficoltà incontrate, da queste trae spiegazioni di fatti riconosciuti veri dall'esperienza. Ed in ciò dobbiamo vedere un motivo, fra i migliori che si possono avere, di tenere per vera la teoria.

Analiticamente sieno beni di primo grado

indicati con                                        B , C , E, . . .

Un bene di secondo grado         A

Uno di terzo grado                  S

e conserviamo notazioni analoghe a quelle usate precedentemente.

Il grado finale di utilità di A sarà dato dall'equazione

φ_a (q_a) = 1/p_b · φ (r_b) = 1/p_c · φ_c (r_c) = . . .

e quello di S da

(11) 1/p_s · φ_s (q_s) = φ_a (r_a) ,

Ma se vogliamo studiare solo il fenomeno della trasformazione di S in A dovremo a

φ_a (r_a) ,

sostituisce un'altra funzione

ψ_a (r_a),

la quale nel concetto di chi acquista A dovrebbe essere eguale alla funzione φ_a ma in realtà non è. E la differenza ha ψ_a e φ_a agisce a guisa di una forza sovra un punto materiale, e fa oscillare i prezzi e le quantità barattate intorno alle posizioni centrali che si avrebbero dall'equazione (11).

(Continua).

Vilfredo Pareto.

――――――――

1) I francesi hanno la parola monnaie e quella numeraire. Si può di ciò giovarsi per volgere il primo nome ad indicare una vera moneta, come sarebbe quella fatta con metalli preziosi, e serbare il secondo nome per indicare una moneta ideata per comodo di computo. Ma poichè in italiano abbiamo solo la parola moneta, ponga mente il lettore che qui si adopera per indicare una comune misura dei prezzi, e non altrimenti. 

2)Questo scritto potendo capitare fra le mani di persone che non hanno gran pratica della matematica, chi, invece ben conosce questa scienza abbia pazienza e ci scusi se aggiungiamo alcune note a lui inutili.

Badisi qui che ∂P/∂r_a indica la derivata di P presa rispetto a r_a, supponendo che r_b , r_c . . . rimangano costanti. È dunque la ragione dell'accrescimento infinitesimo di P a quello di r_a, supposti che le altre quantità non varino. 

3) Poiché dra e drb sono di segno contrario, pb è positivo, come infatti deve essere. 

4) Pantaleoni, Principi di economia pura – Barbèra, Firenze, pag. 59. 

5) Pantaleoni, loc. cit pag. 191. 

6) Wicksteed, Alphabet of Economic Science – London, Macmillan, 1888, pag. 125. E prima lo Jevons, loc. cit. pag. 242: «La teoria rappresenta così il fatto che una persona distribisce la sua spesa per tale modo da uguagliare l'utilità degli incrementi finali in ciascun ramo di spesa.» 

7) Il lettore che non abbia presente le Mathematical Psychics del Prof. Edgeworth prima di leggere questo paragrafo potrebbe vedere quanto più lungi diciamo su quest'argomento. 

8) I parametri nelle funzioni seguenti sono u_b , u_c , . . . 

9) L'espressione data sopra per dq_a è il differenziale totale, cioè la variazione totale che prova q_a quando r_a, r_b . . . crescono di dr_a, dr_b. L'espressione che si scrive ora è quella che rappresenta una quantità avente quel differenziale totale. Il calcolo integrale insegna appunto come dedurre questa quantità dalla precedente. 

10) Le quantità u_b, u_c , . . . da eliminare sono n – 1, ed occorrono perciò n equazioni. E sono per l'appunto tante, cioè n – 1 le (3), e una che quella che dà il valore di q_a . 

11) Nel fascicolo di Marzo di questo giornale. 

12) Cairnes – Principii di Economia Politica – Traduzione italiana – Firenze, Barbèra, pag. 439. 

13) Cairnes – loc. cit. p. 437. 

14) Man mano che le scienze acquistano estensione diventa necessario farne trattati aventi determinati scopi. Per esempio ora il Sig. Boussinesq ha pubblicato un trattato dì Analisi infinitesimale in servizio delle persone che studiano la meccanica. 

15) Basterebbe un piccolo volume, come quello dei Principii di Economia Pura del Pantaleoni, per dare tutte le notizie di matematica necessarie ad un economista. Ed un altro volume, anche più piccolo, basterebbe per la meccanica. Ma per ora non ci sarebbero lettori, ed è quindi naturale che a nessun editore venga in mente di pubblicare libri che rimarrebbero nei suoi magazzini ad uso esclusivo delle tignuole e dei topi. 

16) Bain – L'Esprit et le corps – Bibliothèque scicntifique internationale – pag. 239 e seguenti. 

17) Il Prof. Walras ha introdotto pel primo questa idea nelle scienze, a proposito del baratto delle merci. Élements d'Economie Pure pag. 149.