| |
ΠΑΠΠΟΥ ΑΛΕΞΑΝΔΡΕΩΣ ΣΥΝΑΓΩΓΗΣ Ηʹ.
Περιέχει δὲ μηχανικὰ προβλήματα σύμμικτα ἀνθηρά.
1. Ἡ μηχανικὴ θεωρία, τέκνον Ἑρμόδωρε, πρὸς πολλὰ καὶ μεγάλα τῶι ἐν τῶι βίωι χρήσιμος ὑπάρχουσα πλείστης εἰκότως ἀποδοχῆς ἠξίωται πρὸς τῶν φιλοσόφων καὶ πᾶσι τοῖς ἀπὸ τῶν μαθημάτων περισπούδαστός ἐστιν, ἐπειδὴ σχεδὸν πρώτη τῆς περὶ τὴν ὕλην τῶν ἐν τῶι κόσμωι στοιχείων φυσιολογίας ἅπτεται. στάσεως γὰρ καὶ φορᾶς σωμάτων καὶ τῆς κατὰ τόπον κινήσεως ἐν τοῖς ὅλοις θεωρηματικὴ τυγχάνουσα τὰ μὲν κινούμενα κατὰ φύσιν αἰτιολογεῖ, τὰ δ' ἀναγκάζουσα παρὰ φύσιν ἔξω τῶν οἰκείων τόπων εἰς ἐναντίας κινήσεις μεθίστησιν ἐπιμηχανωμένη διὰ τῶν ἐξ αὐτῆς τῆς ὕλης ὑποπιπτόντων αὐτῆι θεωρημάτων. τῆς δὲ μηχανικῆς τὸ μὲν εἶναι λογικὸν τὸ δὲ χειρουργικὸν οἱ περὶ τὸν Ἥρωνα μηχανικοὶ λέγουσιν· καὶ τὸ μὲν λογικὸν συνεστάναι μέρος ἔκ τε γεωμετρίας καὶ ἀριθμητικῆς καὶ ἀστρονομίας καὶ τῶν φυσικῶν λόγων, τὸ δὲ χειρουργικὸν ἔκ τε χαλκευτικῆς καὶ οἰκοδομικῆς καὶ τεκτονικῆς καὶ ζωγραφικῆς καὶ τῆς ἐν τούτοις κατὰ χεῖρα ἀσκήσεως· τὸν μὲν οὖν ἐν ταῖς προειρημέναις ἐπιστήμαις ἐκ παιδὸς γενόμενον κἀν ταῖς προειρημέναις τέχναις ἕξιν εἰληφότα πρὸς δὲ τούτοις φύσιν εὐκίνητον ἔχοντα, κράτιστον ἔσεσθαι μηχανικῶν ἔργων εὑρετὴν καὶ ἀρχιτέκτονά φασιν. μὴ δυνατοῦ δ' ὄντος τὸν αὐτὸν μαθημάτων τε τοσούτων περιγενέσθαι καὶ μαθεῖν ἅμα τὰς προειρημένας τέχνας παραγγέλλουσι τῶι τὰ μηχανικὰ ἔργα μεταχειρίζεσθαι βουλομένωι χρῆσθαι ταῖς οἰκείαις τέχναις ὑποχειρίοις ἐν ταῖς παρ' ἕκαστα χρείαις.
2. Μάλιστα δὲ πάντων ἀναγκαιόταται τέχναι τυγχάνουσιν πρὸς τὴν τοῦ βίου χρείαν [μηχανικὴ προηγουμένη τῆς ἀρχιτεκτονικῆς] ἥ τε τῶν μαγγαναρίων, μηχανικῶν καὶ αὐτῶν κατὰ τοὺς ἀρχαίους λεγομένων (μεγάλα γὰρ οὗτοι βάρη διὰ μηχανῶν παρὰ φύσιν εἰς ὕψος ἀνάγουσιν ἐλάττονι δυνάμει κινοῦντες), καὶ ἡ τῶν ὀργανοποιῶν τῶν πρὸς τὸν πόλεμον ἀναγκαίων, καλουμένων δὲ καὶ αὐτῶν μηχανικῶν (βέλη γὰρ καὶ λίθινα καὶ σιδηρᾶ καὶ τὰ παραπλήσια τούτοις ἐξαποστέλλεται εἰς μακρὸν ὁδοῦ μῆκος τοῖς ὑπ' αὐτῶν γινομένοις ὀργάνοις καταπαλτικοῖς), πρὸς δὲ ταύταις ἡ τῶν ἰδίως πάλιν καλουμένων μηχανοποιῶν (ἐκ βάθους γὰρ πολλοῦ ὕδωρ εὐκολώτερον ἀνάγεται διὰ τῶν ἀντληματικῶν ὀργάνων ὧν αὐτοὶ κατασκευάζουσιν). καλοῦσι δὲ μηχανικοὺς οἱ παλαιοὶ καὶ τοὺς θαυμασιουργοὺς, ὧν οἱ μὲν διὰ πνευμάτων φιλοτεχνοῦσιν, ὡς Ἥρων πνευματικοῖς, οἱ δὲ διὰ νευρίων καὶ σπάρτων ἐμψύχων κινήσεις δοκοῦσι μιμεῖσθαι, ὡς Ἥρων αὐτομάτοις καὶ ζυγίοις, ἄλλοι δὲ διὰ τῶν ἐφ' ὕδατος ὀχουμένων, ὡς Ἀρχιμήδης ὀχουμένοις, ἢ τῶν δι' ὕδατος ὡρολογίων, ὡς Ἥρων ὑδρείοις, ἃ δὴ καὶ τῆι γνωμονικῆι θεωρίαι κοινωνοῦντα φαίνεται. μηχανικοὺς δὲ καλοῦσιν καὶ τοὺς τὰς σφαιροποιί̈ας [ποιεῖν] ἐπισταμένους, ὑφ' ὧν εἰκὼν τοῦ οὐρανοῦ κατασκευάζεται δι' ὁμαλῆς καὶ ἐγκυκλίου κινήσεως ὕδατος.
3. Πάντων δὲ τούτων τὴν αἰτίαν καὶ τὸν λόγον ἐπεγνωκέναι φασίν τινες τὸν Συρακόσιον Ἀρχιμήδη· μόνος γὰρ οὗτος ἐν τῶι καθ' ἡμᾶς βίωι ποικίληι πρὸς πάντα κέχρηται τῆι φύσει καὶ τῆι ἐπινοίαι, καθὼς καὶ Γεμῖνος ὁ μαθηματικὸς ἐν τῶι περὶ τῆς τῶν μαθημάτων τάξεώς φησιν. Κάρπος δὲ πού φησιν ὁ Ἀντιοχεὺς Ἀρχιμήδη τὸν Συρακόσιον ἓν μόνον βιβλίον συντεταχέναι μηχανικὸν τὸ κατὰ τὴν σφαιροποιί̈αν, τῶν δὲ ἄλλων οὐδὲν ἠξιωκέναι συντάξαι. καίτοι παρὰ τοῖς πολλοῖς ἐπὶ μηχανικῆι δοξασθεὶς καὶ μεγαλοφυής τις γενόμενος ὁ θαυμαστὸς ἐκεῖνος, ὥστε διαμεῖναι παρὰ πᾶσιν ἀνθρώποις ὑπερβαλλόντως ὑμνούμενος, τῶν τε προηγουμένων γεωμετρικῆς καὶ ἀριθμητικῆς ἐχομένων θεωρίας [καὶ] τὰ βραχύτατα δοκοῦντα εἶναι σπουδαίως συνέγραφεν· ὃς φαίνεται τὰς εἰρημένας ἐπιστήμας οὕτως ἀγαπήσας ὡς μηδὲν ἔξωθεν ὑπομένειν αὐταῖς ἐπεισάγειν. αὐτὸς δὲ Κάρπος καὶ ἄλλοι τινὲς συνεχρήσαντο γεωμετρίαι καὶ εἰς τέχνας τινὰς εὐλόγως· γεωμετρία γὰρ οὐδὲν βλάπτεται, σωματοποιεῖν πεφυκυῖα πολλὰς τέχνας, διὰ τοῦ συνεῖναι αὐταῖς [μήτηρ οὖν ὥσπερ οὖσα τεχνῶν οὐ βλάπτεται διὰ τοῦ φροντίζειν ὀργανικῆς καὶ ἀρχιτεκτονικῆς· οὐδὲ γὰρ διὰ τὸ συνεῖναι γεωμορίαι καὶ γνωμονικῆι καὶ μηχανικῆι καὶ σκηνογραφίαι βλάπτεταί τι], τοὐναντίον δὲ προάγουσα μὲν ταύτας φαίνεται, τιμωμένη δὲ καὶ κοσμουμένη δεόντως ὑπ' αὐτῶν.
4. Τοιαύτης δὲ τῆς μηχανικῆς ἐπιστήμης ὁμοῦ καὶ τέχνης ὑπαρχούσης καὶ εἰς τοσαῦτα μέρη διηιρημένης καλῶς ἔχειν ἐνόμισα τά τε λόγωι γεωμετρικῶι θεωρούμενα [καὶ ἀναγκαιότατα περὶ τὴν τῶν βαρῶν κίνησιν κείμενα δὲ] παρὰ τοῖς παλαιοῖς καὶ τὰ ὑφ' ἡμῶν εὐχρήστως ἀνευρημένα θεωρήματα συντομώτερον καὶ σαφέστερον ἀναγράψαι βελτίονί τε λόγωι τοῦ παρὰ τοῖς πρότερον ἀναγεγραμμένου συντάξαι, οἷον βάρους δοθέντος ὑπὸ δοθείσης [ὑποδοχῆς] ἀγομένου δυνάμεως ἐν τῶι παρὰ τὸν ὁρίζοντα ἐπιπέδωι, καὶ ἑτέρου ἐπιπέδου κεκλιμένου πρὸς τὸ ὑποκείμενον δοθεῖσαν γωνίαν ὑποτιθέντος, εὑρεῖν τὴν δύναμιν ὑφ' ὅσης ἀχθήσεται τὸ βάρος ἐν τῶι κεκλιμένωι ἐπιπέδωι (τοῦτο δὲ χρήσιμον τοῖς μηχανικοῖς μαγγαναρίοις· προσθέντες γὰρ τῆι εὑρεθείσηι δυνάμει ἑτέραν τινὰ δύναμιν ἀνδρῶν θαρσοῦντες ἀνάγουσιν τὸ βάρος), καὶ δύο δοθεισῶν εὐθειῶν ἀνίσων δύο μέσας ἀνάλογον εὑρεῖν ἐν συνεχεῖ ἀναλογίαι (διὰ γὰρ τοῦ θεωρήματος τούτου πᾶν τὸ δοθὲν στερεὸν σχῆμα κατὰ τὸν δοθέντα λόγον αὔξεταί τε καὶ μειοῦται), καὶ πῶς δυνατόν ἐστι τυμπάνου δοθέντος καὶ τοῦ πλήθους τῶν σκυταλῶν αὐτοῦ [δοθέντων ἢ ὀδόντων] παραθεῖναι αὐτῶι τύμπανον δοθὲν ἔχον τὸ πλῆθος τῶν ὀδόντων καὶ εὑρεῖν τὴν διάμετρον τοῦ παρατιθεμένου τυμπάνου (τοῦτο γὰρ χρήσιμον εἰς πολλὰ καὶ τῆι τῶν μηχανοποιῶν τέχνηι διὰ τὴν παράθεσιν τῶν σκυταλωτῶν τυμπάνων). ἕκαστον δὲ τούτων ἐν τῶι οἰκείωι τόπωι γενήσεται φανερὸν μετὰ καὶ ἄλλων χρησίμων ἀρχιτέκτονι καὶ μηχανικῶι, ἐὰν πρότερον τὰ συνέχοντα τὴν κεντροβαρικὴν πραγματείαν εἴπωμεν ἑξῆς.
5. Τί μὲν οὖν ἐστιν τὸ βαρὺ καὶ τὸ κοῦφον, καὶ τίς αἰτία τῆς ἄνω καὶ κάτω τοῖς σώμασι φορᾶς, καὶ αὐτό γε τὸ ἄνω καὶ κάτω τίνος ἐννοίας ἔχεται καὶ τίσιν ἀφώρισται πέρασιν, οὐδὲν δεῖ λέγεσθαι παρ' ἡμῶν τὸ νῦν, ἐπειδὴ περὶ τούτων ἐν τοῖς μαθηματικοῖς ὑπὸ τοῦ Πτολεμαίου δεδήλωται, τὸ δὲ κέντρον τοῦ βάρους ἐκάστου σώματος, ὃ τῆς κεντροβαρικῆς πραγματείας ἀρχὴ καὶ στοιχεῖόν ἐστιν, ἐξ ἧς καὶ τὰ λοιπὰ μέρη τῆς μηχανικῆς ἀνήρτηται, τί ποτ' ἐστὶν καὶ τί βούλεται λεκτέον· ἐκ τούτου γάρ, οἶμαι, καὶ τὰ λοιπὰ τῶν ἐν τῆι πραγματείαι θεωρουμένων ἔσται σαφῆ. λέγομεν δὲ κέντρον βάρους ἑκάστου σώματος εἶναι σημεῖόν τι κείμενον ἐντός, ἀφ' οὗ κατ' ἐπίνοιαν ἀρτηθὲν τὸ βάρος ἠρεμεῖ φερόμενον καὶ φυλάσσει τὴν ἐξ ἀρχῆς θέσιν [οὐ μὴ περιτρεπόμενον ἐν τῆι φορᾶι]. τοῦτο δὲ τὸ σημεῖον οὐ μόνον ἐν τοῖς τεταγμένοις ἀλλὰ κἀν τοῖς ἀτάκτως ἐσχηματισμένοις εὑρίσκεται σώμασιν ὑπάρχον, ἐφόδωι τινὶ θεωρούμενον τοιαύτηι.
6. αʹ. Ὑποκείσθω γὰρ ἐπίπεδον ὀρθὸν τὸ ΑΒΓΔ νεῦον εἰς τὸ τοῦ παντὸς κέντρον, ἐφ' ὃ καὶ τὰ βάρος ἔχοντα πάντα τὴν ῥοπὴν ἔχειν δοκεῖ, καὶ ἔστω ἡ ΑΒ εὐθεῖα παράλληλος τῶι ἐφ' οὗ βεβήκαμεν ἐπιπέδωι. ἐὰν δή τι τῶν βάρος ἐχόντων σωμάτων τιθῆται κατὰ τῆς ΑΒ εὐθείας οὕτως, ὥστε τετμῆσθαι πάντως ὑπὸ τοῦ ἐπιπέδου ἐκβαλλομένου, ἕξει ποτὲ θέσιν τοιαύτην, ὥστε μένειν ἀπερίτρεπτον καὶ μὴ ἀποπίπτειν. γενομένου δὲ τούτου ἐὰν νοηθῆι τὸ ΑΒΓΔ ἐπίπεδον ἐκβαλλόμενον, τεμεῖ τὸ ἐπικείμενον σῶμα εἰς ἰσόρροπα δύο μέρη, οἷον περὶ ἄρτημα τὸ ἐπίπεδον ἰσορροποῦντα. πάλιν δὴ τὸ βάρος μετατεθέν, ὥστε καθ' ἕτερον μέρος ψαύειν τῆς ΑΒ εὐθείας, ἕξει ποτὲ θέσιν περιτρεπόμενον ὥστε μένειν ἀφεθὲν καὶ μὴ ἀποπίπτειν. ἐὰν οὖν πάλιν νοηθῆι τὸ ΑΒΓΔ ἐπίπεδον ἐκβεβλημένον, εἰς ἰσορρο ποῦντα μέρη τεμεῖ τὸ βάρος καὶ συμπεσεῖται τῶι πρότερον εἰς ἰσόρροπα τέμνοντι τὸ αὐτὸ βάρος ἐπιπέδωι· εἰ γὰρ μὴ τεμεῖ, τὰ αὐτὰ μέρη καὶ ἰσόρροπα καὶ ἀνισόρροπα γενήσεται ἀλλήλοις, ὅπερ ἄτοπον.
7. βʹ. Τούτων δὴ προειρημένων νοείσθω πάλιν εὐθεῖα ἡ ΑΒ ὀρθὴ πρὸς τὸ ἐφ' οὗ βεβήκαμεν ἐπίπεδον, εἰς τὸ τοῦ παντὸς κέντρον δηλονότι νεύουσα, καὶ τὸ βάρος ὁμοίως ἐπὶ τοῦ Α σημείου τιθέσθω, οἷον ὑποθέματι τῆι ΑΒ εὐθείαι χρώμενον [στήσεται δήποτε κατὰ τοῦ Α σημείου ὥστε μένειν, εἴ γε δὴ καὶ ἐπὶ τοῦ δι' αὐτῆς ἐπιπέδου τὸ βάρος ἠρεμεῖν ἐδύνατο]. ἐὰν δὴ μένοντος αὐτοῦ ἐκβληθῆι ἡ ΑΒ εὐθεῖα, ἐναποληφθήσεταί τι μέρος αὐτῆς ἐν τῶι ὑποκειμένωι σχήματι. νοείσθω δὴ τοῦτο μένον, καὶ πάλιν καθ' ἕτερον μέρος ἐπικείσθω τῆι εὐθείαι τὸ βάρος ὥστε ἠρεμεῖν· λέγω δὴ ὅτι ἐκβληθεῖσα ἡ ΑΒ εὐθεῖα συμπεσεῖται τῆι πρότερον ἐναπειλημμένηι. εἰ γὰρ μὴ συμπεσεῖται, δυνήσεταί τινα δι' ἀμφοτέρων αὐτῶν ἐκβληθέντα ἐπίπεδα μὴ συμπεσεῖν ἀλλήλοις ἐντὸς τοῦ σχήματος, καὶ ἑκάτερον αὐτῶν [ἐφαρμοζόμενον τῶι διὰ τῆς ΑΒ ἐπιπέδωι] διελεῖν τὸ βάρος εἰς ἰσόρροπα καὶ ἀνισόρροπα τὰ αὐτὰ μέρη, ὅπερ ἄτοπον· συμπεσοῦνται ἄρα αἱ εἰρημέναι εὐθεῖαι ἐντὸς τοῦ σχήματος. ὁμοίως δὲ κἂν κατ' ἄλλας θέσεις τιθῆται τὸ βάρος ἐπὶ τοῦ Α σημείου ὥστε μένειν, ἐκβληθεῖσα ἡ ΑΒ συμπεσεῖται ταῖς πρότερον ἐναπειλημμέναις [ὁμοίως] εὐθείαις. ἐξ οὗ φανερὸν ὡς καθ' ἓν σημεῖον ἀλλήλας τεμοῦσιν αἱ τὸν εἰρημένον τρόπον ἐπινοούμεναι εὐθεῖαι· τὸ δὲ σημεῖον τοῦτο κέντρον τοῦ βάρους καλεῖται. καὶ φανερὸν ὅτι ἐκ τοῦ κέντρου κατ' ἐπίνοιαν τὸ βάρος ἀρτώμενον οὐ περιτραπήσεται, μενεῖ δὲ τὴν ἐξ ἀρχῆς φυλάσσον ἡντινοῦν θέσιν ἐν τῆι φορᾶι· πάντα γὰρ δι' αὐτοῦ ἐκβληθέντα ἐπίπεδα εἰς ἰσόρροπα μέρη διαιρεῖ τὸ βάρος, ὥστε μηδεμίαν αἰτίαν ἐπιδέχεσθαι περιτροπῆς [ἰσορρόπων αὐτοῦ κατὰ πᾶσαν θέσιν τῶν ἐφ' ἑκάτερα τοῦ σημείου γινομένων μερῶν].
8. Τὸ μὲν οὖν μάλιστα συνέχον τὴν κεντροβαρικὴν πραγματείαν τοῦτ' ἂν εἴη, μάθοις δ' ἂν τὰ μὲν στοιχειώδη ὄντα διὰ ταύτης δεικνύμενα τοῖς Ἀρχιμήδους περὶ ἰσορροπιῶν ἐντυχὼν καὶ τοῖς Ἥρωνος μηχανικοῖς, ὅσα δὲ μὴ γνώριμα τοῖς πολλοῖς γράψομεν ἐφεξῆς, οἷον τὰ τοιαῦτα.
9. γʹ. Ἔστω τρίγωνον τὸ ΑΒΓ, καὶ αἱ πλευραὶ αὐτοῦ εἰς τὸν αὐτὸν λόγον τεμνέσθωσαν τοῖς Η Θ Κ σημείοις, ὥστε εἶναι ὡς τὴν ΑΗ πρὸς ΗΒ, τὴν ΒΘ πρὸς ΘΓ καὶ τὴν ΓΚ πρὸς ΚΑ, καὶ ἐπεζεύχθωσαν αἱ ΗΘ ΘΚ ΚΗ· ὅτι τοῦ ΑΒΓ τριγώνου καὶ τοῦ ΗΘΚ τὸ αὐτὸ κέντρον τοῦ βάρους ἐστίν.
Τετμήσθωσαν γὰρ αἱ ΒΓ ΓΑ δίχα τοῖς Δ Ε, καὶ ἐπεζεύχθωσαν αἱ ΑΔ ΒΕ· τὸ Ζ ἄρα κέντρον βάρους ἐστὶν τοῦ ΑΒΓ τριγώνου. ἐὰν γὰρ τὸ τρίγωνον ἐπί τινος ὀρθοῦ ἐπιπέδου ἐπισταθῆι κατὰ τὴν ΑΔ εὐθεῖαν, ἐπ' οὐδέτερον μέρος ῥέψει τὸ τρίγωνον διὰ τὸ ἴσον εἶναι τὸ ΑΒΔ τρίγωνον τῶι ΑΓΔ τριγώνωι. ἐπισταθὲν δὲ ὁμοίως τὸ ΑΒΓ τρίγωνον κατὰ τὴν ΒΕ ἐπὶ τοῦ ὀρθοῦ ἐπιπέδου ἐπ' οὐδέτερον μέρος ῥέψει διὰ τὸ ἴσα εἶναι τὰ ΑΒΕ ΒΓΕ τρίγωνα. εἰ δὲ ἐφ' ἑκατέρας τῶν ΑΔ ΒΕ ἰσορροπεῖ τὸ τρίγωνον, τὸ ἄρα κοινὸν αὐτῶν σημεῖον τὸ Ζ κέντρον ἔσται τοῦ βάρους. [νοεῖν δὲ δεῖ τὸ Ζ, ὡς προείρηται, κείμενον ἐν μέσωι τοῦ ΑΒΓ τριγώνου ἰσοπαχοῦς τε καὶ ἰσοβαροῦς δηλονότι ὑποκειμένου.] καὶ φανερὸν ὅτι διπλασία ἐστὶν ἡ ΑΕ, οὕτως ἡ ΑΒ πρὸς ΔΕ καὶ ἡ ΒΖ πρὸς ΖΕ καὶ ἡ ΑΖ πρὸς ΖΔ διὰ τὸ ἰσογώνια εἶναι καὶ τὰ ΔΖΕ ΑΒΖ τρίγωνα καὶ τὰ ΓΔΕ ΑΒΓ. ἐπιζευχθεῖσα οὖν ἡ ΔΕ τεμνέτω τὴν ΘΚ κατὰ τὸ Λ. ἐπεὶ οὖν ὁ τῆς ΒΘ πρὸς ΘΓ λόγος συνῆπται ἔκ τε τοῦ τῆς ΘΒ πρὸς ΔΘ καὶ τοῦ τῆς ΔΘ πρὸς ΘΓ, καὶ ἔστιν συνθέντι ὡς ἡ ΒΓ πρὸς ΓΘ, ἡ ΓΑ πρὸς ΑΚ, καὶ τῶν ἡγουμένων τὰ ἡμίση ὡς ΓΔ πρὸς ΓΘ, ἡ ΕΑ πρὸς ΑΚ, καὶ ἀναστρέψαντι ὡς ἡ ΓΔ πρὸς ΔΘ, ἡ ΑΕ πρὸς ΕΚ, ἴση δὲ ἡ μὲν ΓΔ τῆι ΒΔ, ἡ δὲ ΑΕ τῆι ΓΕ, καὶ ὡς ἄρα ἡ ΒΔ πρὸς ΔΘ, ἡ ΓΕ πρὸς ΕΚ· συνθέντι ἄρα ὡς ἡ ΒΘ πρὸς ΘΔ, ἡ ΓΚ πρὸς ΚΕ· σύγκειται ἄρα καὶ ὁ τῆς ΑΗ πρὸς ΗΒ λόγος ἔκ τε τοῦ τῆς ΓΚ πρὸς ΚΕ καὶ τοῦ τῆς ΔΘ
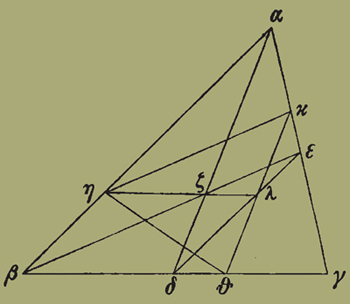
πρὸς ΘΓ. σύγκειται δ' ἐκ τῶν αὐτῶν καὶ ὁ τῆς ΔΛ πρὸς ΛΕ [καὶ ἴση ἐστὶν ἡ ΘΛ τῆι ΛΚ], ὡς δειχθήσεται· ἔστιν ἄρα καὶ ὡς ἡ ΑΗ πρὸς ΗΒ, ἡ ΔΛ πρὸς ΛΕ. καὶ εἰσὶν παράλληλοι αἱ ΑΒ ΔΕ, καὶ ἐπεζευγμέναι αἱ ΑΔ ΒΕ τέμνουσιν ἀλλήλας κατὰ τὸ Ζ· εὐθεῖα ἄρα ἐστὶν ἡ διὰ τῶν Η Ζ Λ· καὶ τοῦτο γὰρ ἑξῆς [εἰ μικρόν ἐστιν]. καὶ ἐπεί ἐστιν ὡς ἡ ΒΖ πρὸς ΖΕ, οὕτως ἡ ΗΖ πρὸς ΖΛ, διπλῆ δὲ ἡ ΒΖ τῆς ΖΕ, διπλῆ ἄρα καὶ ἡ ΗΖ τῆς ΖΛ. τριγώνου δὴ τοῦ ΗΘΚ διχοτομία ἡ ΗΛ, καὶ διπλῆ ἡ ΗΖ τῆς ΖΛ· τὸ Ζ ἄρα κέντρον βάρους ἐστὶν τοῦ ΗΘΚ τριγώνου. ἦν δὲ καὶ τοῦ ΑΒΓ.
10. δʹ. Τὸ δὲ ὑπερτεθὲν νῦν δειχθήσεται. ἔστω γὰρ ὡς ἡ ΓΔ πρὸς ΔΘ, ἡ ΓΕ πρὸς ΕΚ, καὶ ἐπεζεύχθωσαν αἱ ΔΕ ΘΚ τέμνουσαι ἀλλήλας κατὰ τὸ Λ· ὅτι ἴση μέν ἐστιν ἡ ΘΛ τῆι ΚΛ, ὁ δὲ τῆς ΔΛ πρὸς ΛΕ λόγος σύγκειται ἔκ τε τοῦ τῆς ΔΘ πρὸς ΘΓ καὶ τοῦ τῆς ΓΚ πρὸς ΚΕ.
Ἤχθω διὰ τοῦ Γ τῆι ΘΚ παράλληλος ἡ ΓΖ καὶ συμπιπτέτω τῆι ΔΕ ἐκβληθείσηι κατὰ τὸ Ζ. ἐπεὶ οὖν δύο εὐθεῖαί εἰσιν αἱ ΔΛ ΛΕ, καὶ ἔξωθεν ἡ ΖΛ, ὁ ἄρα τῆς ΔΛ πρὸς ΛΕ λόγος σύγκειται ἔκ τε τοῦ τῆς ΔΛ πρὸς ΛΖ καὶ τοῦ τῆς ΛΖ πρὸς ΕΛ. ἀλλὰ τῶι μὲν τῆς ΔΛ πρὸς ΛΖ λόγωι ὁ αὐτός ἐστιν ὁ τῆς ΔΘ πρὸς ΘΓ διὰ τὸ παράλληλον εἶναι τὴν ΓΖ τῆι ΚΘ, τῶι δὲ τῆς ΖΛ πρὸς ΛΕ λόγωι ὁ αὐτός ἐστιν ὁ τῆς ΓΚ πρὸς ΚΕ διὰ τὸ ἰσογώνια εἶναι τὰ ΓΕΖ ΕΚΛ τρίγωνα· καὶ ὁ τῆς ΔΛ ἄρα πρὸς τὴν ΛΕ λόγος σύγκειται ἔκ τε τοῦ τῆς ΔΘ πρὸς ΘΓ καὶ ἐκ τοῦ τῆς ΓΚ πρὸς ΚΕ. κατὰ ταὐτὰ δὴ δειχθήσεται ὅτι καὶ ὁ τῆς ΚΛ πρὸς ΛΘ λόγος συνῆπται ἔκ τε τοῦ τῆς ΚΕ πρὸς ΕΓ καὶ τοῦ τῆς ΓΔ πρὸς ΔΘ, παραλλήλου ἀχθείσης τῆι ΕΔ διὰ τοῦ Γ τῆς ΓΜ καὶ συμπιπτούσης τῆι ΚΘ ἐκβληθείσηι κατὰ τὸ Μ. ἐπεὶ γὰρ πάλιν δύο εὐθεῖαί εἰσιν αἱ ΚΛ ΛΘ ἔξωθεν τῆς ΛΜ λαμβανομένης, ὁ ἄρα τῆς ΚΛ πρὸς ΛΘ λόγος σύγκειται ἔκ τε τοῦ τῆς ΚΛ πρὸς ΛΜ καὶ τοῦ τῆς ΛΜ πρὸς ΛΘ. ἀλλ' ὁ μὲν τῆς ΚΛ πρὸς ΛΜ λόγος ὁ αὐτός ἐστιν τῶι τῆς ΚΕ πρὸς ΕΓ διὰ τὸ παράλληλον εἶναι πάλιν τὴν ΕΔ τῆι ΓΜ, ὁ δὲ τῆς ΛΜ πρὸς ΛΘ λόγος ὁ αὐτός ἐστιν τῶι τῆς ΓΔ πρὸς ΔΘ διὰ τὸ ἰσογώνια εἶναι τὰ ΔΘΛ ΓΘΜ τρίγωνα· ὁ ἄρα τῆς ΚΛ πρὸς ΛΘ λόγος ὁ αὐτός ἐστιν τῶι συγκειμένωι ἔκ τε τοῦ τῆς ΚΕ πρὸς ΕΓ, τουτέστιν τοῦ τῆς ΔΘ πρὸς ΔΓ, καὶ τοῦ τῆς ΓΔ πρὸς τὴν ΔΘ λόγου, ὃς τὸν τῆς ἰσότητος λόγον ποιεῖ· καὶ ὁ τῆς ΚΛ ἄρα πρὸς τὴν ΛΘ λόγος τῆς ἰσότητός ἐστιν· ἴση ἄρα ἡ ΚΛ τῆι ΛΘ.
11. εʹ. Τὸ λοιπὸν τῶν ὑπερτεθέντων. ἔστω παράλληλος ἡ ΑΒ τῆι ΓΔ, καὶ ὡς ἡ ΑΖ πρὸς ΖΒ, ἡ ΓΘ πρὸς ΘΔ, καὶ ἐπεζεύχθωσαν αἱ ΑΓ ΒΔ τέμνουσαι ἀλλήλας κατὰ τὸ Ε σημεῖον· ὅτι ἡ διὰ τῶν Ζ Ε Θ εὐθεῖά ἐστιν.
Εἰ γὰρ μή, ἔστω ἡ διὰ τῶν Ζ Ε Η. ἐπεὶ οὖν ἐστιν ὡς ἡ ΑΖ πρὸς
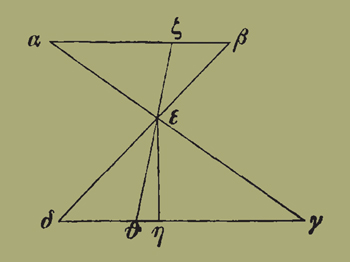
ΓΗ, οὕτως ἡ ΖΕ πρὸς ΕΗ, ὡς δὲ ἡ ΖΕ πρὸς ΕΗ, οὕτως ἡ ΖΒ πρὸς ΗΔ, ὡς ἄρα ἡ ΑΖ πρὸς ΓΗ, οὕτως ἡ ΖΒ πρὸς ΗΔ, καὶ ἐναλλὰξ ὡς ἡ ΑΖ πρὸς ΖΒ, τουτέστιν ὡς ἡ ΓΘ πρὸς ΘΔ, οὕτως ἡ ΓΗ πρὸς ΗΔ, ὅπερ ἀδύνατον· ἡ ἄρα διὰ τῶν Ζ Ε Θ σημείων εὐθεῖά ἐστιν.
12. ςʹ. Παραλληλογράμμου δοθέντος ὀρθογωνίου τοῦ ΑΓ, διαγαγεῖν τὴν ΓΔ ὥστε τοῦ ΑΒΓΔ τραπεζίου ἀρτηθέντος ἀπὸ τοῦ Δ τὰς ΑΔ ΒΓ παραλλήλους εἶναι τῶι ὁρίζοντι.
Γεγονέτω· ἡ ἄρα διὰ τοῦ Δ καὶ τοῦ κέντρου τοῦ βάρους τοῦ τραπεζίου ἀγομένη εὐθεῖα κάθετος ἔσται ἐπὶ τὸν ὁρίζοντα καὶ ἐπὶ τὴν ΒΓ. ἔστω ἡ ΔΛ, καὶ τετμήσθω δίχα ἡ ΔΛ κατὰ τὸ Ε, καὶ ἡ ΑΒ κατὰ τὸ Ζ, ἐπεζεύχθω δὲ ἡ ΓΕΖ, καὶ τετμήσθω ἡ ΓΕ κατὰ τὸ Θ ὥστε διπλῆν εἶναι τὴν ΓΘ τῆς ΘΕ, καὶ ἡ ΕΖ δίχα τετμήσθω κατὰ τὸ Η, καὶ ἐπεζεύχθω ἡ ΗΘ τέμνουσα τὴν ΔΛ κατὰ τὸ Κ· τὸ μὲν ἄρα Η κέντρον βάρους ἐστὶν τοῦ Β*δ παραλληλογράμμου, τὸ δὲ Θ κέντρον βάρους τοῦ ΓΔΛ τριγώνου· τοῦ ἄρα ὅλου τραπεζίου τὸ κέντρον τοῦ βάρους ἐπὶ τῆς ΗΘ ἐστίν. ἀλλὰ καὶ ἐπὶ τῆς ΔΛ· τὸ Κ ἄρα κέντρον βάρους ἐστὶν τοῦ ΑΒΓΔ τραπεζίου. ἀλλὰ καὶ τοῦ μὲν ΒΔ παραλληλογράμμου τὸ Η, τοῦ δὲ ΔΛΓ τριγώνου τὸ Θ· ἔστιν ἄρα ὡς τὸ ΒΔ παραλληλόγραμμον πρὸς τὸ ΔΓΛ τρίγωνον, οὕτως ἡ ΘΚ πρὸς τὴν ΚΗ. ἐὰν γὰρ ἀνὰ πεῖραν ἐπινοήσωμεν τοῦ μὲν ΒΔ παραλληλογράμμου [οὕτως ἔχον] τὸ βάρος ἐν ἑαυτῶι πᾶν συνῆχθαι πρὸς τῶι Η, τοὺ δὲ ΓΔΛ τριγώνου πᾶν τὸ βάρος ἐν τῶι Θ συνῆχθαι, γίνεται ὥσπερ ζυγὸς ἡ ΗΘ, ἐκ δὲ τῶν ἄκρων τὰ εἰρημένα βάρη. καὶ ἐὰν τμηθῆι ἡ ΗΘ κατὰ τὸ Κ, ὥστε εἶναι ὡς τὸ πρὸς τῶι Η βάρος πρὸς τὸ πρὸς τῶι Θ, τουτέστιν τὸ ΒΔ παραλληλόγραμμον πρὸς τὸ ΓΔΛ τρίγωνον, οὕτως τὴν ΘΚ εὐθεῖαν πρὸς τὴν ΚΗ κατὰ τὸν ἀντιπεπονθότα τῶν βαρῶν ἐν τοῖς ζυγοῖς λόγον, ἔσται τὸ Κ σημεῖον ἐξ οὗ τὰ βάρη ἰσορροπήσει [ὥστε καὶ τὸ ΑΒΓΔ ἐκ τοῦ Κ ἰσορροπήσει]. ἤχθωσαν δὴ κάθετοι ἀπὸ τῶν Η Θ ἐπὶ τὴν ΒΓ αἱ ΗΜ ΘΝ. ἐπεὶ οὖν ἐστιν ὡς τὸ ΒΔ παραλληλόγραμμον πρὸς τὸ ΓΔΛ τρίγωνον, οὕτως ἡ ΘΚ πρὸς τὴν ΚΗ, ἀλλ' ὡς τὸ παραλληλόγραμμον πρὸς τὸ τρίγωνον, οὕτως ἡ ΒΛ πρὸς τὴν ἡμίσειαν τῆς ΛΓ, ὡς δὲ ἡ ΚΘ πρὸς τὴν ΚΗ, οὕτως ἡ ΝΛ πρὸς τὴν ΛΜ διὰ τὸ εἰς παραλλήλους τὰς ΗΜ ΕΛ ΘΝ διῆχθαι τὰς ΗΚΘ ΜΛΝ, καὶ ὡς ἄρα ἡ ΒΛ πρὸς τὴν ἡμίσειαν τῆς Λ*γ, οὕτως ἡ ΝΛ πρὸς τὴν ΛΜ ἡμίσειαν οὖσαν τῆς ΒΛ· καὶ ὡς ἄρα ἡ ΒΛ πρὸς τὴν διπλασίαν, τουτέστιν πρὸς τὴν ΛΓ, οὕτως ἡ ΛΝ πρὸς τὴν διπλασίαν τῆς ΜΛ, τουτέστιν τὴν ΒΛ· τὸ ἄρα ἀπὸ τῆς ΒΛ ἴσον ἐστὶν τῶι ὑπὸ ΓΛΝ. [ἔστιν ἄρα ὡς μὲν ἡ ΓΛ πρὸς ΛΒ, ἡ ΒΛ πρὸς ΛΝ.] ὡς δὲ ἡ ΓΛ πρὸς ΛΝ, οὕτως τὸ ἀπὸ τῆς ΓΛ τετράγωνον πρὸς τὸ ἀπὸ τὴς ΒΛ τετράγωνον. καὶ τριπλῆ ἐστιν ἡ ΓΛ τῆς ΛΝ [ἐπεὶ καὶ ἡ ΓΕ τριπλῆ ἐστιν τῆς ΕΘ· διπλῆ γὰρ ἡ ΓΘ τῆς ΕΘ]· τριπλάσιον ἄρα τὸ ἀπὸ ΓΛ τοῦ ἀπὸ ΛΒ. καὶ δοθέντα τὰ Β Γ· δοθὲν ἄρα τὸ Λ, ὥστε καὶ τὸ Δ. διὸ δὴ τὴν ΒΓ τεμόντες κατὰ τὸ Λ, ὥστε τὸ ἀπὸ ΓΛ τοῦ ἀπὸ ΛΒ εἶναι τριπλάσιον, ἕξομεν τὸ Δ τῆς ἀρτήσεως σημεῖον. τέμνεται δὲ ἡ ΒΓ οὕτως.
13. ζʹ. Εὐθεῖαν τεμεῖν ὥστε τὴν μείζονα τῆς ἐλάττονος εἶναι δυνάμει τριπλασίαν.
Ἔστω εὐθεῖα ἡ ΑΔ καὶ τετμήσθω τῶι Γ, ὥστε τὴν ΑΓ τῆς ΓΔ εἶναι τριπλῆν, καὶ ἐπὶ τῆς ΑΔ γεγράφθω ἡμικύκλιον τὸ ΑΒΔ, καὶ πρὸς ὀρθὰς τῆι ΑΔ ἀπὸ τοῦ Γ ἡ ΓΒ, καὶ πεποιήσθω ὡς ἡ ΑΓ πρὸς ΓΒ, οὕτως ἡ ΑΕ πρὸς ΔΕ· ὅτι ἡ ΑΕ τῆς ΔΕ δυνάμει τριπλασία ἐστίν.
Ἐπεὶ γὰρ ἡ ΒΓ τῶν ΑΓ ΓΔ μέση ἀνάλογόν ἐστιν, ὡς ἄρα ἡ ΑΓ πρὸς τὴν ΓΔ, οὕτως τὸ ἀπὸ ΑΓ πρὸς τὸ ἀπὸ ΒΓ, τουτέστιν τὸ ἀπὸ ΑΕ πρὸς τὸ ἀπὸ ΔΕ· τριπλασία ἄρα ἡ ΑΕ τῆς ΔΕ δυνάμει.
Ὁμοίως καὶ εἰς τὸν δοθέντα λόγον δυνάμει τμηθήσεται ἡ ΑΔ εὐθεῖα καὶ πᾶσα ἡ δοθεῖσα εὐθεῖα.
14. ηʹ. Θέσει αἱ ΑΒ ΑΓ, καὶ δοθὲν τὸ Β, καὶ διήχθω ἡ ΓΔ ἀποτέμνουσα δοθέντα λόγον τὸν τῆς ΑΓ πρὸς ΒΔ· δεῖξαι ὅτι τοῦ ΑΓΔ τριγώνου τὸ κέντρον τοῦ βάρους ἐστὶ πρὸς θέσει.
Τετμήσθω ἡ ΑΓ δίχα τῶι Ε, καὶ ἐπιζευχθεῖσα ἡ ΔΕ τετμήσθω κατὰ τὸ Ζ, ὥστε τὴν ΕΖ τρίτον μέρος εἶναι τῆς ΕΔ· τὸ Ζ ἄρα
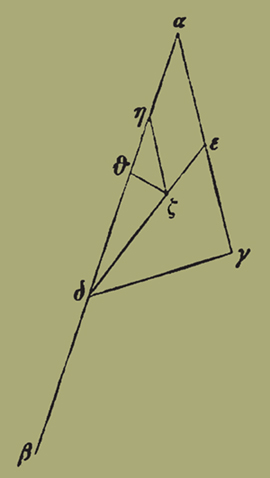
κέντρον βάρους ἐστὶν τοῦ ΑΓΔ τριγώνου [τοῦτο γὰρ προδέδεικται]. ἤχθω δὴ τῆι ΑΕ παράλληλος ἡ ΖΗ, καὶ τῆς ΑΒ τρίτον μέρος ἔστω ἡ ΑΘ. ἔστιν δὲ καὶ ἡ ΑΗ τρίτον μέρος τῆς ΑΔ, ἐπεὶ καὶ ἡ ΕΖ τῆς ΕΔ· καὶ λοιπὸν οὖν ἡ ΘΗ τρίτον μέρος ἐστὶν τῆς ΒΔ. λόγος δὲ τῆς ΒΔ πρὸς τὴν ΑΓ δοθείς [τῆς δὲ ΑΓ πρὸς τὴν ΖΗ· τριπλασία γὰρ αὐτῆς ἐστιν, ὅτι καὶ ἡ μὲν ΔΑ τῆς ΔΗ ἡμιολία ἐστίν, τουτέστιν ἡ ΑΕ τῆς ΖΗ, ἡ δὲ ΓΑ τῆς ΑΕ διπλῆ]· λόγος ἄρα καὶ τῆς ΗΘ πρὸς τῆν ΗΖ δοθείς. καὶ δοθεῖσα ἡ πρὸς τῶι Η γωνία [καὶ γὰρ ἡ πρὸς τῶι Α]· δοθεῖσα ἄρα καὶ ἡ ὑπὸ ΗΘΖ γωνία. καὶ δοθὲν τὸ Θ· θέσει ἄρα ἡ ΘΖ εὐθεῖα, καὶ ἔστιν ἐπ' αὐτῆς τὸ Ζ κέντρον.
15. Ταῦτα μὲν οὖν καὶ τὰ τοιαῦτα θεωρίαν ἔχει, τὰ δὲ καὶ εἰς χρείαν δυνάμενα πεσεῖν μηχανικὴν τοιαῦτ' ἂν εἴη.
θʹ. Ἐπίπεδον ἐκκλῖναι, ὥστε τὸ κλίμα αὐτοῦ ἐφ' ἓν νεύειν σημεῖον δοθέντος ἀκλινοῦς ἐπιπέδου, τουτέστιν παραλλήλου τῶι ὁρίζοντι, ἐν παραλληλογράμμωι, τὸ δὲ κλίμα ἔστω ἐν τῆι δοθείσηι γωνίαι.
Ἔστω τὸ δοθὲν παραλληλόγραμμον πρότερον ἰσόπλευρον τὸ ΑΒΓΔ, ἡ δὲ δοθεῖσα γωνία, ἐν ἧι βουλόμεθα ἐγκλῖναι τὸ ἐπίπεδον,
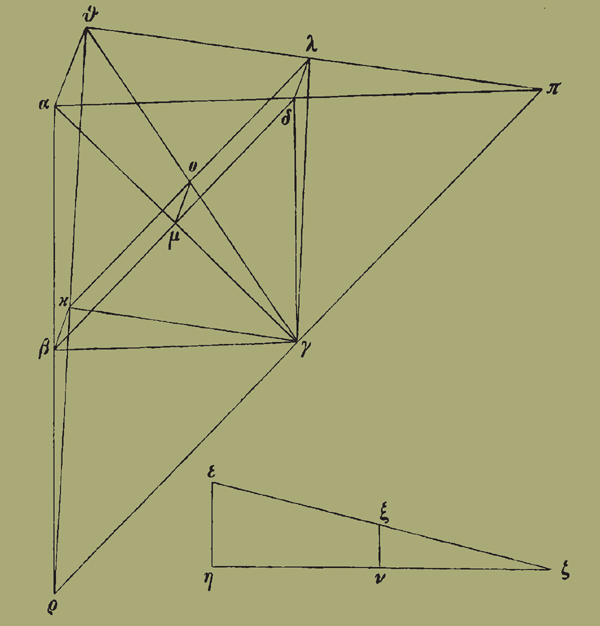
ἡ ὑπὸ ΕΖΗ, ἀπὸ δὲ τῶν Α Β Δ σημείων τῶι ὑποκειμένωι ἐπιπέδωι πρὸς ὀρθὰς ἀνεστάτωσαν αἱ ΑΘ ΒΚ ΔΛ, τὸ δὲ Γ σημεῖον ἔστω ὅπου βουλόμεθα τὴν κλίσιν νεύειν, καὶ τῆι μὲν ΑΓ ἐπιζευχθείσηι ἴση κείσθω ἡ ΖΗ, τῆι δὲ ΖΗ πρὸς ὀρθὰς ἤχθω ἡ ΕΗ, τῆι δὲ ΗΕ ἴση κείσθω ἡ ΑΘ. ἐὰν δὴ νοήσωμεν ἐπεζευγμένην τὴν ΘΓ, ἔσται ἡ ὑπὸ ΘΓΑ γωνία τῆς κλίσεως τῶν ἐπιπέδων. ἤχθω δὴ καὶ ἀπὸ τοῦ Β ἐπὶ τὴν ΑΓ κάθετος ἡ ΒΜ, καὶ τῆι ΓΜ ἴση κείσθω ἡ ΖΝ, τῆι δὲ ΖΗ πρὸς ὀρθὰς ἤχθω ἡ ΝΞ, τῆι δὲ ΝΞ ἴση κείσθω ἑκατέρα τῶν ΒΚ ΔΛ, καὶ ἐπιζευχθεῖσαι αἱ ΘΛ ΘΚ ἐκβεβλήσθωσαν καὶ συμπιπτέτωσαν ταῖς ΑΔ ΑΒ ἐκβληθείσαις κατὰ τὰ Π Ρ σημεῖα [ὅτι δὲ συμπίπτουσιν δῆλον· ἀπ' ἐλαττόνων γάρ εἰσιν δύο ὀρθῶν καὶ αὐταὶ κἀκεῖναι]· ἔσται δὴ τὸ ΘΚΛ ἐπίπεδον κεκλιμένον πρὸς τὸ ΑΒΓΔ ἐν τῆι ὑπὸ ΘΓΑ, τουτέστιν τῆι ὑπὸ ΕΖΗ. ἐὰν γὰρ νοήσωμεν τῆι ΑΘ παράλληλον ἠγμένην τὴν ΜΟ, καὶ ἐπεζευγμένην τὴν ΟΚ, ἔσται ἡ μὲν ΜΟ ἴση τῆι ΝΞ διὰ τὸ ἰσογώνιον εἶναι τὸ ΖΝΞ τρίγωνον τῶι ΜΟΓ, ἡ δὲ ΚΟ τῆι ΒΜ ἴση καὶ παράλληλος, καὶ παραλληλόγραμμον τὸ ΚΒΜΟ ὀρθὸν πρὸς ὑποκείμενον. καὶ ἐπεὶ τὰ Π Γ Ρ σημεῖα ἐν δυσὶν ἅμα ἐπιπέδοις ἐστὶν τῶι τε ὑποκειμένωι ΑΒΓΔ [ἐν ὧι ἐστιν καὶ τὰ Π Ρ σημεῖα, ἀλλὰ] καὶ ἐν τῶι ΚΘΛΓ, τὰ Π Γ Ρ ἄρα σημεῖα ἐπὶ μιᾶς ἐστιν εὐθείας τῆς ΠΓΡ, κοινῆς τομῆς οὔσης τῶν εἰρημένων ἐπιπέδων. διὰ ταὐτὰ δὴ καὶ τὰ Κ Ο Λ σημεῖα ἐπὶ τῆς κοινῆς ἐστι τομῆς τοῦ ΚΘΛΓ ἐπιπέδου καὶ τοῦ διὰ τῶν Κ Ο Λ παραλλήλου τῶι ΑΒΓΔ ἐπιπέδωι, ὥστε τὴν διὰ τῶν Κ Ο Λ εὐθεῖαν παράλληλον εἶναι τῆι ΠΡ. ἐπεὶ οὖν ἐστιν ὡς μὲν ἡ ΑΠ πρὸς ΠΔ, ἡ ΘΑ πρὸς ΛΔ, ὡς δὲ ἡ ΑΡ πρὸς ΡΒ, ἡ ΑΘ πρὸς ΒΚ, καὶ ἴση ἐστὶν ἡ ΔΛ τῆι ΒΚ, ἴση ἄρα καὶ ἡ ΑΠ τῆι ΑΡ καὶ γωνία ἡ ὑπὸ ΑΠΡ τῆι ὑπὸ ΑΡΠ. ἔστιν δὲ καὶ ἡ ὑπὸ ΠΑΓ ἴση τῆι ὑπὸ ΡΑΓ· λοιπὴ ἄρα ἡ ὑπὸ ΑΓΠ τῆι ὑπὸ ΑΓΡ· ὀρθὴ ἄρα ἐστὶν ἑκατέρα αὐτῶν, καὶ ἡ ΠΡ εὐθεῖα δίχα τε καὶ πρὸς ὀρθὰς τέμνεται ὑπὸ τῆς ΑΓ. καὶ ἔστιν αὐτῆι πρὸς ὀρθὰς καὶ τῶι ΑΒΓΔ ἐπιπέδωι ἡ ΜΟ· καὶ ἡ ΟΓ ἄρα πρὸς ὀρθάς ἐστιν τῆι ΡΠ διὰ λῆμμα σφαιρικῶν· ὀρθὴ ἄρα ἐστὶν ἑκατέρα τῶν ὑπὸ ΑΓΠ ΟΓΠ· τὸ ΚΘΛΓ ἄρα ἐπίπεδον κέκλιται πρὸς τὸ [ἀπὸ] ΑΒΓΔ ἐν τῆι δοθείσηι γωνίαι τῆι ὑπὸ ΕΖΗ.
16. Ἀλλὰ δὴ ἔστω μείζων ἡ ΑΒ τῆς ΑΔ, τῶν ἄλλων ὑποκειμένων τῶν αὐτῶν· λέγω ὅτι ἡ ὑπὸ ΑΓΠ ὀξεῖά ἐστιν.
Ἐπεὶ γάρ ἐστιν ὡς μὲν ἡ ΑΠ πρὸς ΠΔ, ἡ ΘΑ πρὸς ΔΛ, ὡς δὲ ἡ ΑΡ πρὸς ΡΒ, ἡ ΘΑ πρὸς ΒΚ, καὶ ἴση ἐστὶν ἡ ΔΛ τῆι ΒΚ, καὶ ὡς ἄρα ἡ ΑΠ πρὸς ΠΔ, ἡ ΑΡ πρὸς ΡΒ· καὶ διελόντι ἄρα ἐστὶν ὡς ἡ ΑΔ πρὸς ΔΠ, οὕτως ἡ ΑΒ πρὸς ΒΡ, καὶ ἐναλλὰξ ὡς ἡ ΑΔ πρὸς ΑΒ, οὕτως ἡ ΔΠ πρὸς ΒΡ. ἐλάττων δὲ ἡ ΑΔ τῆς ΑΒ· ἐλάττων ἄρα καὶ ἡ ΔΠ τῆς ΒΡ· ὅλη ἄρα ἡ ΑΠ ἐλάττων ἐστὶν τῆς ΑΡ, ὥστε καὶ γωνία ἡ ὑπὸ ΑΡΠ ἐλάσσων ἐστὶν τῆς ὑπὸ ΑΠΡ· μείζων ἄρα ἡ ὑπὸ ΑΠΡ τῆς ὑπὸ ΑΡΠ. ἔστιν δὲ καὶ ἡ ὑπὸ ΓΑΠ τῆς ὑπὸ ΓΑΡ μείζων· λοιπὴ ἄρα ἡ ὑπὸ ΑΓΠ τοῦ ΑΓΠ τριγώνου λοιπῆς τῆς ὑπὸ ΑΓΡ τοῦ ΑΓΡ τριγώνου ἐλάσσων ἐστίν· ὀξεῖα ἄρα ἡ ὑπὸ ΑΓΠ γωνία· ἡ κλίσις ἄρα τῶν εἰρημένων ἐπιπέδων πρός τι σημεῖον μεταξὺ τῶν Γ Π θεωρεῖται, ἀπὸ τοῦ Α σημείου ἐπὶ τὴν ΓΠ καθέτου ἀγομένης. ὡς οὖν ἐκκλῖναι δυνατόν ἐστιν ἐπίπεδον ἐν τῆι δοθείσηι γωνία πρὸς ἐπίπεδον, δυνατόν ἐστιν ἄρα καὶ ἐκκεκλιμένου τὴν κλίσιν εἰπεῖν, τουτέστιν ἐν ποίαι γωνίαι κέκλιται τὸ ἐπίπεδον πρὸς τὸ παράλληλον τῶι ὁρίζοντι.
17. ιʹ. Βάρους δοθέντος ὑπὸ δοθείσης ἀγομένου δυνάμεως ἐν τῶι παρὰ τὸν ὁρίζοντα ἐπιπέδωι καὶ ἑτέρου ἐπιπέδου κεκλιμένου πρὸς τὸ ὑποκείμενον δοθεῖσαν γωνίαν ὑποτιθέντος, εὑρεῖν τὴν δύναμιν ὑφ' ὅσης ἀχθήσεται τὸ βάρος ἐν τῶι κεκλιμένωι ἐπιπέδωι.
Ἔστω τὸ μὲν διὰ τῆς ΜΝ εὐθείας ἐπίπεδον τὸ ὑποκείμενον, τὸ δὲ διὰ τῆς ΜΚ κεκλιμένον πρὸς αὐτὸ γωνίαν δοθεῖσαν τὴν ὑπὸ ΚΜΝ ὑποτιθέν, βάρος δέ τι τὸ Α κινείσθω ὑπὸ δυνάμεως τῆς Γ ἐπὶ τοῦ ὑποκειμένου ἐπιπέδου, καὶ νοείσθω τῶι Α ἰσοβαρὴς σφαῖρα ἡ περὶ κέντρον τὸ Ε, καὶ κείσθω ἐπὶ τοῦ διὰ τῶν Μ Κ ἐπιπέδου ψαύουσα αὐτοῦ κατὰ τὸ Λ σημεῖον, ὡς ἔστιν σφαιρικῶν γʹ θεωρήματι· ἡ ἄρα ΕΛ ἐπιζευχθεῖσα κάθετος ἔσται ἐπὶ τὸ ἐπίπεδον [καὶ τοῦτο γὰρ δέδεικται θεωρήματι δʹ σφαιρικῶν], ὥστε καὶ πρὸς τὴν ΚΜ κάθετός ἐστιν ἡ ΕΛ. ἐκβεβλήσθω τὸ διὰ τῶν ΚΜ ΕΛ ἐπίπεδον καὶ ποιείτω τομὴν ἐν τῆι σφαίραι κύκλον τὸν ΛΗΞ, καὶ ἤχθω διὰ τοῦ Ε κέντρου τῆι ΜΝ παράλληλος ἡ ΕΘ, καὶ κάθετος ἐπ' αὐτὴν ἀπὸ τοῦ Λ ἡ ΛΖ. ἐπεὶ οὖν δοθεῖσά ἐστιν ἡ ὑπὸ ΕΘΛ γωνία [ἴση γάρ 1 - 10 11 - 20 21 - 30 31 - 40 41 - 50 51 - 57 51 52 53 54 55 56 57 ἐστιν τῆι ὑπὸ ΚΜΝ δοθείσηι [ὀξείαι] γωνίαι], δοθεῖσα ἄρα καὶ ἡ ὑπὸ ΕΛΖ ἴση οὖσα τῆι ὑπὸ ΕΘΛ [ἰσογώνιον γάρ ἐστιν τὸ ΕΘΛ τῶι ΕΛΖ τριγώνωι]· δοθὲν ἄρα τὸ ΕΛΖ τρίγωνον τῶι εἴδει· λόγος ἄρα τῆς ΕΛ, τουτέστιν τῆς ΕΗ, πρὸς ΕΖ δοθείς· καὶ λοιπῆς ἄρα τῆς ΖΗ πρὸς ΕΖ λόγος ἐστὶν δοθείς. πεποιήσθω οὖν ὡς ἡ ΗΖ πρὸς ΖΕ, οὕτως τὸ μὲν Α βάρος πρὸς τὸ Β, ἡ δὲ Γ δύναμις πρὸς τὴν Δ. καὶ ἔστιν τοῦ Α δύναμις ἡ Γ· καὶ τοῦ Β ἄρα δύναμις ἐν τῶι αὐτῶι ἐπιπέδωι ἔσται ἡ Δ. καὶ ἐπεί ἐστιν ὡς ἡ ΗΖ εὐθεῖα πρὸς τὴν ΖΕ, οὕτως τὸ Α βάρος πρὸς τὸ Β, ἂν τεθῆι τὰ Α Β βάρη περὶ κέντρα τὰ Ε Η, ἰσορροπήσει ἀρτώμενα ἀπὸ τοῦ Ζ σημείου [ἢ ἐπὶ ὑποθέματος κείμενα τοῦ ΛΖ ὀρθοῦ πρὸς τὸν ὁρίζοντα]. κεῖται δὲ τὸ Α βάρος περὶ κέντρον τὸ Ε [ἀντ' αὐτοῦ γὰρ ἡ σφαῖρα]· τεθὲν ἄρα τὸ Β βάρος περὶ κέντρον τὸ Η ἰσορροπήσει τῆι σφαίραι, ὥστε μὴ καταφέρεσθαι τὴν σφαῖραν διὰ τὴν κλίσιν τοῦ ἐπιπέδου, ἀλλ' ἐφεστάναι ἀρρεπῆ, ὡς εἰ καὶ ἐπὶ τοῦ ὑποκειμένου ἑστῶσα ἐτύγχανεν. ἐκινεῖτο δὲ ἐν τῶι ὑποκειμένωι ἐπιπέδωι ὑπὸ τῆς Γ δυνάμεως· κινηθήσεται ἄρα ἐν τῶι κεκλιμένωι ἐπιπέδωι πρὸς συναμφοτέρου τῆς τε Γ δυνάμεως καὶ τῆς τοῦ Β βάρους, τουτέστιν τῆς Δ δυνάμεως. καὶ ἔστιν δοθεῖσα ἡ Δ δύναμις.
18. Ἡ μὲν οὖν γεωμετρικὴ τοῦ προβλήματος ἀνάλυσις ὑποδέδεικται, ἵνα δὲ καὶ ἐπὶ παραδείγματος ποιησώμεθα τήν τε κατασκευὴν καὶ τὴν ἀπόδειξιν, ἔστω τὸ μὲν Α βάρος ταλάντων, εἰ τύχοι, σʹ ἀγόμενον ἐν τῶι παραλλήλωι ὁρίζοντι ἐπιπέδωι ὑπὸ τῆς Γ κινούσης δυνάμεως, τουτέστιν οἱ κινοῦντες ἔστωσαν ἄνθρωποι μʹ, ἡ δὲ ὑπὸ ΚΜΝ γωνία, τουτέστιν ἡ ὑπὸ ΕΘΛ, διμοίρου ὀρθῆς· καὶ λοιπὴ ἄρα ἡ ὑπὸ ΖΛΘ τρίτου ὀρθῆς. καὶ ἔστιν ὀρθὴ ἡ ὑπὸ ΕΛΘ· διμοίρου ἄρα καὶ ἡ ὑπὸ ΕΛΖ· οἵων ἄρα αἱ δʹ ὀρθαὶ τξʹ τοιούτων ξʹ ἡ ὑπὸ ΕΛΖ, καὶ τοῦ περιγραφομένου ἄρα περὶ τὸ ΕΖΛ τρίγωνον ὀρθογώνιον κύκλου ἡ μὲν ἐπὶ τῆς ΕΖ περιφέρεια τοιούτων ἔσται ρκʹ οἵων ὁ κύκλος τξʹ, αὐτὴ δὲ ἡ ΕΖ τοιούτων ρδʹ ἔγγιστα οἵων ἡ ΕΛ τοῦ κύκλου διάμετρος ρκʹ· ταῦτα γὰρ δῆλα ἐκ τοῦ κανόνος τῶν ἐγκυκλίων εὐθειῶν τοῦ κατὰ Πτολεμαῖον [ὄντος] κειμένου ἐν τῶι αʹ τῶν μαθηματικῶν. λόγος ἄρα τῆς ΕΛ, τουτέστιν τῆς ΕΗ, πρὸς ΕΖ, ὃν ρκʹ πρὸς ρδʹ· καὶ λοιπῆς ἄρα τῆς ΗΖ πρὸς ΖΕ λόγος ὃν ιςʹ πρὸς ρδʹ. τούτωι δὲ ὁ αὐτός ἐστιν ὁ τοῦ Α βάρους πρὸς τὸ Β, καὶ τῆς Γ δυνάμεως πρὸς τὴν Δ, καὶ ἔστιν τὸ μὲν Α βάρος ταλάντων σʹ, ἡ δὲ κινοῦσα δύναμις ἀνδρῶν μʹ· ἔσται ἄρα καὶ τὸ μὲν Β βάρος ταλάντων ͵ατʹ, ἡ δὲ Δ δύναμις ἀνθρώπων σξʹ (ὡς γὰρ ιςʹ πρὸς ρδʹ, οὕτως σʹ πρὸς ͵ατʹ καὶ μʹ πρὸς σξʹ)· τοῦ ἄρα Α βάρους ταλάντων σʹ κινουμένου ἐν παραλλήλωι τῶι ὁρίζοντι ἐπιπέδωι ὑπὸ τῶν μʹ ἀνδρῶν, τὸ αὐτὸ βάρος κινηθήσεται ὑπὸ συναμφοτέρων τῶν προειρημένων ἀνθρώπων, τουτέστιν ὑπὸ τʹ ὅλων, ἐν ἐπιπέδωι κεκλιμένωι πρὸς τὸν ὁρίζοντα, τῆς ὑπὸ ΚΜΝ γωνίας διμοίρου ὀρθῆς ὑποκειμένης.
19. ιαʹ. Τῆς αὐτῆς δέ ἐστιν θεωρίας τὸ δοθὲν βάρος τῆι δοθείσηι δυνάμει κινῆσαι· τοῦτο γὰρ Ἀρχιμήδους μὲν εὕρημα [λέγεται] μηχανικόν, ἐφ' ὧι λέγεται εἰρηκέναι· δός μοί (φησι) ποῦ στῶ καὶ κινῶ τὴν γῆν. Ἥρων δὲ ὁ Ἀλεξανδρεὺς πάνυ σαφῶς αὐτοῦ τὴν κατασκευὴν ἐξέθετο ἐν τῶι καλουμένωι βαρουλκῶι, λῆμμα λαβὼν ὅπερ ἐν τοῖς μηχανικοῖς ἀπέδειξεν, ἔνθα καὶ περὶ τῶν εʹ δυνάμεων διαλαμβάνει, τουτέστιν τοῦ τε σφηνὸς καὶ μοχλοῦ καὶ κοχλίου καὶ πολυσπάστου καὶ ἄξονος ἐν τῶι περιτροχίωι, δι' ὧν τὸ δοθὲν βάρος τῆι δοθείσηι δυνάμει κινεῖται [καθ' ἑκάστην δύναμιν]. ἐν δὲ τῶι βαρουλκῶι διὰ τυμπάνων ὀδοντωτῶν παραθέσεως ἐκίνει τὸ δοθὲν βάρος τῆι δοθείσηι δυνάμει, τῆς διαμέτρου τοῦ τυμπάνου πρὸς τὴν διάμετρον τοῦ ἄξονος λόγον ἐχούσης ὃν εʹ πρὸς αʹ, τοῦ κινουμένου βάρους ὑποκειμένου ταλάντων χιλίων, τῆς δὲ κινούσης δυνάμεως ὑποκειμένης ταλάντων εʹ.
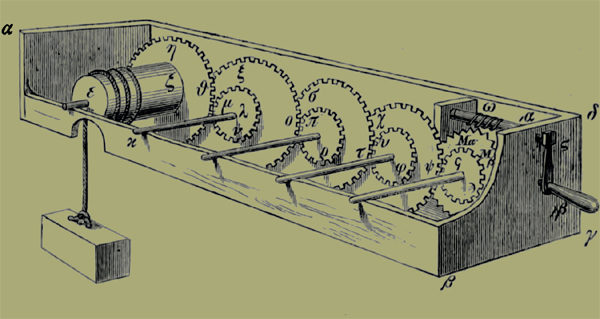
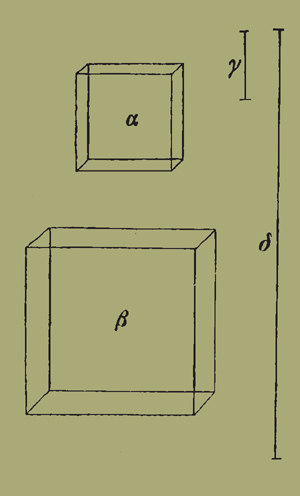
20. Ἔστω δὴ ἡμᾶς ἐπὶ διπλασίου λόγου τὸ αὐτὸ δεικνύναι, καὶ ταλάντων ρξʹ ὄντος τοῦ κινουμένου βάρους ἀντὶ χιλίων, καὶ τῆς κινούσης αὐτὸ δυνάμεως ὑποκειμένης ταλάντων δʹ ἀντὶ εʹ, τουτέστιν ὁ κινῶν ἄνθρωπος δυνάσθω καθ' αὑτὸν ἄνευ μηχανῆς ἕλκειν τάλαντα δʹ, καὶ ἔστω τὸ εἰρημένον ὑπ' αὐτοῦ γλωσσόκομον τὸ ΑΒΓΔ, καὶ ἐν αὐτῶι εἰς τοὺς μακροὺς καὶ παραλλήλους τοίχους ἔστω ἄξων διακείμενος εὐλύτως στρεφόμενος ὁ ΕΖ, τούτωι δὲ συμφυὲς ἔστω τύμπανον ὠδοντωμένον [ἀκτῖσιν ὀδοντωτοῖς] τὸ ΗΘ, ἔχον τὴν διάμετρον διπλασίαν τῆς διαμέτρου [τῆς ΕΖ διαγωνίου] τοῦ ἄξονος τῆς κατὰ κότραφον [γίνεται γὰρ τετράγωνος μὲν περὶ μέσον ἐπὶ τοσοῦτον μῆκος, ὅσον ἐστὶν τὸ πάχος τοῦ τυμπάνου εἰς ὃ ἐναρμόζεται ἀσφαλῶς, στρογγύλος δέ πως ἢ λελοιφωμένος ἐκ τῶν ἐφ' ἑκάτερα τοῦ τυμπάνου μερῶν]. ἐὰν ἄρα τὰ ἐκ τοῦ βάρους τοῦ ἑλκομένου δεδεμένα σχοινία [καλούμενα δὲ ὅπλα] διά τινος ὀπῆς [μᾶλλον δὲ ἀνατομῆς πλατείας] οὔσης ἐν τῶι ΑΒ τοίχωι ἐπειληθῆι περὶ τὸν ΕΖ ἄξονα [ἐφ' ἑκάτερα τοῦ ΗΘ τυμπάνου] καὶ στραφῆι τὸ ΗΘ τύμπανον, τοῦτο ἐπιστρέψει καὶ τὸν συμφυῆ ἄξονα κινού μενον περὶ τὰ ἄκρα ἐν δακτύλοις χαλκοῖς καὶ πυξίσιν ὁμοίως χαλκαῖς [κινουμέναις], κειμέναις δ' ἐν τοῖς εἰρημένοις ΑΒ ΓΔ τοίχοις. ἐπειλούμενα δὲ τὰ ἐκ τοῦ βάρους [ὃ καλεῖται φορτίον] ὅπλα κινήσει τὸ βάρος. ἵνα δὲ κινηθῆι τὸ ΗΘ τύμπανον, δεήσει δύναμιν παρασχεῖν ταλάντων πλεῖον πʹ διὰ τὸ τὴν διάμετρον τοῦ τυμπάνου τῆς διαμέτρου τοῦ ἄξονος εἶναι διπλασίαν· τοῦτο γὰρ πρόβλημά ἐστιν ὑπὸ Ἥρωνος δεικνύμενον ἐν τοῖς μηχανικοῖς. [καὶ ἄλλα πλεῖστα προβλήματα τῶν χρησιμωτάτων καὶ βιωφελῶν γέγραπται].
21. Ἐπεὶ οὖν οὐκ ἔχομεν τὴν δοθεῖσαν δύναμιν ταλάντων πʹ, ἀλλὰ ταλάντων δʹ, γεγονέτω ἕτερος ἄξων παρακείμενος παράλληλος τῶι ΕΖ ὁ ΚΛ, ἔχων συμφυὲς τύμπανον ὠδοντωμένον τὸ ΜΝ, ὥστε τοὺς ὀδόντας αὐτοῦ ἐναρμόζειν τοῖς ὀδοῦσι τοῦ ΗΘ τυμπάνου· τοῦτο δὲ γίνεται, ἐὰν ἦι ὡς ἡ διάμετρος τοῦ ΗΘ τυμπάνου πρὸς τὴν διάμετρον τοῦ ΜΝ, οὕτως τὸ πλῆθος τῶν ὀδόντων τοῦ ΗΘ πρὸς τὸ πλῆθος τῶν ὀδόντων τοῦ ΜΝ (πῶς δὲ τοῦτο γίνεται διὰ τῶν ἑξῆς δῆλον ἔσται)· δοθὲν μὲν ἄρα ἐστὶν καὶ τὸ ΜΝ τύμπανον. τῶι δ' αὐτῶι ἄξονι τῶι ΚΛ συμφυὲς ἔστω τύμπανον τὸ ΞΟ, ἔχον τὴν διάμετρον διπλασίαν τῆς τοῦ ΜΝ τυμπάνου διαμέτρου. διὰ δὴ τοῦτο δεήσει τὸν βουλόμενον κινεῖν διὰ τοῦ ΞΟ τυμπάνου τὸ βάρος ἔχειν δύναμιν ταλάντων μʹ, ἐπειδήπερ τὰ πʹ τάλαντα διπλάσιά ἐστιν τῶν μʹ ταλάντων.
22. Πάλιν δὲ παρακείσθω τῶι ΞΟ τυμπάνωι [ὀδοντωθέντι] ἕτερον τύμπανον ὠδοντωμένον τὸ ΠΡ συμφυὲς ἑτέρωι ἄξονι, τῶι δ' αὐτῶι ἄξονι ἕτερον συμφυὲς τύμπανον τὸ ΣΤ, ἔχον μὲν ὁμοίως διπλασίαν τὴν διάμετρον τῆς τοῦ ΠΡ τυμπάνου διαμέτρου, τοὺς δὲ ὀδόντας μὴ συμπλεκομένους τοῖς ὀδοῦσι τοῦ ΜΝ τυμπάνου· ἡ ἄρα διὰ τοῦ ΣΤ τυμπάνου κινοῦσα τὸ βάρος δύναμις ἔσται ταλάντων κʹ. ἦν δὲ ἡ δοθεῖσα δύναμις ταλάντων δʹ· δεήσει οὖν πάλιν ἕτερον μὲν τύμπανον ὠδοντωμένον τὸ ΥΦ παρακεῖσθαι τῶι ΣΤ [ὀδοντωθέντι], τῶι δὲ ἄξονι τοῦ ΥΦ τυμπάνου συμφυὲς γενέσθαι τὸ ΧΨ ὠδοντωμένον, οὗ ἡ διάμετρος πρὸς τὴν τοῦ ΥΦ τυμπάνου διάμετρον λόγον ἐχέτω ὃν τὰ βʹ πρὸς αʹ· ἡ ἄρα κινοῦσα τὸ βάρος δύναμις διὰ τοῦ ΧΨ τυμπάνου ἔσται ταλάντων ιʹ. πάλιν δὴ παρακείσθω μὲν τῶι ΧΨ τυμπάνωι ἕτερον τύμπανον ὠδοντωμένον τὸ ϞϠ, τῶι δὲ ἄξονι αὐτοῦ τύμπανον ἔστω συμφυὲς ΜαΜβ ὠδοντωμένον ὀδοῦσιν λοξοῖς, οὗ ἡ διάμετρος πρὸς τὴν τοῦ ϞϠ διάμετρον λόγον ἐχέτω ὃν ἔχει τὰ ιʹ τάλαντα πρὸς τὰ τῆς δοθείσης δυνάμεως τάλαντα δʹ.
23. Καὶ τούτων κατασκευασθέντων ἐὰν ἐπινοήσωμεν τὸ ΑΒΓΔ γλωσσόκομον μετέωρον κείμενον ἀμεταστάτως, καὶ ἐκ μὲν τοῦ ΕΖ ἄξονος βάρος ἐξάψωμεν, ἐκ δὲ τοῦ ΜαΜβ τυμπάνου τὴν ἕλκουσαν δύναμιν τὰ δʹ τάλαντα, οὐδοπότερον αὐτῶν κατενεχθήσεται, εὐλύτως στρεφομένων τῶν ἀξόνων καὶ τῆς τῶν τυμπάνων παραθέσεως ἀκριβῶς ἁρμοζούσης, ἀλλ' ὥσπερ ἐπὶ ζυγοῦ τινος ἰσορροπήσει ἡ δύναμις τῶν δʹ ταλάντων τῶι βάρει τῶν ρξʹ ταλάντων· ἐὰν ἄρα ἑνὶ αὐτῶν προσθῶμεν ὀλίγον τι βάρος, καταρρέψει καὶ ἐνεχθήσεται ἐφ' ὁπότερον μέρος ἡ πρόσθεσις γεγένηται· εἰ γὰρ λόγου χάριν τῆι τῶν δʹ ταλάντων δυνάμει μναιαῖον προστεθῆι βάρος, κατακρατῆσαν ἐπισπάσεται τὸ βάρος τῶν ρξʹ ταλάντων. 24. ἀντὶ δὲ τῆς προσθέσεως παρακείσθω κοχλίας τῶι ΜαΜβ τυμπάνωι ὁ ΩΑʹ ἔχων τὴν ἕλικα ἁρμόζουσαν τοῖς λοξοῖς ὀδοῦσι τοῦ τυμπάνου τοῦ ΜαΜβ. τοῦτο δὲ ὡς δεῖ ποιεῖν, ἐν τοῖς αὐτοῖς μηχανικοῖς Ἥρωνος γέγραπται, καὶ ἡμεῖς δὲ τοῦτο σαφέστερον ἑξῆς γράψομεν. στρεφέσθω δὲ ὁ κοχλίας εὐλύτως περὶ τόρμους ἐνόντας ἐν τρήμασι στρογγύλοις, ὧν ὁ ἕτερος ὑπερεχέτω εἰς τὸ ἐκτὸς μέρος τοῦ γλωσσοκόμου κατὰ τὸν ΓΔ τοῖχον, καὶ ἡ ὑπεροχὴ τετραγωνισθεῖσα λαβέτω χειρολάβην τὴν ς͵Β, δι' ἧς ἐπιλαβόμενοι καὶ ἐπιστρέφοντες τὸν κοχλίαν ἐπιστρέψομεν καὶ τὸ ΜαΜβ τύμπανον, ὥστε καὶ τὸ ϞϠ συμφυὲς αὐτῶι. διὰ δὲ τοῦτο καὶ τὸ παρακείμενον αὐτῶι τὸ ΧΨ στραφήσεται, καὶ τὸ συμφυὲς αὐτῶι τὸ ΥΦ, καὶ τὸ παρακείμενον αὐτῶι τὸ ΣΤ, καὶ τὸ τούτωι συμφυὲς τὸ ΠΡ, καὶ τὸ τούτωι παρακείμενον τὸ ΞΟ, καὶ τὸ τούτωι συμφυὲς τὸ ΜΝ, καὶ τὸ τούτωι παρακείμενον τὸ ΗΘ, ὥστε καὶ ὁ τούτωι συμφυὴς ἄξων ὁ ΕΖ, περὶ ὃν ἐπειλοῦντες τὰ ἐκ τοῦ φορτίου ὅπλα κινήσομεν τὸ βάρος. ὅτι γὰρ κινήσεται δῆλον ἐκ τοῦ προστεθεῖσθαι ἑτέραν δύναμιν τὴν τῆς χειρολάβης, ἥτις περιγράφει κύκλον τῆς τοῦ κοχλίου περιμέτρου μείζονα· ἀπεδείχθη γὰρ ἐν τῶι περὶ ζυγῶν Ἀρχιμήδους καὶ τοῖς Φίλωνος καὶ Ἥρωνος μηχανικοῖς, ὅτι οἱ μείζονες κύκλοι κατακρατοῦσιν τῶν ἐλασσόνων κύκλων, ὅταν περὶ τὸ αὐτὸ κέντρον ἡ κύλισις αὐτῶν γίνηται.
25. ιβʹ. Τὰ μὲν οὖν μάλιστα συνέχοντα τὴν μηχανικὴν θεωρίαν ταῦτ' ἂν εἴη. τῆς δὲ ὀργανικῆς πολλὰ μὲν εἴδη καὶ μέρη· τὰ μὲν γὰρ ὑπὸ τῆς μηχανικῆς καὶ γνωμονικῆς καὶ τῆς περὶ ὑδρείων πραγματείας λόγωι θεωρούμενα δι' αὐτῶν τῶν ὀργάνων ὑπὸ ταύτης κατασκευαζόμενα δείκνυται, πολλὰ δὲ καὶ χωρὶς τῶν μηχανικῶν ἔξωθεν ὑπ' αὐτῆς ἐπιτελεῖται, καί τινα ταῖς γεωμετρικαῖς ἐφόδοις δυσχείριστα μεταλαβοῦσα τοῖς ὀργάνοις εἰς ῥαιδιεστέραν ἤγαγε κατασκευήν. αὐτίκα γοῦν τὸ καλούμενον Δηλιακὸν πρόβλημα τῆι φύσει στερεὸν ὑπάρχον οὐχ οἷόν τ' ἦν κατασκευάσαι τῶι γεωμετρικῶι λόγωι κατακολουθοῦντας, ἐπεὶ μηδὲ τὰς τοῦ κώνου τομὰς ῥάιδιον ἐν ἐπιπέδωι γράφειν ἦν, τοῖς δ' ὀργάνοις μεταληφθὲν εἰς χειρουργίαν καὶ κατασκευὴν ἐπιτήδειον [μᾶλλον τῆς ὑπὸ τῶν ἄλλων ἐκτεθειμένης οὕτως] ἂν ἀναχθείη [τὸ προκείμενον], λέγω δὲ τὸ κύβον κύβου διπλάσιον εὑρεῖν. οὐ μόνον δὲ διπλάσιος εὑρίσκεται διὰ τοῦ ὑποκειμένου ὀργάνου, ἀλλὰ καὶ καθόλου λόγον ἔχων τὸν ἐπιταχθέντα.
26. Κατεσκευάσθω γὰρ ἡμικύκλιον τὸ ΑΒΓ, καὶ ἀπὸ τοῦ Δ κέντρου πρὸς ὀρθὰς ἀνήχθω ἡ ΔΒ, καὶ κινείσθω κανόνιόν τι περὶ τὸ Α σημεῖον οὕτως ὥστε τὸ μὲν ἓν πέρας αὐτοῦ περικεῖσθαι τυλίωι τινὶ κατὰ τὸ Α σημεῖον ἑστῶτι, τὸ δὲ λοιπὸν μέρος ὡς περὶ κέντρον τὸ τυλάριον κινεῖσθαι μεταξὺ τῶν Β Γ. τούτων δὲ κατεσκευασμένων ἐπιτετάχθω δύο κύβους εὑρεῖν λόγον ἔχοντας πρὸς ἀλλήλους δοθέντα, καὶ τῶι λόγωι ὁ αὐτὸς πεποιήσθω ὁ τῆς ΒΔ πρὸς ΔΕ, καὶ ἐπιζευχθεῖσα ἡ ΓΕ ἐκβεβλήσθω ἐπὶ τὸ Ζ. παραγέσθω δὴ τὸ κανόνιον μεταξὺ τῶν Β Γ, ἕως οὗ τὸ ἀπολαμβανόμενον αὐτοῦ μέρος μεταξὺ τῶν ΖΕ ΕΒ εὐθειῶν ἴσον γένηται τῶι μεταξὺ τῆς ΒΕ εὐθείας καὶ τῆς ΒΚΓ περιφερείας· τοῦτο γὰρ πειράζοντες αἰεὶ καὶ μετάγοντες τὸ κανόνιον ῥαιδίως ποιήσομεν. γεγονέτω δή, καὶ ἐχέτω θέσιν τὴν ΑΗΘΚ, ὥστε ἴσας εἶναι τὰς ΗΘ ΘΚ· λέγω ὅτι ὁ ἀπὸ τῆς ΒΔ κύβος πρὸς τὸν ἀπὸ τῆς ΔΘ κύβον λόγον ἔχει τὸν ἐπιταχθέντα, τουτέστιν τὸν τῆς ΒΔ πρὸς ΔΕ.
Νοείσθω γὰρ ὁ κύκλος προσαναπεπληρωμένος, καὶ ἐπιζευχθεῖσα ἡ ΚΔ ἐκβεβλήσθω ἐπὶ τὸ Λ, καὶ ἐπεζεύχθω ἡ ΛΗ· παράλληλος ἄρα ἐστὶν τῆι ΒΔ διὰ τὸ ἴσην εἶναι τὴν μὲν ΚΘ τῆι ΘΗ, τὴν δὲ ΚΔ τῆι ΔΛ. ἐπεζεύχθω δὴ καὶ ἥ τε ΑΛ καὶ ἡ ΛΓ. ἐπεὶ οὖν ὀρθή ἐστιν ἡ ὑπὸ ΗΑΛ ἐν ἡμικυκλίωι καὶ κάθετος ἡ ΑΜ, ἔστιν ἄρα ὡς τὸ ἀπὸ ΛΜ πρὸς τὸ ἀπὸ ΜΑ, τουτέστιν ὡς ἡ ΓΜ πρὸς ΜΑ, οὕτως τὸ ἀπὸ ΑΜ πρὸς τὸ ἀπὸ ΜΗ. κοινὸς προσκείσθω λόγος ὁ τῆς ΑΜ πρὸς ΜΗ· ὁ ἄρα συγκείμενος ἔκ τε τοῦ τῆς ΓΜ πρὸς ΜΑ καὶ τοῦ τῆς ΑΜ πρὸς ΜΗ, τουτέστιν ὁ τῆς ΓΜ πρὸς ΜΗ, λόγος ὁ αὐτός ἐστιν τῶι συγκειμένωι ἔκ τε τοῦ τοῦ ἀπὸ τῆς ΑΜ πρὸς τὸ ἀπὸ τῆς ΜΗ καὶ ἐκ τοῦ τῆς ΑΜ πρὸς ΜΗ. ὁ δὲ συγκείμενος ἔκ τε τοῦ τοῦ ἀπὸ τῆς ΑΜ πρὸς τὸ ἀπὸ τῆς ΜΗ καὶ τοῦ τῆς ΑΜ πρὸς ΜΗ ὁ αὐτός ἐστιν τῶι λόγωι ὃν ἔχει ὁ ἀπὸ τῆς ΑΜ κύβος πρὸς τὸν ἀπὸ τῆς ΜΗ κύβον· καὶ ὁ τῆς ΓΜ ἄρα πρὸς τὴν ΜΗ λόγος ὁ αὐτός ἐστιν τῶι λόγωι τοῦ ἀπὸ τῆς ΑΜ κύβου πρὸς τὸν ἀπὸ τῆς ΜΗ κύβον. ἀλλ' ὡς μὲν ἡ ΓΜ πρὸς ΜΗ, οὕτως ἡ ΓΔ πρὸς ΔΕ, τουτέστιν ἡ ΒΔ πρὸς ΔΕ, ὡς δὲ ἡ ΑΜ πρὸς ΜΗ, οὕτως ἡ ΑΔ πρὸς ΔΘ, τουτέστιν ἡ ΔΒ πρὸς ΔΘ· καὶ ὡς ἄρα ἡ ΒΔ πρὸς ΔΕ, τουτέστιν ὡς ὁ δοθεὶς λόγος, οὕτως ὁ ἀπὸ τῆς ΒΔ κύβος πρὸς τὸν ἀπὸ τῆς ΔΘ κύβον.
Πρόβλημα ὀργανικὸν ἐπὶ κυλίνδρου.
27. ιγʹ. Τὰ δ' ὀργανικὰ ἐν τοῖς μηχανικοῖς λεγόμενα προ βλήματά [ἐστιν ὅτι] γίνεται τῆς γεωμετρικῆς ἐξουσίας ἀφαιρούμενα, οἷά ἐστιν καὶ τὰ ἑνὶ διαστήματι γραφόμενα καὶ τὸ ἐπὶ τοῦ τὰς βάσεις ἀμφοτέρας λελωβημένου κυλίνδρου προτεινόμενον ὑπὸ τῶν ἀρχιτεκτόνων. ἀξιοῦσι γὰρ μέρους ἐπιφανείας ὀρθοῦ κυλίνδρου δοθέντος, οὗ μηδὲν μέρος ὑγιὲς φυλάσσεται τῶν ἐν ταῖς βάσεσι περιφερειῶν, εὑρεῖν τὸ πάχος τοῦ κυλίνδρου, τουτέστιν τοῦ κύκλου τὴν διάμετρον ἀφ' οὗ τὴν γένεσιν ἔσχεν ὁ κύλινδρος. εὑρίσκεται δὲ μεθοδευθὲν οὕτως.
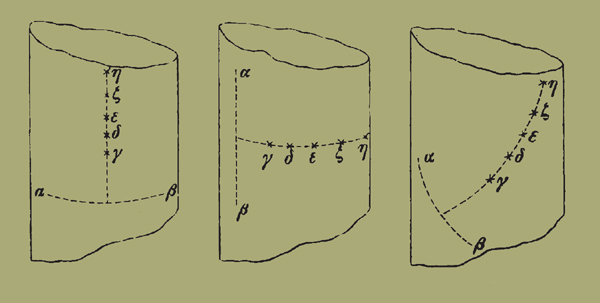
28. Εἰλήφθω ἐπὶ τῆς δοθείσης ἐπιφανείας δύο σημεῖα τὰ Α Β, καὶ κέντροις αὐτοῖς ἑνὶ διαστήματι σεσημειώσθω ἐπὶ τῆς ἐπιφανείας πρῶτον τὸ Γ, καὶ πάλιν κέντροις αὐτοῖς τοῖς Α Β διαστήματι τοῦ προτέρου μείζονι σεσημειώσθω τὸ Δ, καὶ ἄλλωι διαστήματι τὸ Ε, καὶ ἄλλωι τὸ Ζ, καὶ ἄλλωι τὸ Η. ἔσται δὴ τὰ εʹ σημεῖα τὰ Γ Δ Ε Ζ Η ἐν ἑνὶ ἐπιπέδωι διὰ τὸ καὶ τὴν ἐπιζευγνύουσαν ἕκαστον αὐτῶν ὡς κορυφὴν ἰσοσκελοῦς τριγώνου τῆι διχοτομίαι τῆς ἐπιζευγνούσης εὐθείας τὰ Α Β ὡς βάσεως κοινῆς τῶν τριγώνων ὀρθὴν εἶναι πρὸς τὴν ΑΒ [καὶ ἐν ἑνὶ γίνεσθαι ἐπιπέδωι τὰς εʹ εὐθείας, καὶ δῆλον ὅτι τὰ Γ Δ Ε Ζ Η σημεῖα]. ταῦτα δὲ εἰς ἐπίπεδον ἐκθησόμεθα οὕτως· ἐκ τριῶν μὲν εὐθειῶν τῶν ἐπιζευγνυουσῶν τὰ Γ Δ Ε τρίγωνον ἐν τῶι ἐπιπέδωι συνεστάτω τὸ ΘΚΛ, ἐκ τριῶν δὲ τῶν ἐπιζευγνυουσῶν τὰ Δ Ε Ζ τὸ ΚΛΜ, ἐκ τριῶν δὲ τῶν ἐπιζευγνυουσῶν τὰ Ε Ζ Η σημεῖα τρίγωνον συνεστάτω τὸ ΛΜΝ· ἔσται ἄρα ἐκκείμενα τὰ ΘΚΛ ΚΛΜ ΛΜΝ τρίγωνα ἀντὶ τῶν ΓΔΕ ΔΕΖ ΕΖΗ τριγώνων. ἂν δὴ περὶ τὰ Θ Κ Λ Μ Ν σημεῖα γράψωμεν ἔλλειψιν, ὁ ἐλάσσων αὐτῆς ἄξων διάμετρος ἔσται τοῦ κύκλου τοῦ τὸν κύλινδρον ἀπεργασαμένου.
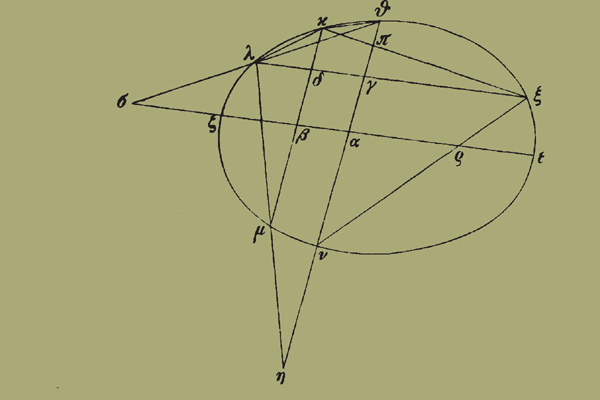
29. ιδʹ. Ζητουμένου δὴ περὶ πέντε τὰ δοθέντα σημεῖα ἐν ἑνὶ ἐπιπέδωι κείμενα τὰ Θ Κ Λ Μ Ν ἔλλειψιν γράψαι, περιγεγράφθω, καὶ ἐπιζευχθεῖσαι αἱ ΘΝ ΜΚ πρότερον ἔστωσαν παράλληλοι, καὶ δίχα τετμήσθω ἑκατέρα αὐτῶν τοῖς Α Β, καὶ ἐπιζευχθεῖσα ἡ ΑΒ ἐκβεβλήσθω ἐπὶ τὰ Ε Ζ τῆς ἐλλείψεως σημεῖα· ἡ ΕΖ ἄρα διάμετρός ἐστιν τῆς ἐλλείψεως διὰ τὸν ιʹ ὅρον τῶν κωνικῶν, θέσει δεδομένη· δοθὲν γὰρ καὶ ἑκάτερον τῶν Α Β σημείων τῆι θέσει. ἤχθω δὴ διὰ τοῦ Λ τῆι ΕΖ παράλληλος ἡ ΛΞ, καὶ ἐπιζευχθεῖσαι αἱ ΞΚ ΛΜ συμπιπτέτωσαν τῆι ΘΝ ἐκβληθείσηι κατὰ τὰ Π Η· δοθέντα ἄρα τὰ Γ Η (δοθὲν γὰρ ἕκαστον τῶν Λ Μ Θ Ν). καὶ ἐπεὶ ὡς τὸ ὑπὸ ΞΔΛ πρὸς τὸ ὑπὸ τῶν ΜΔΚ, οὕτως τὸ ὑπὸ ΞΓΛ πρὸς ἑκάτερον τῶν ὑπὸ ΗΓΠ ΝΓΘ, ἔσται ἄρα ἴσον τὸ ὑπὸ ΗΓΠ τῶι ὑπὸ ΝΓΘ. καὶ ἔστιν δοθὲν τὸ ὑπὸ ΝΓΘ (δοθεῖσα γὰρ ἑκατέρα)· δοθὲν ἄρα τὸ Π. ἀλλὰ καὶ τὸ Κ· θέσει ἄρα ἡ ΚΠΞ. ἀλλὰ καὶ ἡ ΛΓΞ· δοθὲν ἄρα τὸ Ξ. καὶ ἔστιν ἐπὶ τῆς ἐλλείψεως. ἐπιζευχθεῖσαι δὴ αἱ ΝΞ ΛΘ συμπιπτέτωσαν τῆι ΕΖ διαμέτρωι ἐκβληθείσηι κατὰ τὰ Ρ Σ· ἔσται δὴ πάλιν ὡς τὸ ὑπὸ ΝΓΘ πρὸς τὸ ὑπὸ ΞΓΛ, οὕτως τὸ ὑπὸ ΝΑΘ πρὸς ἑκάτερον τῶν ὑπὸ ΡΑΣ ΕΑΖ, καὶ διὰ τοῦτο ἴσον τὸ ὑπὸ ΡΑΣ τῶι ὑπὸ ΕΑΖ. καὶ ἔστιν δοθὲν τὸ ὑπὸ ΡΑΣ (δοθεῖσαι γάρ εἰσιν αἱ ΡΑ ΑΣ)·
δοθὲν ἄρα καὶ τὸ ὑπὸ ΕΑ ΑΖ. τῶι δ' ὁμοίωι τρόπωι δειχθήσεται καὶ τὸ ὑπὸ ΕΒΖ δοθέν. καὶ δοθέντα τὰ Α Β· δοθέντα ἄρα καὶ τὰ Ε Ζ, ὡς ἑξῆς δειχθήσεται· ὥστε ἡ ΕΖ διάμετρος δέδοται τῶι μεγέθει. δῆλον δ' ὅτι καὶ ἡ συζυγὴς αὐτῆι· δέδοται γὰρ ὁ τῆς ΕΖ πλαγίας πρὸς τὴν ὀρθίαν αὐτῆς λόγος ὁ αὐτὸς ὢν τῶι τοῦ ὑπὸ ΕΑΖ πρὸς τὸ ἀπὸ ΑΝ.
30. ιεʹ. Τὸ ὑπερτεθέν. ἔστω δοθὲν ἑκάτερον τῶν ὑπὸ ΑΓΒ ΑΔΒ, καὶ δοθέντα τὰ Γ Δ· ὅτι τὰ Α Β δοθέντα ἐστίν.
Ἔστω γὰρ τῶι μὲν ὑπὸ ΑΓΒ ἴσον τὸ ὑπὸ ΔΓΕ, τῶι δὲ ὑπὸ ΑΔΒ ἴσον τὸ ὑπὸ ΓΔΖ· ἔσται ἄρα ὡς ἡ ΓΕ πρὸς τὴν ΕΑ, οὕτως ἡ ΑΖ πρὸς ΖΔ (διὰ γὰρ τὴν κατασκευὴν ἑκάτερος λόγος ὁ αὐτός ἐστιν τῶι τῆς ΓΒ πρὸς ΒΔ)· ἴσον ἄρα τὸ ὑπὸ ΕΓ ΖΔ τῶι ὑπὸ ΕΑΖ, ὥστε καὶ τὸ Α σημεῖον δοθέν. ὁμοίως καὶ τὸ Β.
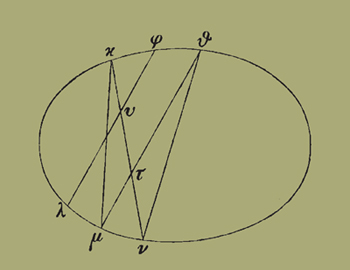
31. ιςʹ. Μὴ ἔστωσαν δὴ αἱ τὰ Ν Θ Μ Κ δεδομένα ἐπὶ τῆς ἐλλείψεως σημεῖα ἐπιζευγνύουσαι παράλληλοι, καὶ ἐπιζευχθεῖσαι αἱ ΝΚ ΜΘ τεμνέτωσαν ἀλλήλας κατὰ τὸ Τ, καὶ διὰ τοῦ Λ παράλληλος ἤχθω τῆι ΜΘ ἡ ΛΥΦ· ἔσται δὴ λόγος τοῦ ὑπὸ ΝΥΚ πρὸς τὸ ὑπὸ ΛΥΦ δοθεὶς (ὁ αὐτὸς γὰρ τῶι τοῦ ὑπὸ ΝΤΚ πρὸς τὸ ὑπὸ ΜΤΘ). καὶ δοθὲν τὸ ὑπὸ ΝΥΚ· δοθὲν ἄρα καὶ τὸ ὑπὸ ΛΥΦ· καὶ δοθέντα τὰ ΛΥ· δοθὲν ἄρα τὸ Φ· ἀπῆκται οὖν εἰς τὸ προγεγραμμένον, περὶ πέντε σημεῖα τὰ Ν Μ Λ Φ Θ γράψαι ἔλλειψιν τὴν ΝΜΛΦΘ παραλλήλων ὑποκειμένων τῶν ΜΘ ΦΛ.
32. ιζʹ. Ῥάιδιον δὲ συζυγῶν διαμέτρων ἐλλείψεως πορισθεισῶν ὡντινωνοῦν τοὺς ἄξονας αὐτῆς ὀργανικῶς εὑρεῖν. μεθοδεύεται δὲ τὸν τρόπον τοῦτον.
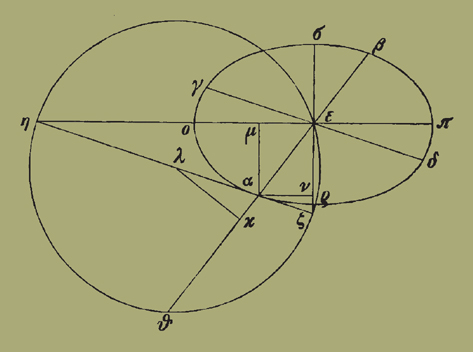
Ἐκκείσθωσαν αἱ προευρεθεῖσαι τῆς ἐλλείψεως διάμετροι συζυγεῖς αἱ ΑΒ ΓΔ δίχα τέμνουσαι ἀλλήλας κατὰ τὸ Ε, καὶ διὰ μὲν τοῦ Α τῆι ΓΔ παράλληλος ἤχθω ἡ ΖΗ, τῶι δὲ ἀπὸ ΔΕ ἴσον κείσθω τὸ ὑπὸ ΕΑΘ, καὶ ἡ ΕΘ δίχα τετμήσθω κατὰ τὸ Κ· ἔσται δὴ τὸ Κ μεταξὺ τῶν Α Θ [μείζων γάρ ἐστιν ἡ ΔΕ τῆς ΕΑ], καὶ τῆι ΕΘ πρὸς ὀρθὰς ἀπὸ τοῦ Κ ἤχθω ἡ ΚΛ τέμνουσα τὴν ΖΗ κατὰ τὸ Λ, καὶ περὶ κέντρον τὸ Λ διὰ τοῦ Ε γραφομένη κύκλου περιφέρεια τεμνέτω τὴν ΗΖ κατὰ τὰ Ζ Η, καὶ ἐπεζεύχθωσαν αἱ ΕΗ ΕΖ, καὶ κάθετοι ἤχθωσαν ἐπ' αὐτὰς αἱ ΑΜ ΑΝ, καὶ τῶι μὲν ὑπὸ ΗΕΜ ἴσον κείσθω ἑκάτερον τῶν ἀπὸ ΕΟ ΕΠ, τῶι δὲ ὑπὸ ΖΕΝ ἑκάτερον τῶν ἀπὸ ΕΡ ΕΣ· ἔσονται οὖν εὑρημένοι τῆς ἐλλείψεως ἄξονες οἱ ΟΠ ΡΣ, ὧν ὁ ἐλάχιστος ἴσος ἔσται τῶι τοῦ κυλίνδρου πάχει, καθὼς ἐν ἀρχῆι προείρηται.
33. ιηʹ. Σφαίρας μετεώρου δοθεῖσαν θέσιν ἐχούσης πρὸς τὸ ὑποκείμενον, εὑρεῖν τό τε σημεῖον ἐφ' ὃ πίπτει καθετικῶς ἐνεχθεῖσα [καὶ καθ' ὃ πίπτει σημεῖον] καὶ τὴν ἐλαχίστην ἀποτεμνομένην ἀπὸ τῆς καθέτου μεταξὺ τῶν δύο σημείων τοῦ τε κατὰ τὴν ἐπιφάνειαν τῆς σφαίρας καὶ τοῦ κατὰ τὸ ἐπίπεδον. προγράφεται δὲ τὸ κύκλου δοθέντος μετεώρου μὴ ἐν ὀρθῶι ἐπιπέδωι πρὸς τὸ ὑποκείμενον εὑρεῖν τήν τε κοινὴν τομὴν τῶν ἐπιπέδων ἀμφοτέρων καὶ τὴν κλίσιν.
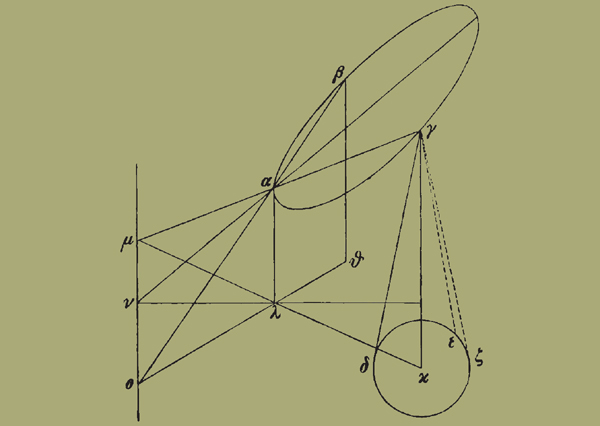
34. Ἔστω μετέωρος κύκλος, καὶ εἰλήφθω ἐπ' αὐτοῦ τρία σημεῖα τὰ Α Β Γ, καὶ ἤχθωσαν ἀπ' αὐτῶν ἐπὶ τὸ ὑποκείμενον ἐπίπεδον κάθετοι. ἀχθήσονται δὲ οὕτως· ἀπὸ τοῦ Γ προσπεσοῦσα εὐθεῖα πρὸς τὸ ὑποκείμενον ἐπίπεδον ὡς ἡ ΓΔ περιενηνέχθω καὶ ψαυέτω τοῦ ἐπιπέδου καθ' ἕτερα δύο σημεῖα τὰ Ε Ζ, καὶ εἰλήφθω τοῦ περὶ τὰ Δ Ε Ζ κύκλου κέντρον τὸ Κ· ἡ οὖν ἀπὸ τοῦ Γ κάθετος ἐπὶ τὸ Κ σημεῖον πεσεῖται, καὶ δοθὲν ἔσται τὸ Κ. ἤχθωσαν καὶ ἀπὸ τῶν Α Β κάθετοι ὁμοίως αἱ ΒΘ ΑΛ· ἐπιζευχθεῖσαι δὴ αἱ ΚΛ ΘΛ ἐκβεβλήσθωσαν, καὶ πεποιήσθω ὡς μὲν ἡ ΓΚ πρὸς ΑΛ, οὕτως ἡ ΚΜ πρὸς ΜΛ, ὡς δὲ ἡ ΒΘ πρὸς ΑΛ, οὕτως ἡ ΘΟ πρὸς ΟΛ [δοθέντα ἄρα τὰ Μ Ο ... ἐφ' ἡμῖν γάρ ἐστι τοιαύτας καθέτους λαβεῖν ὥστε ἐλαχίστην ἐν αὐταῖς εἶναι μίαν, ὡς τὴν ΑΛ]· εὐθεῖαι ἄρα αἱ ΜΑΓ ΒΑΟ. καὶ ἔσονται ἐν τῶι ἐπιπέδωι τοῦ ΑΒΓ κύκλου· ἡ ἄρα κοινὴ τομὴ αὐτοῦ καὶ τοῦ ὑποκειμένου ἐπιπέδου ἐστὶν ἡ ΜΟ. ἤχθω ἀπὸ τοῦ Λ ἐπὶ τὴν ΜΟ κάθετος ἡ ΛΝ, καὶ ἐπεζεύχθω ἡ ΑΝ· καὶ ἡ ΑΝ ἄρα κάθετος ἔσται ἐπὶ τὴν ΜΟ· πεπόρισται ἄρα καὶ ἡ ὑπὸ ΑΝΛ γωνία, τῶν ἐπιπέδων ἡ κλίσις.
35. ιθʹ. Τούτου προδειχθέντος ἔστω σφαῖρα μετέωρος, καὶ προκείσθω τό τε σημεῖον εὑρεῖν, ἐφ' ὃ πεσεῖται καθετικῶς ἐπὶ τὸ ὑποκείμενον ἐπίπεδον ἐνεχθεῖσα, καὶ τὴν ἐλαχίστην ἀποτεμνομένην ἀπὸ τῆς καθέτου μεταξὺ τῆς ἐπιφανείας καὶ τοῦ ἐπιπέδου.
Ἔστω ἡ σφαῖρα μετέωρος κειμένη περὶ κέντρον τὸ Ε, καὶ ἐν αὐτῆι μέγιστός τις ἐγγεγράφθω κύκλος ὁ ΑΒΓ· ἤτοι δὴ ἐν ὀρθῶι ἔσται ἐπιπέδωι πρὸς τὸ ὑποκείμενον ἢ οὔ, γνωσόμεθα δὲ οὕτως· λαβόντες ἐπὶ τῆς περιφερείας αὐτοῦ τρία τυχόντα σημεῖα καθέτους ἄξομεν ἐπὶ τὸ ὑποκείμενον ἐπίπεδον, ὡς μεμαθήκαμεν, κἂν μὲν τὰ σημεῖα ἐφ' ἃ πίπτουσιν αἱ κάθετοι ἐπ' εὐθείας ἀλλήλοις ὦσιν, ὀρθὰ πρὸς ἄλληλα ἔσται τὰ ἐπίπεδα, ἐὰν δὲ μή, κεκλιμένα.
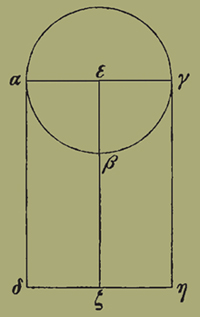
36. Ἔστω δὴ πρότερον ὀρθά, καὶ ἤχθωσαν ἀπὸ τῶν Α Γ σημείων κάθετοι αἱ ΑΔ ΓΗ· ἤτοι δὴ ἴσαι, ἔσονται ἢ οὔ.
Ἔστωσαν ἴσαι, καὶ τετμήσθω ἡ ΔΗ ἐπιζευχθεῖσα δίχα τῶι Ζ· ἔσται δὴ τὸ Ζ τὸ ζητούμενον σημεῖον ἐν τῶι ἐπιπέδωι, ἡ δὲ διχοτομία τῆς ΑΒΓ περιφερείας τὸ Β ἐπὶ τῆς ἐπιφανείας ἐφαρμόζον τῶι Ζ, καὶ ἡ ΒΖ ἐλαχίστη κάθετος, ὡς προείρηται.
37. κʹ. Μὴ ἔστωσαν δὲ ἴσαι αἱ κάθετοι, ἀλλὰ ἐλαχίστη ἡ ΑΔ, καὶ πεποιήσθω ὡς ἡ ΓΗ πρὸς ΑΔ, οὕτως ἡ ΗΘ πρὸς ΘΔ, ἐκβληθείσης τῆς ΗΔ· ἔσται δὴ τὸ Θ, καθ' ὃ ἡ ἀπὸ τοῦ Γ ἐπὶ τὸ Α συμπίπτει τῶι ὑποκειμένωι ἐπιπέδωι, καὶ δοθεῖσα ἔσται ἥ τε ΑΘ εὐθεῖα καὶ ἡ ὑπὸ ΑΘΔ γωνία. τούτων γενομένων ἐκκείσθω κύκλος ἴσος τῶι μεγίστωι περὶ διάμετρον τὴν ΚΛ, καὶ προσκείσθω ἡ ΛΜ ἴση τῆι ΑΘ, καὶ τῆι ὑπὸ ΑΘΔ γωνίαι ἴση συνεστάτω ἡ ὑπὸ ΚΜΝ, καὶ ἀπὸ τῶν Κ Λ κάθετοι αἱ ΛΟ ΚΝ, καὶ ἀπὸ τοῦ κέντρου ἡ ΣΠ, καὶ τῆι μὲν ΛΡ περιφερείαι ἴση ἀπειλήφθω ἡ ΑΒ, τῆι δὲ ΟΠ εὐθείαι ἴση ἡ ΔΖ [τὸ δὲ αὐτὸ ἦν λέγειν δίχα ἡ ΔΗ τῶι Ζ]. ἔσται οὖν τὸ μὲν Ζ σημεῖον, ἐφ' ὃ ἡ σφαῖρα καταφερομένη πεσεῖται, τὸ δὲ Β τὸ ἐπὶ τῆς ἐπιφανείας, ἡ δὲ ἐλαχίστη κάθετος ἡ ΒΖ.
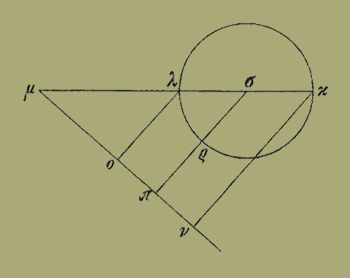
38. καʹ. Μὴ ἔστω δὲ ὁ ΑΒΓ κύκλος ἐν [ἑνὶ] ἐπιπέδωι ὀρθῶι πρὸς τὸ ὑποκείμενον, καὶ εἰλήφθω ἡ κοινὴ τῶν ἐπιπέδων τομὴ ἡ ΔΘ, καὶ εἰλήφθω ἐπὶ τοῦ ΑΒΓ κύκλου σημεῖα τὰ Α Γ κατὰ διάμετρον ἀλλήλοις κείμενα οὕτως ὥστε τὴν ἐπ' αὐτὰ ἐπιζευγνυμένην τὴν ΓΑ συμπίπτειν τῆι κοινῆι τομῆι τῆι ΔΘ [ἔστιν γὰρ ἐπ' ἐμοὶ διὰ τὸ τὴν ΔΘ ἐν τῶι τοῦ ΑΒΓ κύκλου ἐπιπέδωι εἶναι]. συμπιπτέτω κατὰ τὸ Θ· δοθεῖσα ἄρα ἡ ΑΘ καὶ ἡ Θ γωνία. 39. ἤχθω ἀπὸ τοῦ Ε κέντρου κάθετος ἐπὶ τὴν ΔΘ ἡ ΕΒΔ. ἀχθήσεται οὕτως· ἐκκείσθω κύκλος ὁ ΗΖΛ ἴσος τῶι μεγίστωι τῶι ΑΒΓ περὶ διάμετρον τὴν ΖΗ, καὶ προσκείσθω ἡ ΗΚ ἴση τῆι ΓΘ, καὶ τῆι ὑπὸ ΑΘΔ γωνίαι ἴση
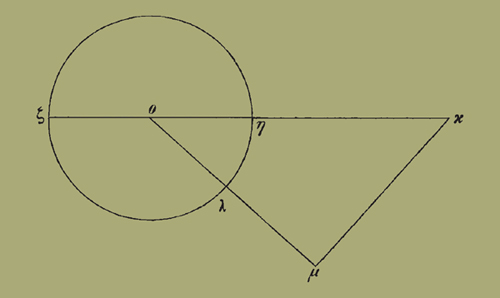
συνεστάτω ἡ ὑπὸ ΖΚΜ, καὶ ἀπὸ τοῦ Ο κέντρου κάθετος ἡ ΟΛΜ, καὶ τῆι μὲν ΗΛ περιφερείαι ἴση ἀπειλήφθω ἡ ΓΒ, τῆι δὲ ΚΜ εὐθείαι ἡ ΘΔ· ἡ ΔΒ ἄρα ἴση ἐστὶν τῆι ΜΛ καὶ κάθετός ἐστιν ἐπὶ τὴν ΔΘ καὶ ἐκβαλλομένη ἐπὶ τὸ Ε κέντρον πίπτει· ταῦτα γὰρ δῆλα ἐκ τῆς ὁμοιότητος. ἤχθω δὴ τῆι ΔΘ πρὸς ὀρθὰς ἐν τῶι ὑποκειμένωι ἐπιπέδωι ἡ ΔΙ· ἡ ΔΘ ἄρα ὀρθὴ πρὸς τὸ διὰ τῶν Ε Δ Ι ἐπίπεδον, ὥστε καὶ ὁ ΑΒΓ κύκλος ὀρθὸς πρὸς τὸ διὰ τῶν Ε Δ Ι ἐπίπεδον· ἐκβληθὲν ἄρα τὸ διὰ τῶν Ε Δ Ι ἐπίπεδον κύκλον ποιήσει ἐν τῆι σφαίραι μέγιστον ὀρθὸν πρὸς τὸν ΑΒΓ διὰ τῶν πόλων αὐτοῦ πίπτοντα καὶ διὰ τῶν Β Ο σημείων, ὥστε, ἐὰν τοῦ ΑΒΓ τὸν πόλον λαβόντες τὸν Π διὰ τοῦ Π καὶ ἑκατέρου τῶν Β Ο γράψωμεν κύκλον, οὗτος ἔσται ὁ γινόμενος μέγιστος ἐν τῆι σφαίραι [ὑπὸ τοῦ διὰ τῶν Ο Δ Ι ἐπιπέδου]. γεγράφθω ὁ ΒΠΟ, καὶ ἐκκείσθω πάλιν κύκλος ὁ ΡΝΤ
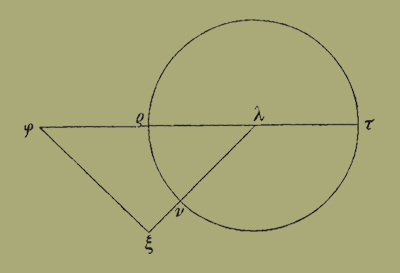
περὶ διάμετρον τὴν ΡΤ, καὶ προσκείσθω ἡ ΡΦ ἴση τῆι ΒΔ, καὶ τῆι ὑπὸ ΒΔΙ γωνίαι ἴση ἡ ὑπὸ ΡΦΞ, καὶ ἀπὸ τοῦ Λ κέντρου κάθετος ἡ ΛΝΞ, καὶ τῆι μὲν ΡΝ περιφερείαι ἴση ἀπειλήφθω ἐπὶ τοῦ ΠΒΟ κύκλου ἡ ΒΥ, τῆι δὲ ΦΞ ἴση ἡ ΔΙ, καὶ ἐπεζεύχθω ἡ ΙΥ· ἡ ΙΥ ἄρα ἴση ἔσται τῆι ΞΝ καὶ ἐκβαλλομένη ἐπὶ τὸ Ε κέντρον πεσεῖται καὶ ἔσται κάθετος ἐπὶ τὸ ὑποκείμενον ἐπίπεδον, ἐπεὶ καὶ ἐπὶ τὴν ΙΔ· τὸ μὲν ἄρα Ι σημεῖον ἔσται ἐφ' ὃ πίπτει ἡ σφαῖρα, τὸ δὲ Υ καθ' ὃ πίπτει, ἡ δὲ ἐλαχίστη κάθετος ἡ ΙΥ.
40. κβʹ. Σφαίρας ὑποκειμένης καὶ σημείου δοθέντος ἐκτὸς αὐτῆς, εὑρεῖν τὸ σημεῖον καθ' ὃ ἡ ἀπὸ τοῦ δοθέντος ἐπὶ τὸ κέντρον ἐπιζευγνυμένη τέμνει τὴν ἐπιφάνειαν.
Ἔστιν δὲ φανερόν· ἂν γὰρ ἡτισοῦν ἀπὸ τοῦ δοθέντος εὐθεῖα προσπεσοῦσα πρὸς τὴν ἐπιφάνειαν περιενεχθῆι, καὶ αὕτη γράψει κύκλον καὶ πόλος αὐτοῦ τὸ ζητούμενον ἔσται σημεῖον.
41. Ὑποκείσθω πάλιν ἡ σφαῖρα, καὶ δύο σημεῖα δεδόσθω τῆς ἐπιφανείας ἐκτὸς ἀμφότερα, καὶ προκείσθω τὰ σημεῖα λαβεῖν καθ' ἃ ἡ ἐπὶ τὰ δοθέντα ἐπιζευγνυμένη τέμνει τὴν ἐπιφάνειαν.
Κείσθω γὰρ ἡ σφαῖρα περὶ κέντρον τὸ Β, καὶ τὰ δοθέντα σημεῖα ἐκτὸς ἔστω τὰ Α Γ, καὶ καθ' ἃ συμβάλλουσιν τῆι ἐπιφανείαι αἱ ἀπὸ τῶν Α Γ ἐπὶ τὸ Β ἐπιζευγνύμεναι εἰλήφθω σημεῖα τὰ Δ Ε, δι' ὧν γεγράφθω μέγιστος κύκλος ὁ ΔΕΖΗ· δοθεῖσαι ἄρα αἱ ΑΔ ΓΕ (λῆμμα γάρ)· καὶ διὰ τὸ δεδόσθαι τὴν ἐκ τοῦ κέντρου τῆς σφαίρας καὶ ὅλαι δοθήσονται αἱ ΑΒ ΓΒ. ἔστιν δὲ καὶ ἡ τὰ δοθέντα ἐπιζευγνύουσα ἡ ΑΓ δοθεῖσα. ἐκ τριῶν οὖν τῶν ΑΒ ΑΓ ΓΒ τρίγωνον συνεστάτω τὸ ΘΚΛ, καὶ περὶ κέντρον τὸ Θ γεγράφθω κύκλος ἴσος τῶι ΕΔΖΗ ὁ ΣΜΝΟ. ἐὰν μὲν οὗτος τέμνηι τὴν ΚΛ, δῆλον ὅτι καὶ ἡ ἐπὶ τὰ Α Γ ἐπιζευγνυμένη τέμνει τὴν σφαῖραν, εἰ δὲ μή, οὐ τέμνει. τεμνέτω οὖν ὁ κύκλος τὴν ΚΛ κατὰ τὰ Μ Ν, καὶ τῆι μὲν ΣΜ περιφερείαι ἴση ἀπειλήφθω ἡ ΔΗ, τῆι δὲ ΟΝ ἡ ΕΖ. φανερὸν δὴ ὅτι τὰ Η Ζ σημεῖα ἔσται καθ' ἃ τέμνει ἡ ἐπιζευγνύουσα τὰ Α Γ σημεῖα τὴν τῆς σφαίρας ἐπιφάνειαν.
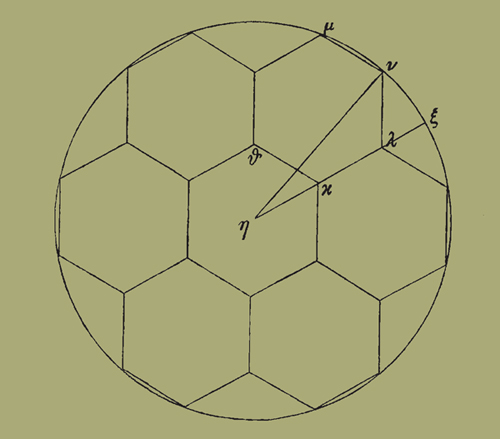
42. κγʹ. Χρήσιμα καὶ τὰ ἐν τοῖς ἰδίως λεγομένοις ὀργανικοῖς καὶ μάλισθ' ὅταν ἐπὶ τὸ εὔκολον ὑπὸ τῆς ἀναλύσεως χειραγωγούμενα τὴν ἀνάλογον πεῖραν διαφεύγειν δύνηται, οἷον εἰς τὸν δοθέντα κύκλον ἑπτὰ ἑξάγωνα ἐγγράψαι, τὸ μὲν περὶ τὸ αὐτὸ κέντρον τῶι κύκλωι, τὰ δὲ λοιπὰ ἓξ ἀπὸ μὲν τῶν τοῦ μέσου πλευρῶν ἀναγεγραμμένα, τὰς δὲ ἀντικειμένας πλευρὰς ἔχοντα ἐνηρμοσμένας ἑκάστην εἰς τὴν τοῦ κύκλου περιφέρειαν.
Ἔστω ὁ δοθεὶς κύκλος περὶ κέντρον τὸ Η, καὶ κείσθω περὶ τὸ αὐτὸ κέντρον ἑξαγώνου πλευρὰ ἡ ΘΚ, ὥστε ἔσται τὸ ἀπὸ τῆς ΘΚ ἀναγραφὲν ἑξάγωνον τὴν ΜΝ πλευρὰν ἔχον ἐνηρμοσμένην τῆι τοῦ κύκλου περιφερείαι, καὶ ἐπεζεύχθω ἡ ΗΚ· ἐπ' εὐθείας ἄρα ἐστὶν τῆι ΚΛ πλευρᾶι τοῦ ἑξαγώνου, διὰ τὸ διμοίρου μὲν εἶναι τὴν ὑπὸ ΗΚΘ, ὀρθῆς δὲ καὶ τρίτου τὴν ὑπὸ ΘΚΛ. ἐπεζεύχθω ἡ ΗΝ. ἐπεὶ ἴσαι αἱ ΗΚ ΚΛ, διπλῆ ἐστὶν ἡ ΗΛ τῆς ΛΝ. καὶ δοθεῖσα ἡ Λ γωνία [ὀρθῆς γὰρ καὶ τρίτου]· δοθὲν ἄρα τὸ ΝΛΗ τρίγωνον τῶι εἴδει· λόγος ἄρα τῆς ΗΝ πρὸς ΝΛ δοθείς. καὶ δοθεῖσα ἡ ΗΝ· δοθεῖσα ἄρα καὶ ἡ ΝΛ πλευρὰ τοῦ ἑξαγώνου.
43. Τὸ δὲ ὀργανικὸν οὕτως· ἐκκείσθω τῆς ἐκ τοῦ κέντρου τοῦ κύκλου τρίτον μέρος ἡ ΑΓ, καὶ ἐπ' αὐτῆς τμῆμα κύκλου τὸ ΑΒΓ γωνίαν δεχόμενον διμοίρου ὀρθῆς, καὶ οἵων ἐστὶν ἡ ΑΓ εʹ, τοιούτων δʹ ἀπειλήφθω ἡ ΓΕ, καὶ ἤχθω ἐφαπτομένη ἡ ΒΕ· λέγω ὅτι ἡ ΑΒ ἐπιζευχθεῖσα ἴση ἐστὶν τῆι ΘΚ τοῦ ἑξαγώνου πλευρᾶι.
Ἐκβεβλήσθω ἡ ΒΓ, καὶ τῆι ΑΒ ἴση ἀφηιρήσθω ἡ ΒΔ· ἰσόπλευρον ἄρα τὸ ΑΒΔ. καὶ τῆι ἐκ τοῦ κέντρου τοῦ κύκλου ἴση ἡ ΑΖ. ἐπεὶ ἡ ΑΕ πρὸς ΕΓ λόγον ἔχει ὃν τὰ θʹ πρὸς δʹ, ἕξει καὶ τὸ ἀπὸ ΑΒ πρὸς τὸ ἀπὸ ΒΓ τὸν αὐτὸν λόγον· ἡμιολία ἄρα ἡ ΑΒ, τουτέστιν ἡ ΒΔ, τῆς ΒΓ· διπλῆ ἄρα ἡ ΒΓ τῆς ΓΔ. ἀλλὰ καὶ ἡ ΖΓ τῆς ΓΑ· καὶ ἡ ΒΖ ἄρα ἐπιζευχθεῖσα τῆς ΑΔ, τουτέστιν τῆς ΑΒ, ἐστὶν διπλῆ. ἦν δὲ καὶ ἡ ΗΛ τῆς ΛΝ διπλῆ, καὶ ἴσας περιέχουσιν γωνίας· ὅμοιον ἄρα τὸ ΑΒΖ τρίγωνον τῶι ΝΛΗ τριγώνωι. καὶ ἔστιν ἴση ἡ ΑΖ τῆι ΝΗ· ἴση ἄρα καὶ ἡ ΑΒ τῆι ΛΝ ἢ τῆι ΘΚ.
Τὸ αὐτὸ ἄλλως σαφέστερον.
44. κδʹ. Ἔστω τῆι ἐκ τοῦ κέντρου τοῦ δοθέντος κύκλου ἴση ἡ ΑΖ, καὶ ἀπειλήφθω αὐτῆς τὸ γʹ μέρος, καὶ ἔστω ἡ ΑΓ, ἐφ' ἧς τμῆμα κύκλου γεγράφθω τὸ ΑΒΓ δεχόμενον γωνίαν διμοίρου ὀρθῆς, καὶ οἵων ἐστὶν ἡ ΑΓ εʹ, τοιούτων δʹ ἀπειλήφθω ἡ ΓΕ, καὶ ἤχθω ἐφαπτομένη τοῦ τμήματος ἡ ΕΒ, καὶ ἐπεζεύχθω ἥ τε ΑΒ καὶ ἡ ΖΒ, καὶ ἔτι ἐπιζευχθεῖσα ἡ ΒΓ ἐκβεβλήσθω ἐπὶ τὸ Δ, καὶ κείσθω τῆι ΑΒ ἴση ἡ ΒΔ, καὶ ἐπεζεύχθω ἡ ΑΔ. ἐπεὶ οὖν εἰς κύκλον διήχθησαν ἥ τε ΕΓΑ καὶ ἡ ΕΒ, καὶ ἡ μὲν τέμνει τὸν κύκλον ἡ δὲ ἐφάπτεται, τὸ ἄρα ὑπὸ ΑΕΓ ἴσον ἐστὶν τῶι ἀπὸ τῆς ΕΒ· ἔστιν ἄρα ὡς ἡ ΑΕ πρὸς ΕΒ, οὕτως ἡ ΒΕ πρὸς ΓΕ· ἰσογώνιον ἄρα τὸ ΓΒΕ τρίγωνον τῶι ΑΒΕ τριγώνωι. ἔστιν ἄρα ὡς ἡ ΕΑ πρὸς ΑΒ, ἡ ΕΒ πρὸς ΒΓ· καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ἀπὸ τῆς ΕΒ, τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΓ. ἀλλ' ὡς τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ἀπὸ τῆς ΕΒ, οὕτως ἐστὶν ἡ ΑΕ πρὸς ΕΓ διὰ κʹ τοῦ ςʹ. καὶ ὡς ἄρα ἡ ΑΕ πρὸς ΕΓ, οὕτως τὸ ἀπὸ τῆς ΑΒ, τουτέστιν τὸ ἀπὸ τῆς ΒΔ, πρὸς τὸ ἀπὸ τῆς ΒΓ· τὸ ἄρα ἀπὸ τῆς ΒΔ πρὸς τὸ ἀπὸ τῆς ΒΓ λόγον ἔχει ὃν τὰ θʹ πρὸς δʹ· ἡμιολία ἄρα ἡ ΒΔ τῆς ΒΓ· διπλασία ἄρα ἡ ΒΓ τῆς ΓΔ. ἔστιν δὲ καὶ ἡ ΖΓ τῆς ΓΑ διπλασία· ὡς ἄρα ἡ ΖΓ πρὸς ΓΑ, ἡ ΒΓ πρὸς ΓΔ. καὶ ἴσαι εἰσὶν αἱ πρὸς τῶι Γ γωνίαι· ἴση ἄρα καὶ ἡ μὲν Δ γωνία τῆι ὑπὸ ΖΒΓ, ἡ δὲ Ζ τῆι ὑπὸ ΓΑΔ· ἔστιν ἄρα ὡς ἡ ΖΒ πρὸς ΒΓ, οὕτως ἡ ΑΔ πρὸς ΔΓ. ἐναλλὰξ ὡς ἡ ΖΒ πρὸς ΑΔ, οὕτως ἡ ΒΓ πρὸς ΓΔ. διπλασία δὲ ἡ ΒΓ τῆς ΓΔ· διπλασία ἄρα καὶ ἡ ΖΒ τῆς ΑΔ, τουτέστιν τῆς ΑΒ. καὶ ἔστιν διμοίρου ἡ Δ· διμοίρου ἄρα ὀρθῆς καὶ ἡ ὑπὸ ΖΒΓ. ὅλη δὲ ἡ ὑπὸ ΑΒΖ μιᾶς ὀρθῆς καὶ γʹ. ἐὰν οὖν ἔχωμεν κύκλον, οὗ κέντρον τὸ Η, ἴσην ἔχοντα τὴν ἐκ τοῦ κέντρου τῆι ΑΖ εὐθείαι, καὶ διαγάγωμεν ἀπὸ τοῦ κέντρου αὐτοῦ τὴν ΗΞ εὐθεῖαν, καὶ ἴσην θῶμεν τῆι ΖΒ τὴν ΗΛ εὐθεῖαν, καὶ πρὸς τῆι ΗΛ εὐθείαι καὶ τῶι Λ σημείωι ἴσην γωνίαν συστησώμεθα τὴν ὑπὸ ΗΛΝ τῆι ὑπὸ ΖΒΑ, καὶ ἐπιζεύξωμεν τὴν ΗΝ, ἰσογώνιον γίνεται τὸ ΗΛΝ τρίγωνον τῶι ΑΖΒ τριγώνωι. καὶ ἔστιν ἡ ΑΖ ἴση τῆι ΗΝ· ἴση ἄρα καὶ ἡ ΝΛ τῆι ΑΒ. καὶ φανερὸν ὅτι ἀπὸ τῆς ἴσης τῆι ΑΒ εὐθείας γίνεται ἡ τῶν ζʹ εἰς τὸν κύκλον ἑξαγώνων ἐγγραφή.
45. κεʹ. Πῶς δὲ καὶ ἡ τῶν προειρημένων τυμπάνων γίνεται παράθεσις, νῦν ἐροῦμεν.
Ἔστω γὰρ δύο τύμπανα ἔντορνα καὶ παρακείμενα ἀλλήλοις τὰ Α Β, καὶ ἔστω ὡς ἡ διάμετρος τοῦ Α πρὸς τὴν διάμετρον τοῦ Β, οὕτως τὸ πλῆθος τῶν ὀδόντων τοῦ Α πρὸς τὸ πλῆθος τῶν ὀδόντων τοῦ Β· οὕτως γὰρ ἡ παράθεσις τῶν τυμπάνων σώιζεται διὰ τὸ εἶναι ὡς τὴν περίμετρον τοῦ κύκλου πρὸς τὴν περίμετρον, οὕτως τὴν διάμετρον πρὸς τὴν διάμετρον (τοῦτο γὰρ ἑξῆς). ὑποκείσθω δὴ τὸ μὲν Α ὀδόντων ξʹ, τὸ δὲ Β ὀδόντων μʹ· λέγω ὅτι ἐστὶν ὡς τὸ τάχος τοῦ Α πρὸς τὸ τάχος τοῦ Β, οὕτως τὸ πλῆθος τῶν ὀδόντων τοῦ Β πρὸς τὸ πλῆθος τῶν ὀδόντων τοῦ Α.
Ἐπεὶ γὰρ παράκειται ἀλλήλοις τὰ Α Β, ὅσους ἂν ὀδόντας κινηθῆι τὸ Β, τοσούτους ὀδόντας κινηθήσεται καὶ τὸ Α· ὅταν ἄρα τὸ Β στρεφόμενον μίαν ἀποκατάστασιν ποιήσηται, τότε τὸ Α μʹ ὀδόντας κινηθήσεται, ὥστε καί, ὅταν τὸ Β ξʹ ἀποκαταστάσεις ποιήσηται, ὅσον ἐστὶν τὸ πλῆθος τῶν ὀδόντων τοῦ Α, τότε τὸ Α ὀδόντας κινηθήσεται ͵βυʹ, ὅσον ἐστὶν τὸ πλῆθος τῶν ὀδόντων τοῦ Α ἐπὶ τὸ πλῆθος τῶν ὀδόντων τοῦ Β. ὁμοίως δὲ δειχθήσεται καί, ὅταν τὸ Α μʹ ἀποκαταστάσεις ποιήσηται, ὅσον ἐστὶν τὸ πλῆθος τῶν ὀδόντων τοῦ Β, τότε τὸ Β ὀδόντας κεκινημένον ͵βυʹ, ὅσον ἐστὶν τὸ πλῆθος τῶν ὀδόντων τοῦ Β ἐπὶ τὸ πλῆθος τῶν ὀδόντων τοῦ Α· ὅταν ἄρα τὸ Α ἀποκαταστάσεις ποιήσηται μʹ, ὅσον ἐστὶν τὸ πλῆθος τῶν ὀδόντων τοῦ Β, τότε καὶ τὸ Β ἀποκαταστάσεις ποιεῖται ξʹ, ὅσον ἐστὶν τὸ πλῆθος τῶν ὀδόντων τοῦ Α· ἔστιν ἄρα ὡς τὸ τάχος τοῦ Α πρὸς τὸ τάχος τοῦ Β, οὕτως τὸ πλῆθος τῶν ὀδόντων τοῦ Β πρὸς τὸ πλῆθος τῶν ὀδόντων τοῦ Α.
46. κςʹ. Ὅτι δὲ αἱ τῶν κύκλων περιφέρειαι πρὸς ἀλλήλας εἰσὶν ὡς αἱ διάμετροι, νῦν δείξομεν.
Ἔστωσαν γὰρ δύο κύκλοι οἱ ΑΒ ΓΔ, καὶ διάμετροι αὐτῶν αἱ ΑΒ ΓΔ· λέγω ὅτι ἐστὶν ὡς ἡ τοῦ ΑΒ κύκλου περιφέρεια πρὸς τὴν τοῦ ΓΔ κύκλου περιφέρειαν, οὕτως ἡ ΑΒ διάμετρος πρὸς τὴν ΓΔ.
Ἐπεὶ γάρ ἐστιν ὡς ὁ ΑΒ κύκλος πρὸς τὸν ΓΔ κύκλον, οὕτως τὸ ἀπὸ τῆς ΑΒ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΓΔ τετράγωνον, ἀλλὰ τοῦ μὲν ΑΒ κύκλου τετραπλάσιόν ἐστιν τὸ περιεχόμενον ὀρθογώνιον ὑπό τε τῆς ΑΒ διαμέτρου καὶ τῆς τοῦ ΑΒ περιφερείας, τοῦ δὲ ΓΔ κύκλου τετραπλάσιόν ἐστιν τὸ ὑπὸ τῆς ΓΔ καὶ τῆς τοῦ ΓΔ περιφερείας (τὸ γὰρ ὑπὸ τῆς ἐκ τοῦ κέντρου τοῦ κύκλου καὶ τῆς περιμέτρου τοῦ κύκλου περιεχόμενον ὀρθογώνιον διπλάσιόν ἐστιν τοῦ ἐμβαδοῦ τοῦ κύκλου, ὡς Ἀρχιμήδης, καὶ ὡς ἐν τῶι εἰς τὸ πρῶτον τῶν μαθηματικῶν σχολίωι δέδεικται καὶ ὑφ' ἡμῶν δι' ἑνὸς θεωρήματος), καὶ ὡς ἄρα τὸ ὑπὸ τῆς ΑΒ καὶ τῆς περιφερείας τοῦ ΑΒ πρὸς τὸ ὑπὸ τῆς ΓΔ καὶ τῆς τοῦ ΓΔ κύκλου περιφερείας, οὕτως τὸ ἀπὸ τῆς ΑΒ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΓΔ. καὶ ἐναλλὰξ ὡς τὸ ὑπὸ τῆς τοῦ ΑΒ κύκλου περιφερείας καὶ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΑΒ, οὕτως τὸ ὑπὸ τῆς τοῦ ΓΔ κύκλου περιφερείας καὶ τῆς ΓΔ πρὸς τὸ ἀπὸ τῆς ΓΔ· καὶ ὡς ἄρα ἡ τοῦ ΑΒ κύκλου περιφέρεια πρὸς τὴν ΑΒ, οὕτως ἡ τοῦ ΓΔ περιφέρεια πρὸς τὴν ΓΔ (τοῦτο γὰρ πρῶτόν ἐστιν ἐν τῶι ςʹ λαμβανόμενον), καὶ ἐναλλὰξ ὡς ἡ τοῦ ΑΒ περιφέρεια πρὸς τὴν τοῦ ΓΔ περιφέρειαν, οὕτως ἡ ΑΒ πρὸς τὴν ΓΔ.
47. κζʹ. Τυμπάνου δοθέντος καὶ τοῦ πλήθους τῶν ὀδόντων αὐτοῦ, ἐπιτετάχθω παραθεῖναι αὐτῶι τύμπανον δοθὲν ἔχον τὸ πλῆθος τῶν ὀδόντων καὶ εὑρεῖν τὴν διάμετρον τοῦ παρατιθεμένου τυμπάνου.
Ἔστω τύμπανον τὸ Α, οὗ τὸ πλῆθος τῶν ὀδόντων ἔστω ὁ Β ἀριθμὸς [μονάδων ξʹ], καὶ παρακείσθω τῶι Α τὸ Γ τύμπανον, οὗ τὸ πλῆθος τῶν ὀδόντων ἔστω ὁ Δ ἀριθμὸς [μονάδων μʹ]· δεῖ δὴ τοῦ Γ τὴν διάμετρον εὑρεῖν.
Ἐπεὶ οὖν ὁ Β ἀριθμὸς πλῆθός ἐστιν ὀδόντων τοῦ Α, ὁ δὲ Δ πλῆθός ἐστιν ὀδόντων τοῦ Γ [καὶ ἔστιν τὸ μὲν πλῆθος τῶν ὀδόντων τοῦ Α ἡ περίμετρος αὐτοῦ, τὸ δὲ πλῆθος τῶν ὀδόντων τοῦ Γ ἡ περίμετρος αὐτοῦ], ἔστιν ἄρα ὡς ὁ Β ἀριθμὸς πρὸς τὸν Δ, οὕτως ἡ περίμετρος τοῦ Α πρὸς τὴν περίμετρον τοῦ Γ. ὡς δὲ ἡ περίμετρος πρὸς τὴν περίμετρον, οὕτως ἡ διάμετρος πρὸς τὴν διάμετρον. λόγος δὲ τοῦ Β ἀριθμοῦ πρὸς τὸν Δ ἀριθμὸν δοθείς [ἔστιν γὰρ ὁ τῶν ξʹ πρὸς τὰ μʹ]· λόγος ἄρα καὶ τῆς διαμέτρου τοῦ Α πρὸς τὴν διάμετρον τοῦ Γ δοθείς [ὁ τῶν ξʹ πρὸς τὰ μʹ]. καὶ ἔστιν δοθεῖσα ἡ διάμετρος τοῦ Α· δοθεῖσα ἄρα καὶ ἡ διάμετρος τοῦ Γ [δεῖ γὰρ ποιεῖν ὡς τὸν ξʹ ἀριθμὸν πρὸς τὸν μʹ, οὕτως τὴν διάμετρον τοῦ Α πρὸς ἄλλην τινά, καὶ ὁ περὶ διάμετρον ἐκείνην γραφόμενος κύκλος ἴσος ἔσται τῶι ζητουμένωι τυμπάνωι].
48. Ὀργανικῶς δὲ οὕτως· ἐκκείσθω τις εὐθεῖα ἡ ΕΖ τετμημένη εἰς ἴσα, ἴσα τὸ πλῆθος τοῖς ὀδοῦσι τοῦ Α τυμπάνου [τουτέστιν ξʹ], καὶ πρὸς ὀρθὰς αὐτῆι ἀχθεῖσα κείσθω διαμέτρωι τοῦ Α τυμπάνου ἴση ἡ ΖΗ, καὶ ἐπεζεύχθω ἡ ΕΗ, καὶ [οἵων ἡ ΕΖ ξʹ, τοιούτων μʹ] ἀπειλήφθω ἡ ΕΘ τοῦ πλήθους τῶν ὀδόντων τοῦ Γ γινομένη, καὶ διὰ τοῦ Θ παράλληλος τῆι ΖΗ ἤχθω ἡ ΘΚ· καὶ ἔσται ἄρα ἡ ΘΚ ἴση τῆι διαμέτρωι τοῦ Γ τυμπάνου (φανερὰ γὰρ ἡ ἀπόδειξις).
49. κηʹ. Πῶς δὲ κατασκευάζεται κοχλίας τὴν ἕλικα ἁρμοστὴν ἔχων τοῖς λοξοῖς ὀδοῦσι τοῦ δοθέντος τυμπάνου, φανερὸν οὕτως ἔσται.
Νοείσθω κύλινδρος ἰσοπαχῶς τετορνευμένος ὁ ΑΔΕΖ, πλευρὰ δ' αὐτοῦ ἡ ΑΕ, καὶ εἰλήφθω μονοστρόφου ἕλικος ἐπ' αὐτῆς διάστημα τὸ ΑΒ, καὶ λεπίδιον χαλκοῦν γεγενήσθω, οὗ τὸ μὲν ΗΘΚ μέρος τρίγωνον ὀρθογώνιον ἔστω ὀρθὴν ἔχον τὴν Θ γωνίαν, τὸ δὲ λοιπὸν παραλληλόγραμμον ὀρθογώνιον τὸ ΘΚΛ, ἴση δὲ κείσθω ἡ ΘΗ τῆι ΑΒ, ἡ δὲ ΘΚ τῆι περιμέτρωι τοῦ ΑΔΕΖ κυλίνδρου, καὶ περικαμπτέσθω τὸ λεπίδιον περὶ τὸν κύλινδρον, ἵνα καὶ τὸ ΘΚΛ παραλληλόγραμμον κύλινδρος γένηται ἁπτόμενος τοῦ ΔΕ, ὅταν εἰσαχθῆι, καὶ κείσθω τὸ μὲν Θ ἐπὶ τὸ Α, τὸ δὲ Η ἐπὶ τὸ Β, καὶ οὕτως γράψομεν διὰ τῆς ΗΚ ὑποτεινούσης καμφθείσης [δὲ] τὴν καλουμένην μονόστροφον ἕλικα ὡς τὴν ΒΑ. καὶ πάλιν μεταθέντες τὸ λεπίδιον, ὥστε τὸ μὲν Θ κατὰ τὸ Β εἶναι τὸ δὲ Η κατὰ τὸ Γ, γράψομεν διὰ τῆς ΗΚ ἑτέραν ἕλικα μονόστροφον, ὥστε τὴν ὅλην εἶναι δίστροφον. ἐν ὧι γὰρ χρόνωι τὸ Α ἐπὶ τὸ Β παραγίνεται ὁμαλῶς κινούμενον, ἐν τούτωι καὶ ἡ ΑΒ κατὰ τῆς ἐπιφανείας τοῦ κυλίνδρου κινηθεῖσα εἰς τὸ αὐτὸ ἀποκαθίσταται καὶ τὸ εἰρημένον φέρεσθαι σημεῖον κατὰ τῆς ΑΒ εὐθείας γράψει τὴν μονόστροφον ἕλικα· τοῦτο γὰρ Ἀπολλώνιος ὁ Περγεὺς ἀπέδειξεν. [ἐὰν οὖν καὶ ἑκατέραν τῶν ΑΒ ΒΓ καὶ τὰς ἑξῆς ἄχρι τοῦ Ε δίχα τέμνωμεν καὶ διὰ τῶν σημείων τῶι λεπιδίωι γράψωμεν μονοστρόφους ἕλικας ἀπ' αὐτῶν κατὰ τὸ βάθος τῆς ἕλικος ὃ βουλόμεθα λάβωμεν καὶ ἀπὸ τοῦ βάθους λοιπὸν καὶ τῆς γραφείσης ἕλικος, ῥαιδίως τὴν ἕλικα φακοειδῆ ῥινήσαντες ἕξομεν ἀπηρτισμένην.]
50. κθʹ. Πάλιν νοείσθω ἐν τῆι ἑτέραι ἐπιφανείαι τοῦ δοθέντος τυμπάνου περὶ τὸν κότραφον κύκλος, οὗ περιφέρεια ἡ ΡΥΤ κέντρον δὲ τὸ Ξ, καὶ τὰ Ρ Υ Τ ἴσον ἀπ' ἀλλήλων ἀπέχοντα, λόγου χάριν τοῦ πανὸς κύκλου εἰς εἴκοσι τέσσαρα διηιρημένου, καὶ ἀπὸ τῶν Ρ Υ Τ ἐπὶ τὸ Ξ κέντρον νεύουσαι διήχθωσαν ἄχρι τοῦ περὶ τὸ Ξ κέντρον γεγραμμένου κύκλου τοῦ ΜΝΠΦ αἱ ΡΟ ΥΟ ΤΟ, καὶ ἀπὸ τῶν διχοτομούντων τὰς ΟΟ περιφερείας σημείων διήχθωσαν ἐπὶ τὰ Ρ Υ Τ σημεῖα αἱ ΜΡ ΝΡ ΝΥ ΠΥ ΠΤ ΤΦ, καὶ ἀπὸ τῆς ΟΡ εὐθείας προήχθω ἐν τῆι κυρτῆι τοῦ τυμπάνου ἐπιφανείαι ἡ ΡΣ μέχρι τῆς περιφερείας οὖσα τοῦ ἐν τῆι ἑτέραι ἐπιφανείαι τοῦ τυμπάνου περὶ τὸν κότραφον ὁμοίως γραφομένου τοῦ ΧΩ κύκλου, καὶ ἀπὸ τοῦ Σ τῆι μὲν ἡμισείαι τῆς ΡΥ περιφερείας [ὡς λοξώσεως] ἴση κείσθω ἡ ΣΧ, τῆι δὲ ΡΥ ἡ ΧΩ, καὶ οὕτως ἑξῆς ἴσην θέντες τῆι ΥΤ τὴν ΩΨ καὶ τὰς λοιπάς, καὶ ἐπιζεύξαντες τὰς ΡΧ ΥΩ ΤΨ ἕξομεν τὰς τῶν ὀδόντων λοξώσεις. καὶ ἐπεὶ ἴσος ἐστὶν ὁ ΡΥ κύκλος τῶι ΧΩ κύκλωι, γράψομεν κἀν τῆι ἑτέραι ἐπιφανείαι τοῦ τυμπάνου περὶ κέντρον τὸ ἀντικείμενον τῶι Ξ σημείωι κύκλον ἴσον τῶι ΜΝ, καὶ ἀπὸ τῶν Χ Ω ἀγαγόντες ἐπ' αὐτὸν εὐθείας νευούσας ἐπὶ τὸ κέντρον αὐτοῦ, καὶ τὰ αὐτὰ ποιήσαντες τοῖς ἐπὶ τῆς ΡΥΤ περιφερείας [τοῦ κύκλου] ἕξομεν καὶ τὴν ἄλλην πλευρὰν τοῦ τυμπάνου καταγεγραμμένην. καὶ λοιπὸν ἐκκόψαντες τὰ μεταξὺ τῶν γραμμῶν σχήματα ὡς τὰ ΝΡΥ ΥΠΤ καὶ τὰ ἀντικείμενα ἕξομεν τὸ τύμπανον ὠδοντωμένον ὀδοῦσιν λοξοῖς. ἐμβαίνει δὲ ἕκαστος εἰς τὴν τοῦ κοχλίου ἕλικα, ἐπεὶ καὶ τὸ μεταξὺ διάστημα τὸ ΡΥ ἴσον ἐστὶν τῶι ΑΒ διαστήματι τῆς τοῦ κοχλίου ἕλικος. καὶ δῆλον ὡς καθ' ἑκάστην στροφὴν τοῦ κοχλίου εἷς ὀδοὺς παρενεχθήσεται· τοῦτο γὰρ Ἥρων ἀπέδειξεν ἐν τοῖς μηχανικοῖς, γραφήσεται δὲ καὶ ὑφ' ἡμῶν, ἵνα μηδὲν ἔξωθεν ἐπιζητῶμεν.
51. λʹ. Νοείσθω γὰρ κοχλίας ὁ ΑΒ, ἡ δὲ ἐν αὐτῶι ἕλιξ ἡ ΑΓΔΕΖΒ [νοείσθωσαν δὲ μονόστροφοι αἱ εἰρημέναι ἕλικες], τύμπανον δὲ ἔστω [τὸ] παρακείμενον καὶ ὠδοντωμένον τὸ ΗΓΕΘ ὀδόντας ἔχον τοὺς ΗΓ ΓΕ ΕΘ ἁρμόζοντας τῆι ἕλικι [οἱ ἄρα λοιποὶ οὐκ ἐναρμόσουσιν εἰς τὰς λοιπὰς ἕλικας]. ἐὰν οὖν ἐπιστρέφωμεν τὸν κοχλίαν, ὥστε τὸ Ε σημεῖον παρωθεῖσθαι ἐπὶ τὰ Γ μέρη, παρέσται τὸ Ε ἐπὶ τὸ Γ, ὅταν ὁ κοχλίας ἀποκατάστασιν μίαν ποιήσηται, καὶ ἕξει ὁ μὲν ΓΕ ὀδοὺς τὴν τοῦ ΓΗ θέσιν, ὁ δὲ ΕΘ τὴν τοῦ ΓΕ, καὶ πάλιν ὁ ΕΘ θέσιν ἐσχηκὼς τὴν ΓΕ ἐν μιᾶι τοῦ κοχλίου περιστροφῆι ὅλος παραχθήσεται. καὶ ἐπὶ τῶν ἑξῆς ὀδόντων τὰ αὐτὰ ἐπινοεῖν χρή, ὥστε, ὅσους ἂν ὀδόντας ἔχηι τὸ τύμπανον, τοσαυτάκις ὁ κοχλίας κινηθεὶς μίαν ἀποκατάστασιν τοῦ τυμπάνου ποιήσεται.
* * *
[Ex Heronis mechanicis excerpta.] *)
52. λαʹ. Τοσαῦτα μὲν οὖν περὶ τοῦ βαρουλκοῦ, τῶν δὲ προειρημένων εʹ δυνάμεων ἐκ τῶν Ἥρωνος τὴν ἔκθεσιν ἐπιτομώτερον ποιησόμεθα πρὸς ὑπόμνησιν τῶν φιλομαθούντων, προσθέντες ἔτι καὶ τὰ περὶ τῆς μονοκώλου καὶ δικώλου καὶ τρικώλου καὶ τετρακώλου μηχανῆς ἀναγκαίως λεγόμενα, μή ποτε καὶ τῶν βιβλίων ἐν οἷς ταῦτα γέγραπται ἀπορία γένηται τῶι ζητοῦντι· καὶ γὰρ ἡμεῖς κατὰ πολλὰ μέρη διεφθαρμένοις ἐνετύχομεν ἀνάρχοις τε καὶ ἀτελέσι βιβλίοις. πέντε τοίνυν οὐσῶν δυνάμεων δι' ὧν τὸ δοθὲν βάρος τῆι δοθείσηι βίαι κινεῖται, ἀναγκαῖόν ἐστιν τά τε σχήματα αὐτῶν καὶ τὰς χρείας ἔτι δὲ καὶ τὰ ὀνόματα ἐκθέσθαι. ἀποδέδοται δὲ ὑπὸ τοῦ Ἥρωνος καὶ Φίλωνος καὶ διότι αἱ προειρημέναι δυνάμεις εἰς μίαν ἄγονται φύσιν, καίτοι παρὰ πολὺ διαλλάσσουσαι τοῖς σχήμασιν. ὀνόματα μὲν οὖν ἐστιν τάδε· ἄξων ἐν περιτροχίωι, μοχλός, πολύσπαστον, σφήν, καὶ πρὸς τούτοις ὁ καλούμενος ἄπειρος κοχλίας.
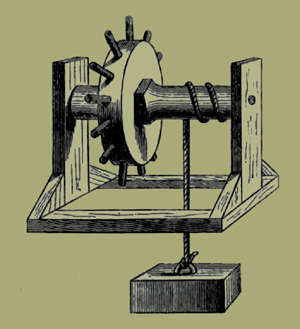
53. Ὁ μὲν οὖν ἄξων ὁ ἐν τῶι περιτροχίωι κατασκευάζεται οὕτως· ξύλον δεῖ λαβεῖν εὔτονον τετράγωνον (καθάπερ δοκίδα) καὶ τούτου τὰ ἄκρα σιμώσαντα στρογγύλα ποιῆσαι καὶ χοινικίδας περιθεῖναι χαλκᾶς συναραρυίας τῶι ἄξονι, ὥστε ἐμβληθείσας αὐτὰς εἰς τρήματα στρογγύλα ἐν ἀκινήτωι τινὶ πήγματι εὐλύτως στρέφεσθαι τῶν τρημάτων τριβεῖς χαλκοῦς ἐχόντων ὑποκειμένους ταῖς χοινικίσι· καλεῖται δὲ τὸ εἰρημένον ξύλον ἄξων. περὶ δὲ μέσον τὸν ἄξονα περιτίθεται τύμπανον ἔχον τρῆμα τετράγωνον ἁρμοστὸν τῶι ἄξονι, ὥστε ἅμα στρέφεσθαι τόν τε ἄξονα καὶ τὸ περιτρόχιον.
Ἡ μὲν οὖν κατασκευὴ δεδήλωται, χρεία δ' ἐστὶν ἡ μέλλουσα λέγεσθαι. ὅταν γὰρ βουλώμεθα μεγάλα βάρη κινεῖν ἐλάσσονι βίαι, τὰ ἐκδεδεμένα ἐκ τοῦ βάρους ὅπλα περιθέντες περὶ τὰ σεσιμωμένα τοῦ ἄξονος, καὶ ἐμβαλόντες σκυτάλας εἰς τὰ ἐν τῶι περιτροχίωι τρήματα, ἐπιστρέφομεν τὸ περιτρόχιον κατάγοντες τὰς σκυτάλας, καὶ οὕτως εὐκόπως κινηθήσεται τὸ βάρος ὑπὸ ἐλάσσονος δυνάμεως τῶν ὅπλων περὶ τὸν ἄξονα ἐπειλουμένων [ἢ καὶ διαμηρυομένων ὑπό τινος πρὸς τὸ μὴ ἅπαν τὸ ὅπλον περικεῖσθαι τῶι ἄξονι]. τοῦ δὲ εἰρημένου ὀργάνου τὸ μὲν μέγεθος ἁρμόζεσθαι δεῖ πρὸς τὰ μέλλοντα κινεῖσθαι βάρη, τὴν δὲ συμμετρίαν πρὸς τὸν λόγον ὃν ἔχει τὸ κινούμενον βάρος πρὸς τὴν κινοῦσαν δύναμιν, ὡς ἑξῆς δειχθήσεται.
54. Ἦν δὲ δευτέρα δύναμις ἡ διὰ τοῦ μοχλοῦ [καὶ τάχα ἡ προεπίνοια τῆς περὶ τὰ ὑπεράγαν βάρη κινήσεως]· προελόμενοι γάρ τινες μεγάλα βάρη κινεῖν, ἐπειδὴ ἀπὸ τῆς γῆς ἔδει πρῶτον μετεωρίσαι, λαβὰς δὲ οὐκ εἶχον διὰ τὸ πάντα τὰ μέρη τῆς ἕδρας τοῦ φορτίου ἐπικεῖσθαι τῶι ἐδάφει, ὑπορύξαντες βραχὺ καὶ ξύλου μακροῦ τὸ ἄκρον ὑποβαλόντες ὑπὸ τὸ φορτίον κατῆγον ἐκ τοῦ ἑτέρου ἄκρου, ὑποθέντες τῶι ξύλωι παρ' αὐτὸ τὸ φορτίον λίθον, ὃ δὴ καλεῖται ὑπομόχλιον. φανείσης δ' αὐτοῖς τῆς κινήσεως πάνυ εὐκόπου ἐνόησαν ὅτι δυνατὸν κινεῖσθαι μεγάλα βάρη διὰ τοῦ τρόπου τούτου. καλεῖται δὲ τὸ ξύλον μοχλός, εἴτε τετράγωνον εἴη εἴτε στρογγύλον. ὅσωι δ' ἂν ἐγγυτέρω τιθῆται τοῦ φορτίου τὸ ὑπομόχλιον, τοσούτωι εὐχερέστερον κινεῖται τὸ βάρος, ὡς ἑξῆς δειχθήσεται.
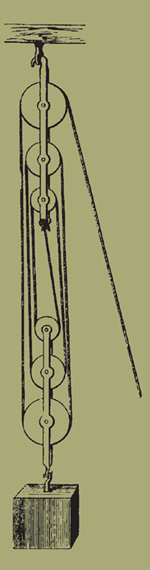
55. Ἔστιν δὲ ἡ τρίτη δύναμις ἡ κατὰ τὸ πολύσπαστον. ὅταν γὰρ βουλώμεθά τι βάρος ἕλκειν, ἐξάψαντες ὅπλον ἐξ αὐτοῦ ἐπισπώμεθα τοσαύτηι βίαι, ὅση τῶι φορτίωι ἰσόρροπός ἐστιν. ἐὰν δὲ ἑλκύσαντες ἐκ τοῦ φορτίου τὸ ὅπλον τὴν μὲν μίαν αὐτοῦ ἀρχὴν ἐκδήσωμεν ἔκ τινος μένοντος χωρίου, τὴν δὲ ἑτέραν βάλωμεν διὰ τροχίλου ἐκδεδεμένου ἐκ τοῦ φορτίου καὶ ταύτην ἐπισπώμεθα, εὐχερέστερον κινήσομεν τὸ βάρος. πάλιν δὲ ἐὰν ἐκ τοῦ μένοντος χωρίου ἐξάψωμεν ἕτερον τροχίλον καὶ τὴν ἀγομένην ἀρχὴν διαβαλόντες διὰ τούτου ἐπισπώμεθα, ἔτι μᾶλλον εὐχερέστερον κινήσομεν τὸ βάρος. καὶ πάλιν ἐὰν ἐκ τοῦ φορτίου τροχίλον ἕτερον ἐκδήσωμεν καὶ τὴν ἀγομένην ἀρχὴν διὰ τούτου διαβαλόντες ἐπισπώμεθα, πολλῶι μᾶλλον εὐχερέστερον κινήσομεν τὸ βάρος <καὶ οὕτως> ἀεὶ τροχίλους ἔκ τε τοῦ μένοντος χωρίου ἐξάπτοντες καὶ ἐκ τοῦ φορτίου καὶ διαβάλλοντες ἐναλλὰξ τὴν ἀγομένην ἀρχὴν εἰς τοὺς τροχίλους εὐχερέστερον κινήσομεν τὸ βάρος. [ὅσωι δ' ἂν εἰς πλείονα κῶλα τὸ ὅπλον κάμπτηται, τὸ βάρος εὐκοπώτερον κινηθήσεται· δεῖ δὲ τὴν ἐκδεννυμένην ἀρχὴν ἐκ τοῦ μένοντος χωρίου ἐξάπτεσθαι.] ἵνα οὖν μὴ καθ' ἕνα τοὺς τροχίλους ἔκ τε τοῦ μένοντος χωρίου καὶ ἐκ τοῦ φορτίου ἐξάπτωμεν, οἱ μὲν εἰρημένοι εἰς τὸ μένον εἶναι χωρίον εἰς ἓν ξύλον ἐντίθενται περὶ ἄξονας κινούμενοι, ὃ καλεῖται μάγγανον, τοῦτο δὲ ἐξάπτεται ἐκ τοῦ μένοντος χωρίου διά τινος ἑτέρου ὅπλου, οἱ δὲ πρὸς τῶι φορτίωι εἰς ἕτερον μάγγανον τούτωι ἴσον, ὃ δὴ πάλιν ἐξάπτεται ἐκ τοῦ φορτίου μόνον. οὕτως δὲ δεῖ κατατετάχθαι ἐν τοῖς μαγγάνοις τοὺς τροχίλους, ὥστε τὰ κῶλα μὴ ἐμπλεκόμενα πρὸς ἄλληλα δυσπειθῆ γίνεσθαι. δι' ἣν δ' αἰτίαν πλειόνων τῶν κώλων γινομένων εὐκοπία παρακολουθεῖ, δείξομεν, καὶ δι' ἣν αἰτίαν ἡ ἑτέρα ἀρχὴ ἐκ τοῦ μένοντος ἐξάπτεται χωρίου.
56. Ἡ δὲ ἑξῆς δύναμις ἡ διὰ τοῦ σφηνὸς καὶ αὐτὴ μεγάλας χρείας παρεχομένη πρός τε τὰς μυρεψικὰς πιέσεις καὶ τὰς διὰ τῆς τεκτονικῆς ὑπεραγούσας κολλήσεις, τὸ δὲ πάντων μέγιστον, ὅταν τοὺς ἐκ τῶν λατομιῶν λίθους ἀποσπᾶν δέηι τῆς κατὰ τὸ κάτω μέρος συνεχείας, οὐδεμία τῶν ἄλλων δυνάμεων ἐνεργεῖν δύναται, οὐδ' ἂν ἅμα πᾶσαι συζευχθῶσιν, μόνος δὲ ὁ σφὴν ἐνεργεῖ διὰ τῆς τυχούσης, καὶ ἄνεσις μὲν οὐδ' ἡτισοῦν γίνεται κατὰ τὰ διαλήμματα τῶν ἐργαζομένων, καρτερὰ δὲ ἡ ἐπίτασις. τοῦτο δὲ φανερὸν ἐκ τοῦ καὶ μὴ πλησσομένου τοῦ σφηνὸς ἐνίοτε ψόφους καὶ ῥήγματα γίνεσθαι διὰ τῆς τοῦ σφηνὸς ἐνεργείας. ὅσωι δ' ἂν ἡ τοῦ σφηνὸς γωνία ἐλάσσων γίνηται, τοσούτωι εὐχερέστερον ἐνεργεῖ, τουτέστιν δι' ἐλάσσονος πληγῆς, ὡς δείξομεν.
57. Τὰ μὲν οὖν προειρημένα ὄργανα φανερὰς καὶ αὐτοτελεῖς ἔχει τὰς κατασκευὰς πολλαχοῦ ἐν ταῖς χρείαις φαινομένας, ὁ δὲ κοχλίας ἔχει τι περίεργον περί τε τὴν κατασκευὴν καὶ τὴν χρῆσιν. ὁτὲ μὲν [οὖν] γὰρ αὐτὸς καθ' αὑτὸν μόνος ἐνεργεῖ, ὁτὲ δὲ καὶ προσλαμβάνων ἔτι δύναμιν, πλὴν ὅτι οὐδὲν ἕτερόν ἐστιν ἢ σφὴν εἰλημένος, ἀπολειπόμενος τῆς πληγῆς, διὰ μοχλοῦ δὲ καὶ στροφῆς τὴν κίνησιν ποιούμενος. τοῦτο δ' ἔσται δῆλον ἐκ τῶν μελλόντων λέγεσθαι. φύσις μὲν οὖν ὑπάρχει τῆς περὶ αὐτὸν πραγματείας τοιαύτη· ἐὰν κυλίνδρου πλευρὰ φέρηται κατὰ τῆς τοῦ κυλίνδρου ἐπιφανείας, πρὸς δὲ τῶι πέρατι ταύτης σημεῖόν τι ἅμα κατὰ αὐτῆς τῆς πλευρᾶς φέρηται, καὶ ἐν τῶι αὐτῶι χρόνωι ἥ τε πλευρὰ μίαν ἀποκατάστασιν ποιήσηται καὶ τὸ σημεῖον τὸ πᾶν τῆς πλευρᾶς διεξέλθηι, ἡ γενομένη ὑπὸ τοῦ σημείου ἐν τῆι κυλινδρικῆι ἐπιφανείαι γραμμὴ ἕλιξ ἐστίν, ἣν δὴ κοχλίαν καλοῦσιν. καταγράφεται δὲ ἐν τῶι κυλίνδρωι οὕτως· ἐὰν ἐν ἐπιπέδωι δύο εὐθείας ἐκθώμεθα ὀρθὰς ἀλλήλαις, ὧν ἡ μὲν μία ἴση ἐστὶν τῆι τοῦ εἰρημένου κυλίνδρου πλευρᾶι, ἡ δὲ ἑτέρα τῆι τοῦ κύκλου περιφερείαι, ὅς ἐστιν βάσις τοῦ κυλίνδρου, καὶ ἐπὶ τὰ πέρατα τῶν εἰρημένων εὐθειῶν ἐπιζεύξωμεν εὐθεῖαν ὑποτείνουσαν τὴν ὀρθὴν γωνίαν, τεθῆι δὲ ἡ ἴση τῆι τοῦ κυλίνδρου πλευρᾶι ἐπὶ τὴν τοῦ κυλίνδρου πλευράν, ἡ δὲ ἑτέρα τῶν περὶ τὴν ὀρθὴν ἐπειληθῆι κατὰ τῆς τοῦ κύκλου περιφερείας, εἰληθήσεται καὶ ἡ ὑποτείνουσα τὴν ὀρθὴν κατὰ τῆς κυλινδρικῆς ἐπιφανείας, καθ' ἧς ἔσται ἡ εἰρημένη ἕλιξ. ἔξεστιν δὲ διελόντα τὴν τοῦ κυλίνδρου πλευρὰν εἰς ἴσα, ὁπόσ' ἄν τις προαιρῆται, καθ' ἕκαστον αὐτῆς μέρος περιγράφειν ἕλικα, ὡς προείρηται [ὥστε ἐν τῶι κυλίνδρωι πλείονας ἕλικας γράφεσθαι, καλείσθω δὲ ἡ ἅπαξ εἰληθεῖσα ἕλιξ μονόστροφος, τουτέστιν ἡ περὶ τὰ παρὰ ἑκάστου μέρους γινομένη γραμμή]. 58. κατὰ αὐτῆς οὖν τῆς γραμμῆς σωλῆνα ἐντεμόντες εἰς τὸ βάθος τοῦ κυλίνδρου καὶ ἐκκόψαντες, ὥστε ἐν τῶι σωλῆνι τύλον
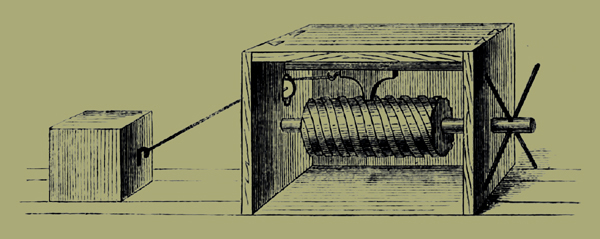
ἐναρμόσαι στερεόν, χρῶνται τῶι κοχλίαι οὕτως· τὰ ἄκρα αὐτοῦ στρογγύλα ποιήσαντες ἐναρμόζουσιν εἴς τινα διαπήγματα ἐν στρογγύλοις τρήμασιν, ὥστε εὐκόπως αὐτὸν στρέφεσθαι, ὑπὲρ δὲ τὸν κοχλίαν κανόνα διατιθέντες παράλληλον αὐτῶι σωλῆνα ἔχοντα μέσον ἐν τῆι ἄνω ἐπιφανείαι ἐναρμόζουσιν εἰς τοῦτον τὸν σωλῆνα τὸν εἰρημένον τύλον, ὥστε τὸ μὲν ἕτερον ἄκρον τοῦ τύλου μένειν ἐν τῶι τοῦ κοχλίου σωλῆνι, τὸ δὲ ἕτερον ἐν τῶι εἰρημένωι ἐτέρωι σωλῆνι τῶι ἐν τῶι κανόνι. ὅταν οὖν βούλωνται φορτίον κινεῖν διὰ τούτου τοῦ ὀργάνου, ὅπλον λαβόντες τούτου τὴν μὲν μίαν ἀρχὴν ἐξάπτουσιν ἐκ τοῦ φορτίου, τὴν δὲ ἑτέραν ἐκ τοῦ προειρημένου τύλου, καὶ τρημάτων ὄντων τῆι κεφαλῆι τοῦ κοχλίου σκυτάλας ἐμβαλόντες κατάγουσιν, καὶ οὕτως ὑπὸ τῆς ἕλικος ὁ τύλος παραγόμενος ἐν τῶι σωλῆνι ἐπισπᾶται τὸ ὅπλον δι' οὗ καὶ τὸ φορτίον. ἔξεστιν δὲ ἀντὶ τῶν σκυταλῶν χειρολάβην τινὰ περιθεῖναι τῶι ἄκρωι τοῦ κοχλίου ὑπερέχοντι εἰς τὸ ἐκτὸς τοῦ διαπήγματος καὶ οὕτως στρέφοντα τὸν κοχλίαν ἐπισπᾶσθαι τὸ φορτίον. ἡ δ' ἐν τῶι κοχλίαι ἕλιξ ὁτὲ μὲν τετράγωνος γίνεται ὁτὲ δὲ φακοειδής, τετράγωνος μέν, ὅταν ὁ ἐν αὐτῶι σωλὴν ὀρθὰς ἔχηι τὰς ἐντομάς, φακοειδὴς δέ, ὅταν λοξὰς καὶ εἰς μίαν συναγομένας γραμμήν. καλεῖται δὲ ὁ μὲν τετράγωνος, ὁ δὲ φακωτός.
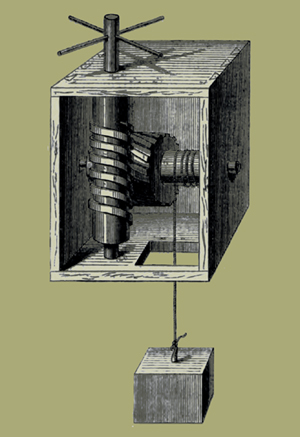
59. Ὅταν μὲν οὖν αὐτὸς καθ' αὐτὸν ὁ κοχλίας ἐνεργῆι, ταύτην λαμβάνει τὴν κατασκευήν, γίνεται δὲ καὶ ἑτέρως· προσλαβόντες γάρ τινα ἑτέραν δύναμιν τὴν διὰ τοῦ ἄξονος τοῦ ἐν τῶι περιτροχίωι καλουμένου [κατασκευὴν] νοήσομεν τὸ περὶ τὸν ἄξονα τύμπανον ὠδοντωμένον εἶναι, κοχλίαν δέ τινα παρακεῖσθαι τῶι τυμπάνωι ἤτοι ὀρθὸν κείμενον πρὸς τὸ ἔδαφος ἢ παράλληλον τῶι ἐδάφει, ἔχοντα τὴν μὲν ἕλικα ἐμπεπλεγμένην τοῖς ὀδοῦσι τοῦ τυμπάνου τὰ δὲ ἄκρα ἐν στρογγύλοις τρήμασιν πολευόμενα ἔν τισιν διαπήγμασιν, καθάπερ καὶ προείρηται, καὶ ὑπεροχῆς οὔσης τοῦ ἄκρου τοῦ κοχλίου εἰς τὸ ἐκτὸς τοῦ διαπήγματος μέρος, ἤτοι χειρολάβην τινὰ περικεῖσθαι, δι' ἧς ἐπιστραφήσεται ὁ κοχλίας, ἢ τρήματα, ὥστε σκυταλῶν ἐμβληθεισῶν ὁμοίως ἐπιστρέφεσθαι· αὐτόν. πάλιν οὖν τὰ ἐκ τοῦ φορτίου ὅπλα περιβαλόντες περὶ τὸν ἄξονα ἐφ' ἑκάτερα τοῦ τυμπάνου καὶ ἐπιστρέφοντες τὸν κοχλίαν, δι' οὗ καὶ τὸ ὠδοντωμένον τύμπανον, ἐπισπασόμεθα τὸ βάρος.
60. Αἱ μὲν οὖν κατασκευαὶ καὶ αἱ χρήσεις τῶν προειρημένων πέντε δυνάμεων δεδήλωνται, τίς δέ ἐστιν ἡ αἰτία, δι' ἣν δι' ἑκάστης αὐτῶν μεγάλα βάρη κινεῖται μικρᾶι παντάπασι δυνάμει, Ἥρων ἀπέδειξεν ἐν τοῖς μηχανικοῖς. ἐν δὲ τοῖς ἑξῆς ἐκ τοῦ γʹ τῶν Ἥρωνος μηχανὰς γράψομεν πρὸς εὐκοπίαν καὶ λυσιτέλειαν ἁρμοζούσας, δι' ὧν πάλιν μεγάλα βάρη κινηθήσεται.
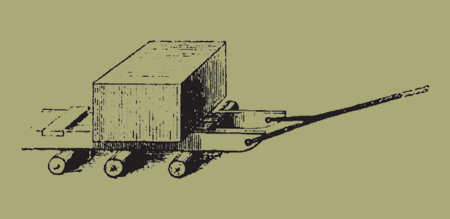
Τὰ μὲν οὖν ἀγόμενα ἐπὶ τοῦ ἐδάφους, φησίν, ἐπὶ χελώνας ἄγεται. ἡ δὲ χελώνη πῆγμά ἐστιν ἐκ τετραγώνων ξύλων συμπεπηγός, ὧν τὰ ἄκρα ἀνασεσίμωται. τούτοις οὖν ἐπιτίθεται τὰ βάρη, καὶ ἐκ τῶν ἄκρων αὐτῶν ἤτοι πολύσπαστα ἐκδέννυται ἢ ὅπλων ἀρχαί. ταῦτα δὲ ἤτοι ἀπὸ χειρὸς ἕλκεται ἢ εἰς ἐργάτας ἀποδίδοται, ὧν περιαγομένων ἡ χελώνη ἐπὶ τοῦ ἐδάφους σύρεται ὑποβαλλομένων σκυταλίων ἢ σανίδων. ἐὰν μὲν γὰρ μικρὸν ἦι τὸ φορτίον, σκυτάλαις χρῆσθαι δεῖ, ἐὰν δὲ μεῖζον, ταῖς σανίσιν διὰ τὸ ταύτας μὴ εὐκόλως σύρεσθαι· αἱ γὰρ σκυτάλαι κυλιόμεναι κίνδυνον ἔχουσιν τοῦ φορτίου ὁρμὴν λαβόντος. ἔνιοι δὲ οὔτε σκυτάλαις οὔτε σανίσι χρῶνται, ἀλλὰ τροχοὺς ναστοὺς προσθέντες ταῖς χελώναις ἄγουσιν.
61. λβʹ. Ἐπὶ δὲ τῶν εἰς ὕψος βασταζομένων φορτίων, φησίν, μηχαναὶ γίνονται αἱ μὲν μονόκωλοι, αἱ δὲ δίκωλοι, αἱ δὲ τρίκωλοι, αἱ δὲ τετράκωλοι. αἱ μὲν οὖν μονόκωλοι οὕτως· ξύλον εὔτονον λαμβάνεται ὕψος ἔχον μεῖζον ἢ οὗ βουλόμεθα τὸ φορτίον μετεωρίσαι, κἂν μὲν αὐτὸ καθ' αὑτὸ ἰσχυρὸν ἦι, ὅπλον βάλλοντες περὶ αὐτὸ [καὶ σφίγγοντες] καὶ διαμηρυόμενοι κατὰ ἐπείλησιν ἀποσφίγγουσιν. τῶν δὲ ἐπειλήσεων τὸ μεταξὺ διάστημα οὐ πλεῖον γίνεται παλαιστῶν δʹ, καὶ οὕτως εὐτονώτερόν τε γίνεται τὸ ξύλον καὶ αἱ τοῦ ὅπλου ἐπειλήσεις ὥσπερ βαθμοὶ τοῖς ἐργαζομένοις καὶ βουλομένοις εἰς τὸ ἄνω μετεωρίζεσθαι εὔχρηστοι γίνονται. ἐὰν δὲ μὴ ἦι εὔτονον τὸ ξύλον, ἐκ πλειόνων συμβλητὸν γίνεται. [στοχάζεσθαι δεῖ τῶν μελλόντων βαστάζεσθαι φορτίων, ὅπως μὴ ἀσθενέστερον τὸ κῶλον ὑπάρχηι.] ἵσταται οὖν τὸ κῶλον ὀρθὸν ἐπί τινος ξύλου καὶ ἐκ τοῦ ἄκρου αὐτοῦ ὅπλα ἐκδέννυται τρία που ἢ τέσσαρα καὶ ἀποτεθέντα ἀποδίδοται πρός τινα μένοντα χωρία, ὅπως τὸ ξύλον, ὅπου ἄν τις βιάζηται, μὴ παραχωρῆι κατεχόμενον ὑπὸ τῶν ἀποτεταμένων ὅπλων. ἐκ δὲ τοῦ ἄνω μέρους αὐτοῦ πολύσπαστα ἐξάψαντες καὶ ἀποδιδόντες εἰς τὸ φορτίον ἐπισπῶνται ἤτοι ἀπὸ χειρὸς ἢ εἰς ἐργάτας ἀποδόντες, εἰς ὅταν μετεωρισθῆι τὸ φορτίον. κἂν δέηι τὸν λίθον ἐκτεθῆναι ἐπὶ τεῖχος ἢ ὅπου βούλεταί τις, ἐκλύσαντες ἓν τῶν ἐκδεννυμένων ἐκ τοῦ ἄκρου ὅπλων τὸ ἐπὶ τὰ ἕτερα μέρη τοῦ φορτίου κείμενον ἐγκλίνουσιν τὸ κῶλον, ἢ τὰς σκυτάλας ὑποβάλλοντες ὑπὸ τὸ φορτίον ἐν τοῖς μέρεσιν, ἐν οἷς ἡ σφενδόνη ἐν τῶι λίθωι οὐκ ἐπείληται, χαλῶσι τὰ ἀγόμενα τῶν πολυσπάστων ἄχρι ἂν ἐπικαθίσηι τὸ φορτίον ταῖς σκυτάλαις, εἶτ' ἐκλύσαντες τὴν σφενδόνην μοχλεύουσι τὸ φορτίον ἄχρι οὗ εἰς ὃν βούλονται τόπον παράξωσιν. εἶτα πάλιν τὸ ὑποκείμενον τῶι κώλωι ξύλον ὅπλωι ἐπισπασάμενοι ἀπὸ χειρὸς περιάγουσιν ἐπὶ ἕτερον μέρος τοῦ οἰκοδομήματος ἅμα ἀνιέντες τοὺς ἀποτόμους, καὶ πάλιν ἐκδήσαντες χρῶνται, ὡς προείρηται.
* * *
――――――
*) Τοσαῦτα et cetera usque ad exitum libri alius quidam scriptor (idem fortasse atque ille de quo p. 1022, 13 dictum est) ad Pappi collectionem sub finem mutilatam addidisse videtur.
|




















