| |
ιβʹ
Ἀποδεδειγμένων νῦν τούτων ἔσται δεῖξαι ὅτι, ἐάν παράλληλοι ὦσιν αἱ ΑΒ ΓΔ, καὶ εἰς αὐτὰς ἐμπίπτωσιν εὐθεῖαί τινες αἱ ΑΔ ΑΖ ΒΓ ΒΖ, καὶ ἐπιζευχθῶσιν αἱ ΕΔ ΕΓ, [ὅτι] γίνεται εὐθεῖα ἡ διὰ τῶν Η Μ Κ.
Ἐπεὶ γὰρ τρίγωνον τὸ ΔΑΖ, καὶ τῆι ΔΖ παράλληλος ἡ ΑΕ, καὶ διῆκται ἡ ΕΓ συμπίπτουσα τῆι ΔΖ κατὰ τὸ Γ, διὰ τὸ προγεγραμμένον γίνεται ὡς ἡ ΔΖ πρὸς τὴν ΖΓ, οὕτως τὸ ὑπὸ ΓΕ ΗΘ πρός τὸ ὐπὸ ΓΗ ΘΕ. πάλιν ἐπεὶ τρίγωνόν ἐστιν τὸ ΓΒΖ, καὶ τῆι ΓΔ παράλληλος ἦκται ἡ ΒΕ, καὶ διῆκται ἡ ΔΕ συμπίπτουσα τῆι ΓΖΔ κατὰ τὸ Δ, γίνεται ὡς ἡ ΓΖ πρὸς τὴν ΖΔ, οὕτως τὸ ὑπὸ ΔΕ ΛΚ πρὸς τὸ ὑπὸ ΔΚ ΛΕ· ἀνάπαλιν ἄρα γίνεται ὡς ἡ ΔΖ πρὸς τὴν ΖΓ, οὕτως τὸ ὑπὸ ΔΚ ΛΕ πρὸς τὸ ὑπὸ ΔΕ ΛΚ. ἦν δὲ καὶ ὡς ἡ ΔΖ, πρὸς τὴν ΖΓ, οὕτως τὸ ὑπὸ ΓΕ ΗΘ πρὸς τὸ ὑπὸ ΓΗ ΘΕ· καὶ ὡς ἄρα τὸ ὑπὸ ΓΕ ΗΘ πρὸς τὸ ὑπὸ ΓΗ ΘΕ, οὕτως ἐστὶν τὸ ὑπὸ ΔΚ ΛΕ πρὸς τὸ ὑπὸ ΔΕ ΚΛ [ἀνῆκται εἰς τὸ πρὸ ἑνός], ἐπεὶ οὖν εἰς δύο εὐθείας τὰς ΓΜΛ ΔΜΘ δύο εὐθεῖαι διηγμέναι εἰσὶν αἱ ΕΓ ΕΔ, καὶ ἔστιν ὡς τὸ ὑπὸ ΓΕ ΗΘ πρὸς τὸ ὑπὸ ΓΗ ΘΕ, οὕτως τὸ ὑπὸ ΔΚ ΕΛ πρὸς τὸ ὑπὸ ΔΕ ΛΚ, εὐθεῖα ἄρα ἐστὶν ἡ διὰ τῶν Η Μ Κ· τοῦτο γὰρ προδέδεικται.
ιγʹ
Ἀλλα δὴ μὴ ἔστωσαν αἱ ΑΒ ΓΔ παράλληλοι, ἀλλὰ συμπιπτέτωσαν κατὰ τὸ Ν· ὅτι πάλιν εὐθεῖά ἐστιν ἡ διὰ τῶν Η Μ Κ.
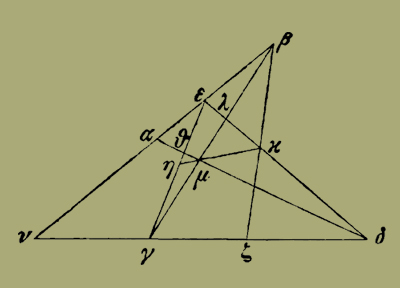
Ἐπεὶ εἰς τρεῖς εὐθείας τὰς ΑΝ ΑΖ ΑΔ ἀπὸ τοῦ αὐτοῦ σημείου τοῦ Γ δύο διηγμέναι εἰσὶν αἱ ΓΕ ΓΔ, γίνεται ὡς τὸ ὑπὸ ΓΕ ΗΘ πρὸς τὸ ὑπὸ ΓΗ ΘΕ, οὕτως τὸ ὑπὸ τῶν ΓΝ ΖΔ πρὸς τὸ ὑπὸ τῶν ΝΔ ΓΖ. πάλιν ἐπεὶ ἀπὸ τοῦ αὐτοῦ σημείου τοῦ Δ εἰς τρεῖς εὐθείας τὰς ΒΝ ΒΓ ΒΖ δύο εἰσὶν διηγμέναι αἱ ΔΕ ΔΝ, ἔστιν ὡς τὸ ὑπὸ ΝΓ ΖΔ πρὸς τὸ ὑπὸ ΝΔ ΖΓ, οὕτως τὸ ὑπὸ ΔΚ ΕΛ πρὸς τὸ ὑπὸ ΔΕ ΚΛ. ἀλλ' ὡς τὸ ὑπὸ ΝΓ ΖΔ πρὸς τὸ ὑπὸ ΝΔ ΓΖ, οὕτως ἐδείχθη τὸ ὑπὸ ΓΕ ΗΘ πρὸς τὸ ὑπὸ ΓΗ ΘΕ· καὶ ὡς ἄρα τὸ ὑπὸ ΓΕ ΘΗ πρὸς τὸ ὑπὸ ΓΗ ΘΕ, οὕτως ἐστὶν τὸ ὑπὸ ΔΚ ΕΛ πρὸς τὸ ὑπὸ ΔΕ ΚΛ [ἀπῆκται εἰς ὃ καὶ ἐπὶ τῶν παραλλήλων]. διὰ δὴ τὸ προγεγραμμένον εὐθεῖά ἐστιν ἡ διὰ τῶν Η Μ Κ.
――――――
XII. Propositio 138
Iam his demonstratis ostendendum erit, si parallelae sint αβ γδ, et in eas incidant quaedam rectae αδ αζ βγ βζ, quarum αδ βγ concurrant in μ *), et a quovis rectae αβ puncto inter α et β sumpto ducantur εγ εδ, quarum εγ cum αζ concurrat in η et εδ cum βζ in κ, rectam esse quae per η μ κ transit.
Quoniam enim triangulum est δαζ, et rectae δζ parallela αε et ducta est εγ cum δζ producta concurrens in γ, propter superius lemma XI fit δζ : ζγ = γε · ηθ : γη · θε. Rursus quia est triangulum γβζ, et rectae γζ parallela εβ, et ducta est εδ cum recta γζδ concurrens in δ, fit γζ : ζδ = δε · κλ : δκ · λε. E contrario igitur est
δζ : ζγ = δκ · λε : δε · κλ. Sed erat etiam
δζ : ζγ = γε · ηθ : γη · θε; ergo etiam
γε · ηθ : γη · θε = δκ · λε : δε · κλ.
Iam quia in duas rectas γμλ δμθ duae rectae εγ εδ ductae sunt, estque γε · ηθ : γη · θε = δκ · λε : δε · κλ, recta igitur est quae per η μ κ transit; hoc enim supra lemmate X demonstratum est.
XIII. Propositio 139
At ne sint parallelae αβ γδ, sed convergant in puncto ν; dico rursus rectam esse quae per η μ κ transit.
Quoniam in tres rectas αν αζ αδ ab eodem puncto γ duae rectae γε γδ ductae sunt, propter superius lemma III fit γε · ηθ : γν · θε = γν · ζδ : νδ · γζ. Rursus quia ab eodem puncto δ in tres rectas βν βγ βζ duae ductae sunt δε δν, propter idem lemma est
νγ · ζδ : νδ · ζγ = δκ · ελ : δε · κλ. Sed demonstratum est
νγ · ζδ : νδ · ζγ = γε · ηθ : γη · θε; ergo etiam
γε · ηθ : γη · θε = δκ · ελ : δε · κλ.
Igitur propter superius lemma X recta est quae per η μ κ transit.
――――――
*) Haec addita secundum Simsonum, reliqua a nobis; praeterea totam propositionem alia eaque explicatiore ratione enuntiat Simsonus.
|
