|
Κεφ. κδʹ.
Μέθοδος εἰς τὴν ἐν ἐπιπέδωι τῆς οἰκουμένης
σύμμετρον τῆι σφαιρικῆι θέσει καταγραφήν.
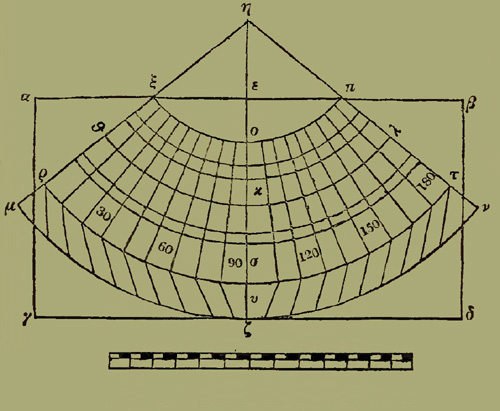
§ 1. Ἐπὶ δὲ τῆς ἐν τῶι πίνακι καταγραφῆς ἡ τῆς συμμετρίας τῶν ἄκρων παραλλήλων μέθοδος ἡμῖν ἔσται τοιαύτη. Κατασκευάσομεν πίνακα παραλληλόγραμμον ὀρθογώνιον, οἷός ἐστιν ὁ αβγδ, διπλασίαν ἔχοντα {48} ἔγγιστα τὴν αβ πλευρὰν τῆς αγ· ὑποκείσθω δὲ ἡ αβ κατὰ τὴν ἄνω θέσιν, ἐσομένη ἐπὶ τὰ βόρεια μέρη τῆς καταγραφῆς· § 2. ἔπειτα διελόντες τὴν αβ δίχα τε καὶ πρὸς ὀρθὰς τῆι εζ εὐθείαι προσαρμόσομεν αὐτῆι κανόνα σύμμετρον καὶ ὀρθὸν· ὥστε τὴν ἐπὶ τοῦ μήκους αὐτοῦ μέσην γραμμὴν ἐπὶ μιᾶς εὐθείας συνίστασθαι τῆι εζ, ὡς τὴν περὶ τὴν εη· καὶ γινέσθω ἡ εη τοιούτων λδʹ, οἵων ἐστὶν ἡ ηζ εὐθεῖα, ρλαʹ γʹ ιβʹ· κέντρωι τῶι η, καὶ διαστήματι, τῶι ἀπέχοντι αὐτοῦ σημείωι, ἐπὶ τῆς ηζ τμήματα οθʹ κύκλον γράψομεν τὸν ἐσόμενον ἀντὶ τοῦ διὰ Ῥόδου παραλλήλου, ὡς τὸν θκλ. § 3. Πρὸς μὲν δὴ τοὺς τοῦ μήκους {49} ὅρους, ἓξ ὡριαίων διαστημάτων συναγομένους ἐφ᾽ ἑκάτερα τοῦ κ λαβόντες τὴν ἐπὶ τῆς ηζ τοῦ μέσου μεσημβρινοῦ γραμμῆς διάστασιν τεσσάρων διαστημάτων, ἐπὶ τοῦ διὰ τῆς Ῥοδίας παραλλήλου πέντε ὁμοίων, διὰ τὸν ἐπιτέταρτον ἔγγιστα λόγον τοῦ μεγίστου κύκλου πρὸς αὐτόν, καὶ τηλικαύτας ὀκτωκαίδεκα διεκβαλόντες ἐφ᾽ ἑκάτερα τοῦ κ κατὰ τὴν θκλ περιφέρειαν, ἕξομεν τὰ σημεῖα, δι᾽ ὧν ἐπιζευγνύναι δεήσει ἀπὸ τοῦ η, τοὺς τὰ τριτημόρια ια τῶν ὡρῶν διαστήματα περιέξοντας μεσημβρινοὺς, ὥστε καὶ τοὺς ἀφορίζοντας τὰ πέρατα τόν τε ηθμ καὶ τὸν ηλν. § 4. Γραφήσεται δὲ ἀκολούθως καὶ ὁ μὲν διὰ Θούλης διαστήματι τῶι ἀπέχοντι ἀπὸ τοῦ η ἐπὶ τῆς ζη τμήματα νβʹ, ὡς ὁ ξοπ· ὁ δὲ ἰσημερινὸς τῶι ἀπέχοντι τοῦ η ὁμοίως τμήματα ριεʹ, ὡς ὁ ρστ, ὁ δὲ ἀντικείμενος τῶι διὰ Μερόης καὶ νοτιώτατος, τῶι ἀπέχοντι τοῦ η τμήματα ρλαʹ γʹ ιβʹ, ὡς ὁ μυν. § 5. Συναχθήσεται οὖν ὁ μὲν τῆς ρστ πρὸς τὴν ξοπ λόγος ὁ τῶν ριεʹ πρὸς τὰ νβʹ κατὰ τὸν ἐπὶ τῆς σφαίρας τῶν παραλλήλων τούτων λόγον. § 6. Ἐπειδὴ καὶ οἵων μὲν ἡ ησ ὑπόκειται ριεʹ, τοιούτων ἐστὶ καὶ ἡ ηο τμημάτων νβʹ, ὡς δὲ ἡ ησ πρὸς τὴν ηο, οὕτως ἡ ρστ περιφέρεια πρὸς τὴν ξοπ. Καταληφθήσεται δὲ καὶ ἡ μὲν οκ τοῦ μεσημβρινοῦ διάστασις, τουτέστιν ἡ ἀπὸ τοῦ διὰ Θούλης ἐπὶ τὸν διὰ Ῥόδου τμημάτων κζʹ· ἡ δὲ κσ, τουτέστιν ἡ ἀπὸ τοῦ Ῥόδου μέχρι τοῦ ἰσημερινοῦ τῶν αὐτῶν λςʹ· ἡ δὲ σλυ, τουτέστιν ἡ ἀπὸ τοῦ ἰσημερινοῦ ἐπὶ τὸν ἀντικείμενον τῶι διὰ Μερόης τῶν αὐτῶν ιςʹ γʹ ιβʹ· καὶ ἔτι οἵων ἐστὶν ἡ ου κατὰ πλάτος τῆς ἐγνωσμένης γῆς διάστασις οθʹ γʹ ιβʹ ἢ ὅλων πʹ, τοιούτων ἔσται καὶ ἡ θκλ μέση {50} κατὰ μῆκος διάστασις, ρμδʹ, ἀκολούθως τοῖς ἐκ τῶν ἀποδείξεων ὑποτιθεμένοις· τὸν αὐτὸν γὰρ τούτωι λόγον ἔχουσιν ἔγγιστα καὶ οἱ τετρακισμύριοι τοῦ πλάτους στάδιοι πρὸς τοὺς ἑπτακισμυρίους καὶ δισχιλίους τοῦ κατὰ τὸν διὰ τῆς Ῥοδίας παράλληλον μήκους· καὶ τοὺς λοιποὺς δὲ τῶν παραλλήλων γράψομεν, ἐὰν προαιρώμεθα κέντρωι πάλιν τῶι η καὶ διαστήμασι τοῖς ἀπέχουσιν ἀπὸ τοῦ σ τὰ ἴσα τμήματα τοῖς ἐκκειμένοις ἐπὶ τῶν ἀποχῶν τοῦ ἰσημερινοῦ. § 7. Ἐξέσται δ᾽ ἡμῖν καὶ μὴ διευθύνειν τὰς ἀντὶ τῶν μεσημβρινῶν γραμμὰς ἕως τοῦ μυν παραλλήλου, ἀλλὰ μέχρι μόνου τοῦ ρστ ἰσημερινοῦ· ἔπειτα διελοῦσι τὴν μυν περιφέρειαν εἰς [ἐνενήκον] ἴσα τε καὶ ἰσάριθμα τμήματα τοῖς ἐπὶ τοῦ διὰ Μερόης εἰλημμένοις ἐπὶ αὐτὰς τὰς τομὰς ἐπιζευγνύειν ἀπὸ τῶν κατὰ τὸν ἰσημερινὸν τὰς μεταξὺ πιπτούσας εὐθείας τῶν μεσημβρινῶν, ὅπως ἐμφαίνηταί πως ἡ ἐπὶ θάτερα τοῦ ἰσημερινοῦ πρὸς μεσημβρίαν ἀποκλίνουσα θέσις ἐκ τῆς μεταλαμβανομένης ἐπιστροφῆς, ὡς ἔχουσιν αἱ ρφ καὶ τχ γραμμαί.
§ 8. Λοιπὸν δὲ ἕνεκεν τοῦ προχείρου τῆς τῶν κατατασσομένων τόπων παρασημειώσεως ποιήσομεν πάλιν κανόνιον στενὸν, ἴσον τῶι μήκει τῆι ηζ ἢ τῆι ησ μόνηι, καὶ ἐμπολίσαντες αὐτὸ περὶ τὸ η, ὥστε παραφερομένου καθ᾽ ὅλον τὸ μῆκος τῆς καταγραφῆς ἐφαρμόζειν ἀκριβῶς τὴν ἑτέραν τῶν πλευρῶν ταῖς τῶν μεσημβρινῶν εὐθείαις, διὰ τὸ κατὰ μέσου τοῦ πόλου τὴν ἐκτομὴν αὐτῆς πίπτειν, διελοῦμεν ταύτην τὴν πλευρὰν εἰς τὰ ἐπιβάλλοντα ἤτοι τῆι ηζ τμήματα ρλαʹ γʹ ιβʹ, ἢ τῆι ησ μόνηι τμήματα ριεʹ, καὶ παρασημειωσόμεθα τοὺς ἀριθμοὺς ἀπὸ τῆς κατὰ τὸν ἰσημερινὸν τομῆς {51} ποιούμενοι τὴν ἀρχὴν, ἀφ᾽ ὧν καὶ τοὺς παραλλήλους ἐξέσται γράφειν, ἵνα μὴ τὸν ἐπὶ τῆς καταγραφῆς μεσημβρινὸν εἰς πάντα τὰ τμήματα διαιροῦντες καὶ παρασημειούμενοι συγχέωμεν τὰς ἐσομένας πρὸς αὐτῶι τῶν τόπων ἐπιγραφάς. § 9. Διελόντες οὖν καὶ τὸν ἰσημερινὸν εἰς τὰς τῶν δώδεκα ὡρῶν ρπ° μοίρας, καὶ παραθέντες τοὺς ἀριθμοὺς ἀπὸ τῆς κατὰ τὸν δυσμικώτατον μεσημβρινὸν ἀρχῆς, παροίσομεν ἀεὶ τὴν τοῦ κανονίου πλευρὰν ἐπὶ τὴν δηλουμένην τοῦ μήκους μοῖραν· καὶ διὰ τῆς ἐν τῶι κανονίωι διαιρέσεως ἐπὶ τὴν κατὰ πλάτος σημαινομένην θέσιν ἀφικνούμενοι, τὴν δέουσαν ἐφ᾽ ἑκάστου ποιησόμεθα σημείωσιν, τὸν αὐτὸν τρόπον τοῖς ἐπὶ τῆι σφαίραι ὑποδεδειγμένοις.
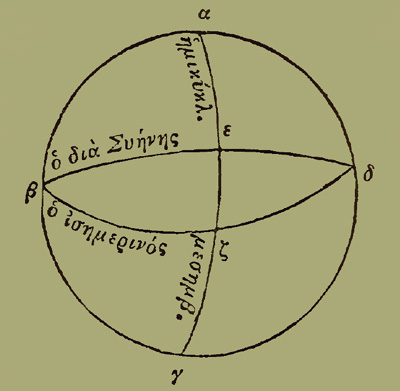
§ 10. Ἔτι δ᾽ ἂν ὁμοιότερόν τε καὶ συμμετρώτερον ποιοίμεθα τὴν ἐν τῶι πίνακι τῆς οἰκουμένης καταγραφὴν, εἰ καὶ τὰς μεσημβρινὰς γραμμὰς καταλάβοιμεν τῆι φαντασίαι τῶν ἐπὶ τῆς σφαίρας μεσημβρινῶν γραμμῶν· {52} ὡς τοῦ ἄξονος τῶν ὄψεων διήκοντος ἐν τῆι θέσει τῆς σφαίρας, διά τε τῆς πρὸς τῆι ὄψει τομῆς, τοῦ διχοτομοῦντος τὸ μῆκος τῆς ἐγνωσμένης γῆς μεσημβρινοῦ, καὶ τοῦ διχοτομοῦντος αὐτῆς τὸ πλάτος παραλλήλου, καὶ ἔτι τοῦ κέντρου τῆς σφαίρας, ἵν᾽ ἐξ ἴσου τὰ ἀντικείμενα πέρατα ταῖς ὄψεσι καταλαμβάνηται καὶ φαίνηται. § 11. Πρῶτον δὲ ἕνεκεν τοῦ ποσοῦ τῆς ἐγκλίσεως τῶν τε παραλλήλων κύκλων καὶ τοῦ διὰ τῆς σημαινομένης τομῆς καὶ τοῦ κέντρου τῆς σφαίρας ὀρθοῦ πρὸς τὸν μέσον τοῦ μήκους μεσημβρινὸν ἐπιπέδου, νοείσθω ὁ μέγιστος κύκλος, ὁ τὸ φαινόμενον ἡμισφαίριον ἀφορίζων ὁ αβγδ, καὶ τοῦ μὲν διχοτομοῦντος τὸ ἡμισφαίριον μεσημβρινοῦ ἡμικύκλιον, τὸ αεγ, ἡ δὲ πρὸς τῆι ὄψει τομὴ τούτου τε καὶ τοῦ διχοτομοῦντος τὸ πλάτος παραλλήλου τὸ ε σημεῖον· καὶ γεγράφθω διὰ τοῦ ε μεγίστου κύκλου πάλιν ἡμικύκλιον ὀρθὸν πρὸς τὸ αεγ, τὸ βεδ, οὗ τὸ ἐπίπεδον δηλονότι κατὰ τὸν ἄξονα ὑποκείσεται τῶν ὄψεων. § 12. Ἀποληφθείσης τε τῆς εζ περιφερείας μοιρῶν κγ° ἡμίσους τρίτου (τοσαύτας γὰρ διέστηκεν ὁ ἰσημερινὸς τοῦ διὰ Συήνης, ὃς μέσος ἔγγιστα καθίσταται τοῦ πλάτους) γεγράφθω καὶ διὰ τοῦ ζ ἡμικύκλιον τοῦ ἰσημερινοῦ, τὸ βζδ· ἐγκεκλιμένον ἄρα φανήσεται τό, τε τοῦ ἰσημερινοῦ ἐπίπεδον καὶ τὰ τῶν ἄλλων παραλλήλων πρὸς τὸ διὰ τοῦ ἄξονος τῶν ὄψεων, τῆι εζ περιφερείαι μοιρῶν οὔσηι κγ° ἡμίσους τρίτου. {53}
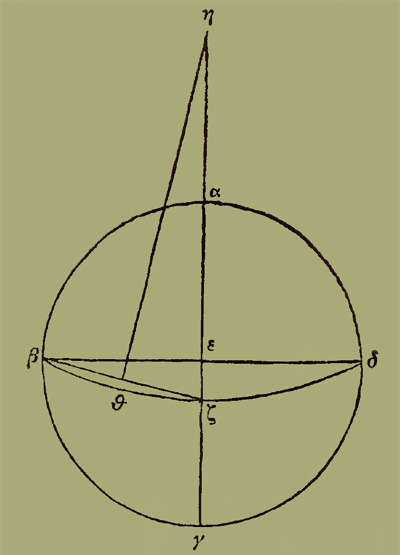
§ 13. Νοείσθωσαν δὴ αἱ αεζγ καὶ βεδ
εὐθεῖαι ἀντὶ περιφερειῶν, τῆς βε λόγον ἐχούσης πρὸς τὴν εζ, τὸν τῶν Ϟ πρὸς τὰ κγʹ Lʹ γʹ. § 14. Καὶ ἐκβληθείσης τῆς γα, πιπτέτω τὸ κέντρον, ἐν ὧι γραφήσεται τὸ βζδ τοῦ κύκλου τμῆμα, κατὰ τὸ η· προκείσθω τε εὑρεῖν τὸν τῆς ηζ πρὸς τὴν εβ λόγον· ἐζεύχθω δὴ ἡ ζβ εὐθεῖα, καὶ δίχα διαιρεθείσης αὐτῆς τῶι θ, ἐπεζεύχθω καὶ ἡ θη κάθετος δηλονότι πρὸς τὴν βζ γινομένη. § 15. Ἐπεὶ τοίνυν, οἵων ἐστὶν ἡ βε εὐθεῖα Ϟ, τοιούτων ἡ εζ ὑπόκειται κγʹ ἡμίσους γʹ, τῶν αὐτῶν ἔσται καὶ ἡ μὲν βζ ὑποτείνουσα Ϟγʹ δεκάτου, ἡ δὲ ὑπὸ βζε γωνία, τοιούτων ρνʹ καὶ γʹ, οἵων εἰσὶν αἱ δύο ὀρθαὶ τξʹ· ἡ λοιπὴ δὲ καὶ {54} ἡ ὑπὸ θηζ, τῶν αὐτῶν κθʹ γοʹ. § 16. Καὶ διὰ τοῦτο ὁ λόγος ἐστὶ τῆς ηζ πρὸς τὴν ζθ ὁ τῶν ρπαʹ ἡμίσους τρίτου πρὸς τὰ μςʹ Lʹ καὶ κʹ· καί ἐστιν οἵων ἡ θζ εὐθεῖα μςʹ Lʹ κʹ, τοιούτων ἡ βε εὐθεῖα Ϟ· ὥστε καὶ οἵων ἐστὶν ἡ μὲν εβ εὐθεῖα ἐνενήκοντα, ἡ δὲ ζε τῶν αὐτῶν κγʹ ἡμίσους τρίτου, τοιούτων ἕξομεν καὶ τὴν ηζ εὐθεῖαν ρπαʹ Lʹ γʹ· καὶ τὸ η σημεῖον, ὦι γραφήσονται πάντες οἱ ἐν τῆι ἐπιπέδωι καταγραφῆι παράλληλοι. {55}
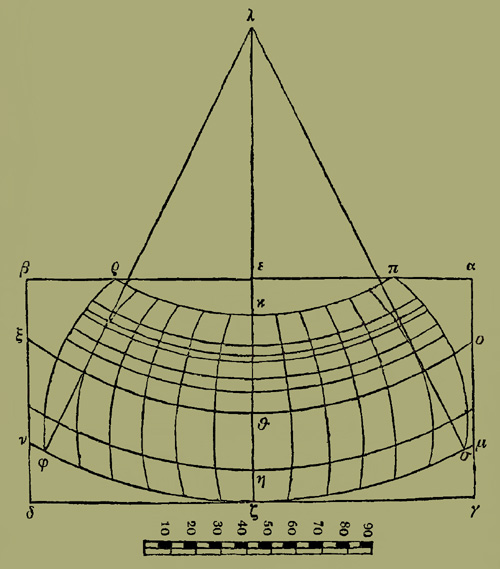
§ 17. Τούτων προληφθέντων, ἐκκείσθω ὁ αβγδ πίναξ, διπλασίαν μὲν πάλιν ἔχων τὴν αβ τῆς αγ, ἴσην δὲ τὴν αε τῆι εβ, καὶ πρὸς αὐτὰς ὀρθὴν τὴν εζ· διηιρήσθω τε ἴση τις τῆι εζ εὐθεῖαι εἰς τὰς Ϟ° τοῦ τεταρτημορίου μοίρας· ἀποληφθεισῶν δὲ τῆς μὲν ζη μοιρῶν ις° τρίτου ιβ', τῆς δὲ ηθ μοιρῶν κγ° L' τρίτου, τῆς δὲ ηκ τῶν αὐτῶν ξγ°, καὶ τοῦ η ὑποτεθέντος κατὰ τὸν ἰσημερινὸν, ἔσται καὶ τὸ μὲν θ, δι᾽ οὗ γραφήσεται ὁ διὰ Συήνης, καὶ μεταξὺ ἔγγιστα τοῦ πλάτους παράλληλος· τὸ δὲ ζ, δι᾽ οὖ γραφήσεται ὁ ἀφορίζων τὸ νότιον πέρας, καὶ ἀντικείμενος τῶι διὰ Μερόης· τὸ δὲ κ, δι᾽ οὗ γραφήσεται ὁ ἀφορίζων τὸ βόρειον πέρας καὶ διὰ Θούλης τῆς νήσου πίπτων· § 18. καὶ δὴ προσεκβαλόντες τὴν ἐπ᾽ αὐτῆς τὴν ηλ, τῶν αὐτῶν ρπαʹ [καὶ τὰ ἑξῆς τῶν αὐτῶν ρπαʹ] ἡμίσους τρίτου τμημάτων, ἢ καὶ ρπʹ μοιρῶν μόνων (οὐδενὶ γὰρ ἀξιολόγωι παρὰ τοῦτο ἡ καταγραφὴ διοίσει) κέντρωι τῶι λ, καὶ διαστήμασι τοῖς ζ καὶ θ καὶ κ, τὰς πκρ, καὶ ξθο, καὶ μζν περιφερείας γράψομεν. § 19. Ὁ μὲν τοίνυν οἰκεῖος λόγος τῆς τῶν παραλλήλων πρὸς τὸ διὰ τοῦ ἄξονος τῶν ὄψεων ἐπίπεδον ἐγκλίσεως οὕτως ἔσται τετηρημένος· ἐπειδὴ κἀνταῦθα ὁ ἄξων νεύειν τε ὀφείλει πρὸς τὸ θ καὶ ὀρθὸς εἶναι πρὸς τὸ τοῦ πίνακος ἐπίπεδον, ἵνα πάλιν ἐξ ἴσου τὰ ἀντικείμενα πέρατα τῆς καταγραφῆς τῆι ὄψει καταλαμβάνηται. § 20. Ὅπως δὲ καὶ τὸ μῆκος σύμμετρον ἦι τῶι πλάτει· (ἐπειδήπερ ἐπὶ τῆς σφαίρας οἵων ἐστὶν ὁ μέγιστος κύκλος πέντε, τοιούτων ἔγγιστα ὁ μὲν διὰ Θούλης παράλληλος συνάγεται βʹ καὶ δʹ, ὁ δὲ διὰ Συήνης τεττάρων ἡμίσους δωδεκάτου, ὁ δὲ διὰ Μερόης τεττάρων ἡμίσους {56} τρίτου)· δεῖ δ᾽ ἐφ᾽ ἑκάτερα τῆς ζκ μεσημβρινῆς εὐθείας ὀκτωκαίδεκα θέσθαι μεσημβρινοὺς διὰ τριτημορίου μιᾶς ὥρας ἰσημερινῆς εἰς συμπλήρωσιν τῶν ὑφ᾽ ὅλου τοῦ μήκους περιεχομένων ἡμικυκλίων. § 21. Ληψόμεθα τὰ ἰσοδυναμοῦντα τμήματα καθ᾽ ἕκαστον τῶν ἐκκειμένων τριῶν παραλλήλων ταῖς τοῦ τριτημορίου τῆς μιᾶς ὥρας ε° μοίραις· ἀπὸ μὲν τοῦ κ διὰ δύο καὶ τετάρτου μοιρῶν ποιούμενοι τὰς τομὰς, οἵων ἔχομεν τὴν εζ εὐθεῖαν Ϟ, ἀπὸ δὲ τοῦ δʹ Lʹ ιβʹ, ἀπὸ δὲ τοῦ [η]ζ διὰ τεσσάρων ἡμίσου τρίτου ἐπὶ τούτων αὐτῶν. § 22. Ἔπειτα γράψαντες διὰ τῶν ἰσοδυναμούντων τριῶν σημείων τὰς ἐσομένας ἀντὶ τῶν λοιπῶν μεσημβρινῶν περιφερείας, ὡς τὰς ἀφοριζούσας τὸ πᾶν μῆκος τήν τε στυ καὶ τὴν φχψ, προσαναπληρώσομεν καὶ τὰς ἀντὶ τῶν λοιπῶν παραλλήλων, κέντρωι μὲν πάλιν τῶι λ, διαστήμασι δὲ τοῖς γινομένοις ἐπὶ τῆς ζκ τμήμασι κατὰ τὰς πρὸς τὸν ἰσημερινὸν αὐτῶν διαστάσεις. § 23. Τὸ δὲ δὴ ὁμοιότερον τῶι ἐπὶ τῆς σφαίρας σχήματι τὸ ἐκ τῆς τοιαύτης καταγραφῆς ἐπὶ τὴν προτέραν αὐτόθεν ἐστὶ δῆλον. § 24. Ἐπειδὴ κἀκεῖ μενούσης τῆς σφαίρας καὶ μὴ περιστρεφομένης, ὃ καὶ τῶι πίνακι συμβέβηκεν ἐξ ἀνάγκης κατὰ τοῦ μέσου τῆς καταγραφῆς τὴν ὄψιν τετραμμένου, εἷς μὲν ὁ μέσος μεσημβρινὸς ἐν τῶι διὰ τοῦ ἄξονος τῶν ὄψεων ἐπιπέδωι πίπτων εὐθείας ἂν παρέχοι φαντασίαν· οἱ δὲ ἐφ᾽ ἑκάτερα τούτου πάντες ἐπεστραμμένοι κατὰ τὰ κοῖλα πρὸς αὐτὸν φαίνονται, καὶ μᾶλλον οἱ πλέον αὐτοῦ διεστηκότες· ὃ κἀνταῦθα παραφυλάξεταί τις μετὰ τῆς δεούσης τῶν κυρτοτήτων ἀναλογίας· καὶ ἔτι τὸ σύμμετρον τῶν τε παραλλήλων περιφερειῶν {57} πρὸς ἀλλήλας, οὐκ ἐπὶ μόνων τῶν ὑπὸ τὸν ἰσημερινὸν καὶ τὸν διὰ Θούλης, ὡς ἐκεῖ, σώζειν τὸν οἰκεῖον λόγον, ἀλλὰ καὶ ἐπὶ τῶν ἄλλων ὡς ἔνι μάλιστα ἐγγυτάτω, καθάπερ ἐξέσται πειρωμένοις σκοπεῖν. § 25. Καὶ τοῦ ὅλου πλάτους πρὸς ὅλον τὸ μῆκος, οὐκ ἐπὶ μόνου πάλιν τοῦ διὰ τῆς Ῥοδίας γραφομένου παραλλήλου καθάπερ ἐκεῖ, σχεδὸν δὲ ἐπὶ πάντων ἁπλῶς. § 26. Ἐὰν γὰρ κἀνταῦθα διαγάγωμεν τὴν σωυ εὐθεῖαν ὡς ἐπὶ τοῦ προτέρου σχήματος, ἥτε θω περιφέρεια ἐλάττονα δηλονότι ποιήσει λόγον πρὸς τὰς ζσ καὶ κυ, τοῦ προσήκοντος ἐν ταύτηι τῆι καταγραφῆι λόγου, ὃς εἴληπτο καθ᾽ ὅλην τὴν θτ, νοουμένην κατὰ τὸν ἰσημερινόν. § 27. Ἐάν τε ταύτην σύμμετρον ποιήσωμεν τῆι κζ τοῦ πλάτους διαστάσει, αἱ ζσ καὶ κυ μείζους ἔσονται τῶν πρὸς τὴν ζκ συμμέτρων, ὥσπερ καὶ ἡ θτ· ἐάν τε τὰς ζσ καὶ κυ τηρῶμεν τῆι ζκ συμμέτρους, ἡ θω ἐλάττων ἔσται τῆς πρὸς τὴν κζ συμμετρίας, καθάπερ καὶ τῆς [θν]θτ.
§ 28. Τούτοις μὲν οὖν ἂν ἡ μέθοδος αὕτη πλεονεκτοίη τῆς προτέρας· λείποιτο δ᾽ ἂν ἐκείνης καὶ αὕτη τῶι προχείρωι τῆς καταγραφῆς, ἐπειδήπερ ἐκεῖ μὲν ἦν ἀπὸ τῆς τοῦ κανονίου παραγωγῆς τε καὶ παραφορᾶς, ἑνὸς μόνου τῶν παραλλήλων γραφέντος καὶ διαιρεθέντος, ἐντάσσειν ἕκαστον τῶν τόπων· ἐνθάδε δὲ μηκέτι τοῦ τοιούτου προχωροῦντος διὰ τὰς τῶν μεσημβρινῶν γραμμῶν πρὸς τὴν μέσην ἐπιστροφὰς, πάντας τε δεῖ {58} τοὺς κύκλους προσκαταγράφειν, καὶ τὰς μεταξὺ τῶν πλινθίων πιπτούσας θέσεις τῶι πρὸς ὅλας τὰς περιεχούσας πλευράς, διὰ τῶν σημαινομένων μερῶν ἐπιλογισμῶι καταστοχάζεσθαι. § 29. Τούτων δὲ οὕτως ἐχόντων, προτιμητέον μὲν ἔμοιγε κἀνταῦθα καὶ πανταχῆ τὸ βέλτιον καὶ ἐπιπονώτερον τοῦ χείρονος καὶ ῥάιονος, τηρητέον δὲ ὅμως ἀμφοτέρας τὰς μεθόδους κατατεταγμένας, ἕνεκεν τῶν ἐπὶ τὴν προχειροτέραν αὐτῶν ὑπὸ ῥαιστώνης κατενεχθησομένων.
§ 30. Οἵων ἐστὶν ὁ ἰσημερινὸς εʹ, τοιούτων ὁ διὰ Μερόης, δʹ Lʹ γʹ· ὡς λόγον ἔχειν πρὸς αὐτόν, ὃν τὰ λʹ πρὸς κθʹ.
§ 31. Οἵων ἐστὶν ὁ ἰσημερινὸς εʹ, τοιούτων ὁ διὰ Συήνης, δʹ Lʹ ιβʹ· ὡς λόγον ἔχειν πρὸς αὐτόν, ὃν τὰ ξʹ πρὸς νεʹ· τουτέστιν ὃν τὰ ιβʹ, πρὸς τα ιαʹ.
§ 32. Οἵων ἐστὶν ὁ ἰσημερινὸς εʹ, τοιούτων ὁ διὰ Ῥόδου δʹ· ὡς λόγον ἔχειν πρὸς αὐτόν τὸν ἐπιτέταρτον.
§ 33. Οἵων ἐστὶν ὁ ἰσημερινὸς εʹ, τοιούτων ὁ διὰ Θούλης βʹ δʹ· ὡς λόγον ἔχειν πρὸς αὐτόν, ὃν τὰ κʹ πρὸς τα θʹ.
|



