| |
αʹ.
Πᾶς κύκλος ἴσος ἐστι τριγώνωι ὀρθογωνίωι, οὗ ἡ μὲν ἐκ τοῦ κέντρου ἴση μιᾶι τῶν περὶ τὴν ὀρθήν, ἡ δὲ περίμετρος τῆι βάσει.
Ἐχέτω ὁ ΑΒΓΔ κύκλος τριγώνωι τῶι Ε, ὡς ὑπόκειται· λέγω ὅτι ἴσος ἐστίν.

Εἰ γὰρ δυνατόν, ἔστω μείζων ὁ κύκλος, καὶ ἐγγεγράφθω τὸ ΑΓ τετράγωνον, καὶ τετμήσθωσαν αἱ περιφέρειαι δίχα, καὶ ἔστω τὰ τμήματα ἤδη ἐλάσσονα τῆς ὑπεροχῆς, ἧι ὑπερέχει ὁ κύκλος τοῦ τριγώνου· τὸ εὐθύγραμμον ἄρα ἔτι τοῦ τριγώνου ἐστὶ μεῖζον. Εἰλήφθω κέντρον τὸ Ν καὶ κάθετος ἡ ΝΞ· ἐλάσσων ἄρα ἡ ΝΞ τῆς τοῦ τριγώνου πλευρᾶς. Ἔστιν δὲ καὶ ἡ περίμετρος τοῦ εὐθυγράμμου τῆς λοιπῆς ἐλάττων, ἐπεὶ καὶ τῆς τοῦ κύκλου περιμέτρου· ἔλαττον ἄρα τὸ εὐθύγραμμον τοῦ Ε τριγώνου· ὅπερ ἄτοπον.

Ἔστω δὲ ὁ κύκλος, εἰ δυνατόν, ἐλάσσων τοῦ Ε τριγώνου, καὶ περιγεγράφθω τὸ τετράγωνον, καὶ τετμήσθωσαν αἱ περιφέρειαι δίχα, καὶ ἤχθωσαν ἐφαπτόμεναι διὰ τῶν σημείων· ὀρθὴ ἄρα ἡ ὑπὸ ΟΑΡ. Ἡ ΟΡ ἄρα τῆς ΜΡ ἐστὶν μείζων· ἡ γὰρ ΡΜ τῆι ΡΑ ἴση ἐστί· καὶ τὸ ΡΟΠ τρίγωνον ἄρα τοῦ ΟΖΑΜ σχήματος μεῖζόν ἐστιν ἢ τὸ ἥμισυ. Λελείφθωσαν οἱ τῶι ΠΖΑ τομεῖ ὅμοιοι ἐλάσσους τῆς ὑπεροχῆς, ἧι ὑπερέχει τὸ Ε τοῦ ΑΒΓΔ κύκλου· ἔτι ἄρα τὸ περιγεγραμμένον εὐθύγραμμον τοῦ Ε ἐστὶν ἔλασσον· ὅπερ ἄτοπον· ἔστιν γὰρ μεῖζον, ὅτι ἡ μὲν ΝΑ ἴση ἐστὶ τῆι καθέτωι τοῦ τριγώνου, ἡ δὲ περίμετρος μείζων ἐστὶ τῆς βάσεως τοῦ τριγώνου, Ἴσος ἄρα ὁ κύκλος τῶι Ε τριγώνωι.
βʹ.
Ὁ κύκλος πρὸς τὸ ἀπὸ τῆς διαμέτρου τετράγωνον λόγον ἔχει, ὃν ια πρὸς ιδ.
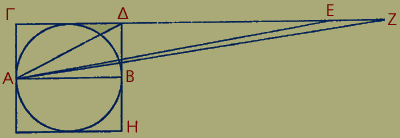
Ἔστω κύκλος, οὗ διάμετρος ἡ ΑΒ, καὶ περιγεγράφθω τετράγωνον τὸ ΓΗ, καὶ τῆς ΓΔ διπλῆ ἡ ΔΕ, ἕβδομον δὲ ἡ ΕΖ τῆς ΓΔ. Ἐπεὶ οὖν τὸ ΑΓΕ πρὸς τὸ ΑΓΔ λόγον ἔχει, ὃν κα πρὸς ζ, πρὸς δὲ τὸ ΑΕΖ τὸ ΑΓΔ λόγον ἔχει, ὃν ἑπτὰ πρὸς ἕν, τὸ ΑΓΖ πρὸς τὸ ΑΓΔ ἐστίν, ὡς κβ πρὸς ζ. Ἀλλα τοῦ ΑΓΔ τετραπλάσιόν ἐστι τὸ ΓΗ τοτράγωνον, τὸ δὲ ΑΓΔΖ τρίγωνον τῶι ΑΒ κύκλωι ἴσον ἐστίν [ἐπεί ἡ μὲν ΑΓ κάθετος ἴση ἐστὶ τῆι ἐκ τοῦ κέντρου, ἡ δὲ βάσις τῆς διαμέτρου τριπλασίων καὶ τῶι ζ' ἔγγιστα ὑπερέχουσα δειχθήσεται]· ὁ κύκλος οὖν πρὸς τὸ ΓΗ τετράγωνον λόγον ἔχει, ὃν ια πρὸς ιδ.
γʹ.
Παντὸς κύκλου ἡ περίμετρος τῆς διαμέτρου τριπλασίων ἐστὶ καὶ ἔτι ὑπερέχει ἐλάσσονι μὲν ἢ ἑβδόμωι μέρει τῆς διαμέτρου, μείζονι δὲ ἢ δέκα ἑβδομηκοστομόνοις.
Ἔστω κύκλος καὶ διάμετρος ἡ ΑΓ καὶ κέντρον τὸ Ε καὶ ἡ ΓΛΖ ἐφαπτομένη καὶ ἡ ὑπὸ ΖΕΓ τρίτου ὀρθῆς· ἡ ΕΖ ἄρα πρὸς ΖΓ λόγον ἔχει, ὃν τς πρὸς ρνγ, ἡ δὲ ΕΓ πρὸς [τὴν] ΓΖ λόγον ἔχει, ὃν σξε πρὸς ρνγ. Τετμήσθω οὖν ἡ ὑπὸ ΖΕΓ δίχα τῆι ΕΗ· ἔστιν ἄρα, ὡς ἡ ΖΕ πρὸς ΕΓ, ἡ ΖΗ πρὸς ΗΓ [καὶ ἐναλλὰξ καὶ συνθέντι]. Ὡς ἄρα συναμψότερος ἡ ΖΕ, ΕΓ πρὸς ΖΓ, ἡ ΕΓ πρὸς ΓΗ· ὥστε ἡ ΓΕ πρὸς ΓΗ μείζονα λόγον ἔχει ἤπερ φοα πρὸς ρνγ. Ἡ ΕΗ ἄρα πρὸς ΗΓ δυνάμει λόγον ἔχει, ὃν λδ/Μ ,θυν πρὸς β/Μ ,γυθ· μήκει ἄρα, ὃν φϞα η' πρὸς ρνγ.

Πάλιν δίχα ἡ ὑπό ΗΕΓ τῆι ΕΘ· διὰ τὰ αὐτὰ ἄρα ἡ ΕΓ πρὸς ΓΘ μείζονα λόγον ἔχει ἢ ὃν ,αρξβ η' πρὸς ρνγ· ἡ ΘΕ ἄρα πρός ΘΓ μείζονα λόγον ἔχει ἢ ὃν ,αροβ η' πρὸς ρνγ. Ἔτι δίχα ἡ ὑπὸ ΘΕΓ τῆι ΕΚ· ἡ ΕΓ ἄρα πρὸς ΓΚ μείζονα λόγον ἔχει ἢ ὃν ,βτλδ δ' πρὸς ρνγ· ἡ ΕΚ ἄρα πρὸς ΓΚ μείζονα ἢ ὃν ,βτλθ δ' πρὸς ρνγ. Ἔτι δίχα ἡ ὑπὸ ΚΕΓ τῆι ΛΕ· ἡ ΕΓ ἄρα πρὸς ΛΓ μείζονα [μήκει] λόγον ἔχει ἤπερ τὰ ,δχογ L' πρὸς ρνγ. Ἐπεὶ οὖν ἡ ὑπὸ ΖΕΓ τρίτου οὖσα ὀρθῆς τέτμηται τετράκις δίχα, ἡ ὑπὸ ΛΕΓ ὀρθῆς ἐστι μη'. Κείσβω οὖν αὐτῆι ἴση πρὸς τῶι Ε ἡ ὑπὸ ΓΕΜ· ἡ ἄρα ὑπὸ ΛΕΜ ὀρθῆς ἐστι κδ'. Καὶ ἡ ΛΜ ἄρα εὐθεῖα τοῦ περὶ τὸν κύκλον ἐστὶ πολυγώνου πλευρὰ πλευρὰς ἔχοντος Ϟς. Ἐπεὶ οὖν ἡ ΕΓ πρὸς τὴν ΓΛ ἐδείχθη μείζονα λόγον ἔχουσα ἤπερ ,δχογ L' πρὸς ρνγ, ἀλλὰ τῆς μὲν ΕΓ διπλῆ ἡ ΑΓ, τῆς δὲ ΓΛ διπλασίων ἡ ΛΜ, καὶ ἡ ΑΓ ἄρα πρὸς τὴν τοῦ Ϟς γώνου περίμετρον μείζονα λόγον ἔχει ἤπερ ,δχογ L' πρὸς α/Μ ,δχπη. Καί ἐστιν τριπλασία, καὶ ὑπερέχουσιν χξζ L', ἅπερ τῶν ,δχογ L' ἐλάττονά ἐστιν ἢ τὸ ἕβδομον· ὥστε τὸ πολύγωνον τὸ περὶ τὸν κύκλον τῆς διαμέτρου ἐστὶ τριπλάσιον καὶ ἐλάττονι ἢ τῶι ἑβδόμωι μέρει μεῖζον· ἡ τοῦ κύκλου ἄρα περίμετρος πολὺ μάλλον ἐλάσσων ἐστὶν ἢ τριπλασίων καὶ ἑβδόμωι μέρει μείζων.

Ἔστω κύκλος καὶ διάμετρος ἡ ΑΓ, ἡ δὲ ὑπὸ ΒΑΓ τρίτου ὀρθῆς· ἡ ΑΒ ἄρα πρὸς ΒΓ ἐλάσσονα λόγον ἔχει ἢ ὃν ,ατνα πρὸς ψπ [ἡ δὲ ΑΓ πρὸς ΓΒ, ὃν ,αφξ πρὸς ψπ]. Δίχα ἡ ὑπὸ ΒΑΓ τῆι ΑΗ. Ἐπεὶ οὖν ἴση ἐστὶν ἡ ὑπὸ ΒΑΗ τῆι ὑπὸ ΗΓΒ, ἀλλὰ καὶ τῆι ὑπὸ ΗΑΓ, καὶ ἡ υπὸ ΗΓΒ τῆι ὑπὸ ΗΑΓ ἐστὶν ἴση. Καὶ κοινὴ ἡ ὑπὸ ΑΗΓ ὀρθή· καὶ τρίτη ἄρα ἡ ὑπὸ ΗΖΓ τρίτηι τῆι ὑπὸ ΑΓΗ ἴση. Ἰσογώνιον ἄρα τὸ ΑΗΓ τῶι ΓΗΖ τριγώνωι· ἔστιν ἄρα, ὡς ἡ ΑΗ πρὸς ΗΓ, ἡ ΓΗ πρὸς ΗΖ καὶ ἡ ΑΓ πρὸς ΓΖ. Ἀλλ' ὡς ἡ ΑΓ πρὸς ΓΖ, [καί] συναμφότερος ἡ ΓΑΒ πρὸς ΒΓ· καὶ ὡς συναμφότερος ἄρα ἡ ΒΑΓ πρὸς ΒΓ, ἡ ΑΗ πρὸς ΗΓ. Διὰ τοῦτο οὖν ἡ ΑΗ πρὸς [τὴν] ΗΓ ἐλάσσονα λόγον ἔχει ἤπερ βϠια πρὸς ψπ, ἡ δὲ ΑΓ πρὸς τὴν ΓΗ ἐλάσσονα ἢ ὃν ,γιγ L' δ' πρὸς ψπ. Δίχα ἡ ὑπὸ ΓΑΗ τῆι ΑΘ· ἡ ΑΘ ἄρα διὰ τὰ αὐτὰ πρὸς τὴν ΘΓ ἐλάσσονα λόγον ἔχει ἢ ὃν ,εϠκδ L' δ' πρὸς ψπ ἢ ὃν ,αωκγ πρὸς σμ· ἑκατέρα γὰρ ἑκατέρας δ ιγ'· ὥστε ἡ ΑΓ πρὸς τὴν ΓΘ ἢ ὃν ,αωλη θ ια' πρὸς σμ. Ἔτι δίχα ἡ ὑπὸ ΘΑΓ τῆι ΚΑ· καὶ ἡ ΑΚ πρὸς τὴν ΚΓ ἐλάσσονα [ἄρα] λόγον ἔχει ἢ ὃν ,αζ πρὸς ξς· ἑκατέρα γὰρ ἑκατέρας ια μ'. Ἡ ΑΓ ἄρα πρὸς [τὴν] ΚΓ ἢ ὃν ,αθ ς' πρὸς ,ξς. Ἔτι δίχα ἡ ὑπὸ ΚΑΓ τῆι ΛΑ· ἡ ΑΛ ἄρα πρὸς [τὴν] ΛΓ ἐλάσσονα λόγον ἔχει ἢ ὃν τὰ ,βιζ ς' πρὸς ξς, ἡ δὲ ΑΓ πρὸς ΓΛ ἐλάσσονα ἢ τὰ ,βιζ δ' πρὸς ξς. Ἀνάπαλιν ἄρα ἡ περίμετρος τοῦ πολυγώνου πρὸς τὴν διάμετρον μείζονα λόγον ἔχει ἤπερ ,ςτλς πρὸς ,βιζ δ', ἅπερ τῶν ,βιζ δ' μείζονά ἐστιν ἢ τριπλασίονα καὶ δέκα οα'· καὶ ἡ περίμετρος ἄρα τοῦ Ϟς γώνου τοῦ ἐν τῶι κύκλωι τῆς διαμέτρου τριπλασίων ἐστὶ καὶ μείζων ἢ ι οα'· ὥστε καὶ ὁ κύκλος ἔτι μᾶλλον τριπλασίων ἐστὶ καὶ μείζων ἢ ι οα'.
Ἡ ἄρα τοῦ κύκλου περίμετρος τῆς διαμέτρου τριπλασίων ἐστὶ καὶ ἐλάσσονι μὲν ἢ ἑβδόμωι μέρει, μείζονι δὲ ἢ ι οα' μείζων.
|




