| |

Function und Begriff.
Vortrag
gehalten in der Sitzung vom 9. Januar 1891 der
Jenaischen Gesellschaft für Medicin und Naturwissenschaft
von
Dr. G. Frege
Professor an der Universität Jena.
Jena,
Verlag von Hermann Pohle
Grossh. Hofbuchdrucker
1891.
―――――――――
Vorwort.
Ich gebe hiermit einen Vortrag gesondert heraus in der Hoffnung, dass er so einige Leser finden werde, denen er unter den Abhandlungen der Jenaischen Gesellschaft für Medicin und Naturwissenschaft unbekannt bleiben würde. Es ist meine Absicht, in nächster Zeit, wie ich schon früher angedeutet habe, darzulegen, wie ich die grundlegenden Definitionen der Arithmetik in meiner Begriffsschrift ausdrücke, und wie ich daraus Beweise allein mit meinen Zeichen führe. Für diesen Zweck ist es mir von Werth, mich auf diesen Vortrag berufen zu können, um nicht genöthigt zu sein, mich dort in Erörterungen einzulassen, die vielleicht Manchen als nicht unmittelbar zur Sache gehörig missfallen würden, von Anderen hingegen vermisst werden könnten. Mein Vortrag wendet sich, wie es der Ort mit sich brachte, nicht nur an Mathematiker; und ich habe mich einer so allgemeinverständlichen Ausdrucksweise zu bedienen gesucht, als es die verfügbare Zeit und der Gegenstand zuliessen. Möge denn hierdurch in weiteren Kreisen der Gelehrten, insbesondere auch bei Logikern, Interesse für die Sache geweckt werden.
―――――――――
Vor längerer Zeit 1) hatte ich die Ehre, in dieser Gesellschaft über das Ganze von Bezeichnungen vorzutragen, das ich Begriffsschrift genannt habe. Heute möchte ich nun diese Sache von einer anderen Seite her beleuchten und einige Ergänzungen und neue Fassungen mittheilen, deren Nothwendigkeit sich mir seitdem ergeben hat. Es kann sich dabei nicht um eine vollständige Darlegung meiner Begriffsschrift, sondern nur darum handeln, einige Grundgedanken ins Licht zu setzen.
Ich gehe von dem aus, was in der Mathematik Function genannt wird. Dieses Wort hat nicht gleich anfangs eine so weite Bedeutung gehabt, als es später erlangt hat. Es wird gut sein, unsere Betrachtung bei der ursprünglichen Gebrauchsweise zu beginnen und erst dann die späteren Erweiterungen ins Auge zu fassen. Ich will zunächst nur von Functionen eines einzigen Arguments sprechen. Ein wissenschaftlicher Ausdruck erscheint da zuerst in seiner ausgeprägten Bedeutung, wo man seiner zum Aussprechen einer Gesetzmässigkeit bedarf. Dieser Fall trat für die {2} Function ein bei der Entdeckung der höheren Analysis. Da zuerst handelte es sich darum, Gesetze aufzustellen, die von Functionen im Allgemeinen gelten. In die Zeit der Entdeckung der höheren Analysis ist also zurückzugehen, wenn man wissen will, was zuerst in der Mathematik unter dem Worte «Function» verstanden wurde. Auf diese Frage erhält man wohl als Antwort: «unter einer Function von x wurde verstanden ein Rechnungsausdruck, der x enthält, eine Formel, die den Buchstaben x einschliesst». Danach würde z. B. der Ausdruck
2 · x3 + x
eine Function von x,
2 · 23 + 2
eine Function von 2 sein. Diese Antwort kann nicht befriedigen, weil dabei Form und Inhalt, Zeichen und Bezeichnetes nicht unterschieden werden, ein Fehler, dem man freilich jetzt in mathematischen Schriften, selbst von namhaften Verfassern sehr oft begegnet. Ich habe schon früher 2) auf die Mängel der gangbaren formalen Theorien in der Arithmetik hingewiesen. Man spricht da von Zeichen, die keinen Inhalt haben, noch haben sollen, legt ihnen dann aber doch Eigenschaften bei, die nur einem Inhalte des Zeichens vernünftigerweise zukommen können. So auch hier: ein blosser Ausdruck, die Form für einen Inhalt kann {3} das Wesen der Sache nicht sein, sondern nur der Inhalt selbst. Was ist nun der Inhalt, die Bedeutung von «2 · 23 + 2»? Dieselbe wie von «18» oder von «3 · 6». In der Gleichung 2 · 23 + 2 = 18 wird ausgedrückt, dass die Bedeutung der rechtsstehenden Zeichenverbindung dieselbe sei wie die der linksstehenden. Ich muss hier der Ansicht entgegentreten, dass z. B. 2 + 5 und 3 + 4 zwar gleich, aber nicht dasselbe seien. Es liegt dieser Meinung wieder jene Verwechselung von Form und Inhalt, von Zeichen und Bezeichnetem zu Grunde. Es ist ebenso, als ob man das wohlriechende Veilchen als verschieden von Viola odorata ansehen wollte, weil die Namen verschieden klingen. Die Verschiedenheit der Bezeichnung kann allein nicht hinreichen, eine Verschiedenheit des Bezeichneten zu begründen. Hier ist die Sache nur dadurch weniger durchsichtig, dass die Bedeutung des Zahlzeichens 7 nichts sinnlich Wahrnehmbares ist. Die jetzt sehr verbreitete Neigung, nichts als Gegenstand anzuerkennen, was nicht mit den Sinnen wahrgenommen werden kann, verleitet dann dazu, die Zahlzeichen selbst für die Zahlen, für die eigentlichen Gegenstände der Betrachtung zu halten 3); und dann wären ja freilich 7 und 2 + 5 verschieden. Aber eine solche Auffassung ist nicht zu halten, weil man gar nicht {4} von irgendwelchen arithmetischen Eigenschaften der Zahlen sprechen kann, ohne auf die Bedeutung der Zahlzeichen zurückzugehen. Die Eigenschaft der 1 z. B., mit sich selbst multiplicirt sich selbst wieder zu ergeben, wäre eine reine Erdichtung; keine noch so weit getriebene mikroskopische oder chemische Untersuchung könnte jemals diese Eigenschaft an dem unschuldigen Gebilde entdecken, das wir Zahlzeichen Eins nennen. Man spricht vielleicht von einer Definition; aber keine Definition ist in der Weise schöpferisch, dass sie einem Dinge Eigenschaften verleihen könnte, die es nun einmal nicht hat, ausser der einen, das auszudrücken und zu bezeichnen, wofür die Definition es als Zeichen einführt 4). Dagegen haben die Gebilde, die wir Zahlzeichen nennen, physikalische und chemische Eigenschaften, die von dem Schreibmittel abhangen. Man könnte sich denken, dass einmal ganz neue Zahlzeichen eingeführt würden, wie die arabischen z. B. die römischen verdrängt haben. Niemand wird im Ernste annehmen, dass man dadurch ganz neue Zahlen bekäme, ganz neue Gegenstände der Arithmetik mit bisher noch unerforschten Eigenschaften. Wenn man also von den Zahlzeichen ihre Bedeutungen unterscheiden muss, so wird man auch den Ausdrücken «2», «1 + 1», «3 – 1», «6 : 3» dieselbe Bedeutung {5} zuerkennen müssen; denn es ist gar nicht abzusehen, worin der Unterschied bestehen sollte. Man sagt vielleicht: 1 + 1 ist eine Summe , aber 6 : 3 ein Quotient. Was ist aber 6 : 3? die Zahl, welche mit 3 multiplicirt 6 ergiebt. «Die Zahl», nicht «eine Zahl» heisst es; mit dem bestimmten Artikel deutet man an, dass es nur eine einzige giebt. Nun ist
(1 + 1) + (1 + 1) + (1 + 1) = 6,
und also ist (1 + 1) eben die Zahl, welche als (6 : 3) bezeichnet wurde. Die verschiedenen Ausdrücke entsprechen verschiedenen Auffassungen und Seiten, aber doch immer derselben Sache. Die Gleichung x2 = 4 würde sonst nicht nur die beiden Wurzeln 2 und –2, sondern auch (1 + 1) und unzählige andere erhalten, die von einander verschieden, wenn auch in gewisser Hinsicht einander ähnlich wären. Indem man nur zwei reelle Wurzeln anerkennt, verwirft man die Ansicht, das Gleichheitszeichen bedeute kein völliges Zusammenfallen, sondern nur eine theilweise Uebereinstimmung. Halten wir daran fest, so sehen wir, dass die Ausdrücke
«2 · 13 +1»,
«2 · 23 + 2»,
«2 · 43 + 4»
Zahlen bedeuten, nämlich 3, 18, 132. Wenn nun die Function wirklich nur Bedeutung eines Rechnungsausdrucks wäre, so wäre sie eben eine Zahl; und etwas Neues hätten wir damit für die Arithmetik nicht gewonnen. Nun pflegt man freilich bei dem Worte «Function» an Ausdrücke zu denken, {6} in denen eine Zahl durch den Buchstaben x nur unbestimmt angedeutet ist, wie etwa
«2 · x3 + x»;
aber damit ist nichts geändert; denn dieser Ausdruck deutet dann eine Zahl auch nur unbestimmt an; und ob ich ihn hinschreibe, oder nur «x», macht keinen wesentlichen Unterschied.
Dennoch werden wir eben durch die Schreibung mit dem unbestimmt andeutenden «x» auf die richtige Fassung hingeleitet. Man nennt x das Argument der Function und erkennt in
«2 · 13 +1»,
«2 · 43 + 4»,
«2 · 53 + 5»
dieselbe Function wieder, nur mit verschiedenen Argumenten, nämlich 1, 4 und 5. Daraus ist zu ersehen, dass in dem Gemeinsamen jener Ausdrücke das eigentliche Wesen der Function liegt; d. h. also in dem, was in
«2 · x3 + x»;
noch ausser dem «x» vorhanden ist, was wir etwa so schreiben könnten
«2 · ()3 + ()».
Es kommt mir darauf an, zu zeigen, dass das Argument nicht mit zur Function gehört, sondern mit der Function zusammen ein vollständiges Ganzes bildet; denn die Function für sich allein ist unvollständig, ergänzungsbedürftig oder ungesättigt zu nennen. Und dadurch unterscheiden sich die Functionen von den Zahlen von Grund aus. Und aus diesem Wesen der Function erklärt es sich, {7} dass wir einerseits in «2 · 13 + 1» und «2 · 23 + 2» dieselbe Function erkennen, obwohl diese Ausdrücke verschiedene Zahlen bedeuten, während wir andererseits in «2 · 13 + 1» und «4 – 1» trotz des gleichen Zahlenwerthes nicht dieselbe Function wiederfinden. Wir sehen nun auch, wie man leicht dazu verführt wird, grade in der Form des Ausdrucks das Wesentliche der Function zu sehen. In dem Ausdrucke erkennen wir die Function dadurch, dass wir ihn zerlegt denken; und eine solche mögliche Zerlegung wird durch seine Bildung nahe gelegt.
Die beiden Theile, in welche der Rechnungsausdruck so zerlegt wird, das Zeichen des Arguments und der Ausdruck der Function sind ungleichartig, da ja das Argument eine Zahl , ein in sich abgeschlossenes Ganzes ist, was die Function nicht ist. Man kann dies vergleichen mit der Theilung einer Strecke durch einen Punkt. Man ist dann geneigt, den Theilungspunkt zu beiden Theilstrecken zu rechnen. Wenn man aber die Theilung rein vornehmen will, nämlich so, dass nichts doppelt gerechnet wird und nichts ausfällt, so darf man den Theilpunkt nur zu der einen Theilstrecke rechnen. Diese wird dadurch völlig in sich abgeschlossen und ist dem Argumente zu vergleichen, während der anderen etwas fehlt. Der Theilpunkt nämlich, den man ihren Endpunkt nennen könnte, gehört nicht zu ihr. Erst dadurch, dass man sie durch diesen Endpunkt oder eine Strecke mit zwei Endpunkten ergänzt, erhält man aus ihr etwas Vollständiges. Wenn ich nun z. B. sage «die Function 2 · x3 + x», so ist x nicht als {8} zur Function gehörig zu betrachten, sondern dieser Buchstabe dient nur dazu, die Art der Ergänzungsbedürftigkeit anzudeuten, indem er die Stellen kenntlich macht, wo das Zeichen des Arguments einzutreten hat.
Wir nennen nun das, wozu die Function durch ihr Argument ergänzt wird, den Werth der Function für dies Argument. So ist z. B. 3 der Werth der Function 2 · x2 + x für das Argument 1, weil wir haben 2 · 12 + 1 = 3.
Es giebt Functionen wie z. B. 2 + x – x oder 2 + 0 · x, deren Werth immer derselbe ist, was auch ihr Argument sei; wir haben 2 = 2 + x – x und 2 = 2 + 0 · x. Wenn man nun das Argument mit zur Function rechnete, so würde man die Zahl 2 für diese Function halten. Aber dies ist unrichtig. Obwohl hier der Werth der Function immer 2 ist, so ist die Function selbst doch von 2 zu unterscheiden; denn der Ausdruck einer Function muss immer eine oder mehrere Stellen aufweisen, welche zur Ausfüllung durch das Zeichen des Arguments bestimmt sind.
Die Methode der analytischen Geometrie bietet nun ein Mittel, uns die Werthe einer Function für verschiedene Argumente anschaulich zu machen. Indem wir nämlich das Argument als Zahlenwerth einer Abscisse und den zugehörigen Werth der Function als Zahlenwerth der Ordinate eines Punktes betrachten, erhalten wir eine Gesammtheit von Punkten, die sich der Anschauung in den gewöhnlichen Fällen als Curve darstellt. Jeder Curvenpunkt entspricht einem Argumente mit dem zugehörigen Functionswerthe. {9}
So giebt z. B.
y = x2 – 4x
eine Parabel, wobei «y» den Werth der Function und den Zahlenwerth der Ordinate ebenso andeutet wie «x» das Argument und den Zahlenwerth der Abscisse. Vergleichen wir hiermit die Function
x(x – 4),
so finden wir, dass sie allgemein für dasselbe Argument denselben Werth hat wie jene. Wir haben allgemein
x2 – 4x = x(x – 4),
welche Zahl auch für x genommen werde. Daher ist die Curve, die wir aus
y = x2 – 4x
erhalten, dieselbe wie die aus
y = x(x – 4)
hervorgehende. Ich spreche das so aus: die Function x(x – 4) hat denselben Werthverlauf wie die Function x2 – 4x.
Wenn wir schreiben
x2 – 4x = x(x – 4),
so haben wir nicht eine Function der anderen, sondern nur die Functionswerthe einander gleich gesetzt. Und wenn wir diese Gleichung so verstehen, dass sie gelten soll, was für ein Argument auch für x eingesetzt werden möge, so haben wir damit die Allgemeinheit einer Gleichung ausgedrückt. Wir können dafür aber auch sagen «der Werthverlauf der Function x(x – 4) ist gleich dem {10} der Function x2 – 4x und haben darin eine Gleichung zwischen Werthverläufen. Dass es nun möglich ist, die Allgemeinheit einer Gleichung zwischen Functionswerthen als eine Gleichung aufzufassen, nämlich als eine Gleichung zwischen Werthverläufen, ist, wie mir scheint, nicht zu beweisen, sondern muss als logisches Grundgesetz angesehen werden 5).
Es mag nun auch eine kurze Bezeichnungsweise für den Werthverlauf einer Function eingeführt werden. Zu dem Zwecke ersetze ich das Zeichen des Arguments in dem Ausdrucke der Function durch ein griechisches Vokalzeichen, schliesse das Ganze in Klammern ein und schicke ihm denselben griechischen Buchstaben mit einem Spiritus lenis vorher. Danach ist z. B.
ἐ (ε2 – 4ε)
der Werthverlauf der Function x2 – 4x und
ἀ (α · (α – 4))
der Werthverlauf der Function x(x – 4), so dass wir in
«ἐ (ε2 – 4ε) = ἀ (α · (α – 4))»
den Ausdruck dafür haben, dass der erste Werthverlauf derselbe wie der zweite ist. Die griechischen Buchstaben sind absichtlich verschieden gewählt, um anzudeuten, dass nichts dazu nöthigt, denselben zu nehmen. {11}
«x2 – 4x = x(x – 4)»
drückt zwar denselben Sinn aus, wenn wir es wie oben verstehen, aber in anderer Weise. Es stellt den Sinn dar als Allgemeinheit einer Gleichung, während der neu eingeführte Ausdruck einfach eine Gleichung ist, deren rechte Seite sowohl wie die linke eine in sich abgeschlossene Bedeutung hat. In
«x2 – 4x = x(x – 4)»
deutet die linke Seite, allein betrachtet, nur unbestimmt eine Zahl an und ebenso die rechte Seite. Wenn wir blos «x2 – 4x» hätten, so könnten wir dafür auch «y2 – 4y» schreiben, ohne den Sinn zu ändern; denn «y» deutet ebenso wie «x» nur unbestimmt eine Zahl an. Wenn wir aber beide Seiten zu einer Gleichung vereinigen, so müssen wir beiderseits denselben Buchstaben wählen und drücken dadurch etwas aus, was weder die linke Seite für sich, noch die rechte Seite, noch das Gleichheitszeichen enthält, nämlich eben die Allgemeinheit, freilich die Allgemeinheit einer Gleichung, aber doch in erster Linie eine Allgemeinheit.
Wie man eine Zahl unbestimmt durch einen Buchstaben andeutet, um Allgemeinheit auszudrücken, hat man auch das Bedürfniss, eine Function unbestimmt durch Buchstaben anzudeuten. Man bedient sich dazu meistens der Buchstaben f und F in der Weise, dass in «f (x)» und «F(x)» x das Argument vertritt. Hier kommt die Ergänzungs-bedürftigkeit der Function dadurch zum Ausdruck, dass der Buchstabe f oder F eine Klammer {12} mit sich führt, deren Innenraum zur Aufnahme des Argumentzeichens bestimmt ist. Danach deutet
«ἐ f (ε)»
den Werthverlauf einer Function an, die unbestimmt gelassen ist.
Wie ist nun die Bedeutung des Wortes Function beim Fortschreiten der Wissenschaft erweitert worden? Man kann dabei zwei Richtungen unterscheiden.
Erstens nämlich ist der Kreis der Rechnungsarten erweitert worden , die zur Bildung einer Function beitragen. Zu der Addition, Multiplication, Potenzierung und deren Umkehrungen sind die verschiedenen Arten des Grenzüberganges hinzugekommen, ohne dass man allerdings immer ein klares Bewusstsein von dem wesentlich Neuen hatte, das damit aufgenommen werde. Man ist weiter gegangen und sogar genöthigt worden, zu der Wortsprache seine Zuflucht zu nehmen, da die Zeichensprache der Analysis versagte, wenn z. B. von einer Function die Rede war, deren Werth für rationale Argumente 1, für irrationale 0 ist.
Zweitens ist der Kreis dessen erweitert worden, was als Argument und Functionswerth auftreten kann, durch Aufnahme der complexen Zahlen. Hiermit musste zugleich der Sinn der Ausdrücke «Summe», «Product» u. s. w. weiter bestimmt werden.
In beiden Richtungen gehe ich nun weiter. Zunächst nehme ich zu den Zeichen +, – u. s. w., die zur Bildung eines Functionsausdruckes dienen, {13} noch hinzu Zeichen wie =, >, <, sodass ich z. B. von der Function x2 = 1 sprechen kann, wo x wie früher das Argument vertritt. Die erste Frage, die hier auftaucht, ist die nach den Werthen dieser Function für verschiedene Argumente. Setzen wir einmal der Reihe nach für x –1, 0, 1, 2, so erhalten wir
(–1)2 = 1,
02 = 1,
12 = 2,
22 = 1.
Von diesen Gleichungen sind die erste und dritte wahr, die anderen falsch. Ich sage nun: «der Werth unserer Function ist ein Wahrheitswerth» und unterscheide den Wahrheitswerth des Wahren von dem des Falschen. Den einen nenne ich kurz das Wahre, den andern das Falsche. Hiernach bedeutet z. B. «22 = 4» das Wahre ebenso, wie etwa «22» 4 bedeutet. Und es bedeutet «22 = 1» das Falsche. Demnach bedeuten
«22 = 4», «2 > 1», «24 = 42»
dasselbe, nämlich das Wahre, sodass wir in
(22 = 4) = (2 > 1)
eine richtige Gleichung haben.
Es liegt hier der Einwand nahe, dass «22 = 4» und «2 > 1» doch ganz Verschiedenes besagen, ganz verschiedene Gedanken ausdrücken; aber auch «24 = 42» und «4 · 4 = 42» drücken verschiedene Gedanken aus; und doch kann man «24» durch «4 · 4» ersetzen, weil beide Zeichen dieselbe Bedeutung haben. Folglich haben auch «24 = 42» und «4 · 4 = 42» dieselbe Bedeutung. Man sieht {14} hieraus, dass die Gleichheit der Bedeutung nicht die Gleichheit des Gedankens zur Folge hat. Wenn wir sagen «der Abendstern ist ein Planet, dessen Umlaufszeit kleiner ist als die der Erde», so haben wir einen anderen Gedanken ausgedrückt als in dem Satze «der Morgenstern ist ein Planet, dessen Umlaufszeit kleiner ist als die der Erde»; denn, wer nicht weiss, dass der Morgenstern der Abendstern ist, könnte den einen für wahr, den andern für falsch halten; und doch muss die Bedeutung beider Sätze dieselbe sein, weil nur die Wörter «Abendstern» und «Morgenstern» mit einander vertauscht sind, welche dieselbe Bedeutung haben, d. h. Eigennamen desselben Himmelskörpers sind. Man muss Sinn und Bedeutung unterscheiden. «24» und «4 · 4» haben zwar dieselbe Bedeutung; d. h. sie sind Eigennamen derselben Zahl; aber sie haben nicht denselben Sinn; und daher haben «24 = 42» und «4 · 4 = 42» zwar dieselbe Bedeutung, aber nicht denselben Sinn; d. h. in diesem Falle: sie enthalten nicht denselben Gedanken 6).
Mit demselben Rechte also, wie wir schreiben
«24 = 4 · 4»
können wir auch schreiben
«(24 = 42) = (4 · 4 = 42)»
und
»(22 = 4) = (2 > 1)». {15}
Ferner könnte gefragt werden, zu welchem Zwecke denn die Zeichen =, >, < in den Kreis derer aufgenommen werden, die einen Functionsausdruck bilden helfen. Es scheint jetzt die Meinung immer mehr Anhänger zu gewinnen, dass die Arithmetik weiter entwickelte Logik ist, dass eine strengere Begründung der arithmetischen Gesetze auf rein logische und nur auf solche zurückführt. Auch ich bin dieser Meinung und gründe darauf die Forderung, dass die arithmetische Zeichensprache zu einer logischen erweitert werden muss. Wie dies in unserem Falle geschieht, wird nun anzudeuten sein.
Wir sahen, dass der Werth unserer Function x2 = 1 immer einer der beiden Wahrheitswerthe ist. Wenn nun für ein bestimmtes Argument, z. B. –1, der Functionswerth das Wahre ist, so können wir das so ausdrücken: «die Zahl –1 hat die Eigenschaft, dass ihr Quadrat 1 ist», oder kürzer: «–1 ist eine Quadratwurzel aus 1», oder «–1 fällt unter den Begriff der Quadratwurzel aus 1». Wenn der Werth der Function x2 = 1 für ein Argument, z. B. 2, das Falsche ist, so werden wir das so ausdrücken können: «2 ist nicht Quadratwurzel aus 1» oder «2 fällt nicht unter den Begriff Quadratwurzel aus 1». Wir sehen daraus, wie eng das, was in der Logik Begriff genannt wird, zusammenhängt mit dem, was wir Function nennen. Ja, man wird geradezu sagen können: ein Begriff ist eine Function, deren Werth immer ein Wahrheitswerth ist. Auch der Werth der Function
(x + 1)2 =2(x + 1) {16}
ist immer ein Wahrheitswerth. Wir erhalten das Wahre z. B. für das Argument –1 und werden dies auch so aussprechen können: –1 ist eine Zahl, die um 1 kleiner ist als eine Zahl, deren Quadrat ihrem Zweifachen gleich ist. Hiermit ist das Fallen der Zahl –1 unter einen Begriff ausgedrückt. Nun haben die Functionen
x2 = 1 und (x + 1)2 = 2(x + 1)
für dasselbe Argument immer denselben Werth, nämlich für –1 und +1 das Wahre, für alle anderen Argumente das Falsche. Nach dem früher Festgestellten werden wir also sagen, dass diese Functionen denselben Werthverlauf haben, und dies so in Zeichen ausdrücken:
ἐ(ε2 = 1) = ἀ((α + 1)2 = 2(α + 1)).
In der Logik nennt man dies Gleichheit des Umfanges der Begriffe. Wir können demnach als Begriffsumfang den Werthverlauf einer Function bezeichnen, deren Werth für jedes Argument ein Wahrheitswerth ist.
Wir werden bei den Gleichungen und Ungleichungen nicht stehen bleiben. Die sprachliche Form der Gleichungen ist ein Behauptungssatz. Ein solcher enthält als Sinn einen Gedanken – oder macht wenigstens Anspruch darauf, einen zu enthalten –; und dieser Gedanke ist im Allgemeinen wahr oder falsch; d. h. er hat im Allgemeinen einen Wahrheitswerth, der ebenso als Bedeutung des Satzes aufzufassen ist, wie etwa die Zahl 4 die Bedeutung des Ausdruckes «2 + 2» ist, oder wie London die Bedeutung des Ausdruckes «Englands Hauptstadt» ist. {17}
Behauptungssätze im Allgemeinen kann man ebenso wie Gleichungen oder Ungleichungen oder analytische Ausdrücke zerlegt denken in zwei Theile, von denen der eine in sich abgeschlossen, der andere ergänzungsbedürftig, ungesättigt ist. So kann man z. B. den Satz
«Caesar eroberte Gallien»
zerlegen in «Caesar» und «eroberte Gallien». Der zweite Theil ist ungesättigt, führt eine leere Stelle mit sich , und erst dadurch , dass diese Stelle von einem Eigennamen ausgefüllt wird oder von einem Ausdrucke, der einen Eigennamen vertritt, kommt ein abgeschlossener Sinn zum Vorschein. Ich nenne auch hier die Bedeutung dieses ungesättigten Theiles Function. In diesem Falle ist das Argument Caesar.
Wir sehen, dass hier zugleich eine Erweiterung in der anderen Richtung vorgenommen ist, nämlich hinsichtlich dessen, was als Argument auftreten kann. Es sind nicht mehr blos Zahlen zuzulassen, sondern Gegenstände überhaupt, wobei ich allerdings auch Personen zu den Gegenständen rechnen muss. Als mögliche Functionswerthe sind schon vorhin die beiden Wahrheitswerthe eingeführt. Wir müssen weiter gehen und Gegenstände ohne Beschränkung als Functionswerthe zulassen. Um hierfür ein Beispiel zu haben, gehen wir etwa aus von dem Ausdrucke
«die Hauptstadt des deutschen Reichs».
Dieser vertritt offenbar einen Eigennamen und bedeutet einen Gegenstand. Zerlegen wir ihn nun in die Theile {18}
«die Hauptstadt des»
und
«deutsches Reich»,
wobei ich die Form des Genitivs zum ersten Theile rechne, so ist dieser ungesättigt, während der andere in sich abgeschlossen ist. Ich nenne also dem Früheren gemäss
«die Hauptstadt des x»
Ausdruck einer Function. Nehmen wir als ihr Argument das deutsche Reich, so erhalten wir als Functionswerth Berlin.
Wenn wir so Gegenstände ohne Einschränkung als Argumente und als Functionswerthe zugelassen haben, so fragt es sich nun, was hier Gegenstand genannt wird. Eine schulgemässe Definition halte ich für unmöglich, weil wir hier etwas haben, was wegen seiner Einfachheit eine logische Zerlegung nicht zulässt. Es ist nur möglich, auf das hinzudeuten, was gemeint ist. Hier kann nur kurz gesagt werden: Gegenstand ist Alles, was nicht Function ist, dessen Ausdruck also keine leere Stelle mit sich führt.
Ein Behauptungssatz enthält keine leere Stelle und darum ist seine Bedeutung als Gegenstand anzusehen. Diese Bedeutung aber ist ein Wahrheitswerth. Also sind die beiden Wahrheitswerthe Gegenstände.
Wir haben vorhin Gleichungen zwischen Werthverläufen aufgestellt, z. B.
«ἐ(ε2 – 4ε) = ἀ(α(α – 4))».
Wir können dies zerlegen in «ἐ(ε2 – 4ε)» und «() = ἀ(α(α – 4))».
Dieser letzte Theil ist ergänzungsbedürftig, indem er links vom Gleichheitszeichen eine leere {19} Stelle mit sich führt. Der erste Theil «ἐ(ε2 – 4ε)» ist völlig in sich abgeschlossen, bedeutet also einen Gegenstand. Werthverläufe von Functionen sind Gegenstände, während Functionen selbst es nicht sind. Wir hatten auch ἐ(ε2 = 1) Werthverlauf genannt, konnten es aber auch bezeichnen als Umfang des Begriffes Quadratwurzel aus 1. Auch Begriffsumfänge sind also Gegenstände, obwohl die Begriffe selbst es nicht sind.
Nachdem wir so den Umkreis dessen, was als Argument genommen werden darf, erweitert haben, müssen genauere Festsetzungen über die Bedeutungen der schon gebräuchlichen Zeichen getroffen werden. Solange man von den Gegenständen nur die ganzen Zahlen in der Arithmetik betrachtet, deuten die Buchstaben a und b in «a + b» nur ganze Zahlen an, braucht das Pluszeichen nur zwischen ganzen Zahlen erklärt zu werden. Jede Erweiterung des Umkreises der Gegenstände, die durch «a» und «b» angedeutet werden, nöthigt zu einer neuen Erklärung des Pluszeichens. Vorkehrungen zu treffen, dass nie ein Ausdruck bedeutungslos werden könne, dass man nie, ohne es zu merken, mit leeren Zeichen rechne in der Meinung, mit Gegenständen zu thun zu haben, erscheint als Gebot der wissenschaftlichen Strenge. Man hat früher mit divergenten unendlichen Reihen üble Erfahrungen gemacht. Es ist also nöthig, Festsetzungen zu machen, aus denen hervorgeht, was z. B.
«☼ + 1»
bedeutet, wenn «☼» die Sonne bedeuten soll. Wie diese Festsetzungen geschehen, ist verhältnissmässig {20} gleichgültig; wesentlich ist aber, dass sie gemacht werden, dass «a + b» immer eine Bedeutung erhalte, welche Zeichen bestimmter Gegenstände auch für «a» und «b» eingesetzt werden mögen. Für die Begriffe haben wir hierin die Forderung, dass sie für jedes Argument einen Wahrheitswerth als Werth haben, dass für jeden Gegenstand bestimmt sei, ob er unter den Begriff falle oder nicht; mit anderen Worten: wir haben für Begriffe die Forderung ihrer scharfen Begrenzung, ohne deren Erfüllung es unmöglich wäre, logische Gesetze von ihnen aufzustellen. Für jedes Argument x, für das «x + 1» bedeutungslos wäre, hätte auch die Function x + 1 = 10 keinen Werth, also auch keinen Wahrheitswerth, sodass der Begriff,
was um 1 vermehrt 10 ergiebt,
keine scharfe Grenze hätte. Die Forderung der scharfen Begrenzung der Begriffe zieht also die für Functionen im Allgemeinen nach sich, dass sie für jedes Argument einen Werth haben müssen. Wir haben die Wahrheitswerthe bisher nur als Functionswerthe, nicht als Argumente betrachtet. Nach dem eben Gesagten muss eine Function auch dann einen Werth erhalten, wenn als Argument ein Wahrheitswerth genommen wird; aber eine Festsetzung zu dem Zwecke mag bei den schon üblichen Zeichen meist nur geschehen, damit sie geschehe, ohne dass dabei sehr in Betracht kommt, was bestimmt wird. Es mögen nun aber einige Functionen betrachtet werden, an denen uns grade dann gelegen ist, wenn ihr Argument ein Wahrheitswerth ist. {21}
Ich führe als solche ein
──x,
indem ich festsetze, dass der Werth dieser Function das Wahre sein soll, wenn als Argument das Wahre genommen wird, dass hingegen in allen anderen Fällen der Werth dieser Function das Falsche ist; also sowohl dann, wenn das Argument das Falsche ist, als auch dann, wenn es kein Wahrheitswerth ist. Danach ist z. B.
──1 + 3 = 4
das Wahre, während sowohl
──1 + 3 = 5
als auch
──4
das Falsche ist. Diese Function hat also als Werth das Argument selbst, wenn dieses ein Wahrheitswerth ist. Ich habe diesen wagerechten Strich früher Inhaltsstrich genannt, ein Name, der nun nicht mehr passend scheint. Ich will ihn jetzt einfach den Wagerechten nennen.
Wenn man eine Gleichung oder Ungleichung hinschreibt, z. B. 5 > 4, so will man gewöhnlich damit zugleich ein Urtheil ausdrücken; man will in unserem Falle behaupten, 5 sei grösser als 4. Nach der von mir hier dargelegten Auffassung hat man in «5 > 4» oder «1 + 3 = 5» nur Ausdrücke von Wahrheitswerthen, ohne dass damit etwas behauptet werden soll. Diese Trennung des Urtheilens von dem, worüber geurtheilt wird, erscheint unumgänglich, weil sonst eine blosse Annahme, das Setzen eines Falles, ohne gleich über {22} sein Eintreten zu urtheilen, nicht ausdrückbar wäre. Wir bedürfen also eines besonderen Zeichens, um etwas behaupten zu können. Ich bediene mich hierzu eines senkrechten Striches am linken Ende des Wagerechten, sodass wir z. B. mit
«├──2 + 3 = 5»
behaupten: 2 + 3 ist gleich 5. Es wird also nicht blos wie in
«2 + 3 = 5»
ein Wahrheitswerth hingeschrieben, sondern zugleich auch gesagt, dass er das Wahre sei 7).
Die nächst einfache Function mag die sein, deren Werth gerade für die Argumente das Falsche ist, für welche der Werth von ──x das Wahre ist, und deren Werth umgekehrt für die Argumente das Wahre ist, für welche der Werth von ──x das Falsche ist. Ich bezeichne sie so
─┬─x,
wobei ich den kleinen senkrechten Strich Verneinungsstrich nenne. Ich fasse diese Function auf als eine Function mit dem Argumente ──x:
(─┬─x) = (─┬─ (──x)),
indem ich die beiden wagerechten Striche verschmolzen denke. Es ist aber auch
(── (─┬─x)) = (─┬─x), {23}
weil der Werth von ─┬─x immer ein Wahrheitswerth ist. Ich fasse also in «─┬─x» die beiden Strichtheile rechts und links vom Verneinungsstriche als Wagerechte auf in dem vorhin erklärten besonderen Sinne des Wortes. Es bedeutet demnach z. B.
«─┬─22 = 5»
das Wahre, und wir können den Urtheilsstrich anbringen:
├─┬─22 = 5;
und damit behaupten wir, dass 22 = 5 nicht das Wahre ist, oder dass 22 nicht 5 ist. Es ist aber auch
─┬─2
das Wahre, weil ──2 das Falsche ist:
├─┬─2;
d. h. 2 ist nicht das Wahre.
Wie ich die Allgemeinheit darstelle, wird an einem Beispiele am besten zu erkennen sein. Es solle ausgedrückt werden, dass jeder Gegenstand sich selbst gleich ist. Wir haben in
x = x
eine Function , deren Argument durch «x» angedeutet ist. Es soll nun gesagt werden, dass der Werth dieser Function immer das Wahre ist, was man auch als Argument nehmen möge. Ich verstehe nun unter
« f( f( )» )»
das Wahre, wenn die Function f(x) als Werth immer das Wahre hat, was auch ihr Argument sein möge; in allen anderen Fällen soll {24}
« f( f( )» )»
das Falsche bedeuten. Für unsere Function x = x haben wir nun den ersten Fall. Es ist also
  = = 
das Wahre; und wir schreiben dies so:
├  = = 
Die wagerechten Striche rechts und links von der Höhlung sind als Wagerechte in unserem Sinne aufzufassen. Statt « » könnte irgend ein anderer deutscher Buchstabe gewählt werden mit Ausnahme derjenigen, die wie » könnte irgend ein anderer deutscher Buchstabe gewählt werden mit Ausnahme derjenigen, die wie  , ,  als Functionsbuchstaben dienen sollen. als Functionsbuchstaben dienen sollen.
Diese Bezeichnungsart gewährt die Möglichkeit, die Allgemeinheit zu verneinen wie in
─┬─  2 = 1 2 = 1
Es ist nämlich   2 = 1 das Falsche, weil nicht für jedes Argument der Werth der Function x2 = 1 das Wahre ist. Wir erhalten nämlich z. B. für das Argument 2 22 = 1; das ist das Falsche. Ist nun 2 = 1 das Falsche, weil nicht für jedes Argument der Werth der Function x2 = 1 das Wahre ist. Wir erhalten nämlich z. B. für das Argument 2 22 = 1; das ist das Falsche. Ist nun   2 = 1 das Falsche, so ist ─┬─ 2 = 1 das Falsche, so ist ─┬─  2 = 1 das Wahre nach dem, was über den Verneinungsstrich oben festgestellt ist. Wir haben also 2 = 1 das Wahre nach dem, was über den Verneinungsstrich oben festgestellt ist. Wir haben also
├─┬─  2 = 1; 2 = 1;
d. h. «nicht jeder Gegenstand ist Quadratwurzel aus 1», oder «es giebt Gegenstände, die nicht Quadratwurzeln aus 1 sind».
Kann man auch ausdrücken, dass es Quadratwurzeln {25} aus 1 gebe? Gewiss! man braucht nur statt der Function x2 = 1 die Function
─┬─ x2 = 1
zu nehmen. Aus
« ─┬─ ─┬─  2 = 1» 2 = 1»
entsteht durch Verschmelzung der Wagerechten
« ─┬─ ─┬─  2 = 1» 2 = 1»
Dies bedeutet das Falsche, weil nicht für jedes Argument der Werth der Function
─┬─ x2 = 1
das Wahre ist. Es ist z. B.
─┬─ 12 = 1
das Falsche, weil 12 = 1 das Wahre ist. Da nun also
 ─┬─ ─┬─  2 = 1 2 = 1
das Falsche ist, so ist
─┬─ ─┬─ ─┬─  2 = 1 2 = 1
das Wahre:
├─┬─ ─┬─ ─┬─  2 = 1; 2 = 1;
d. h. «nicht für jedes Argument wird der Werth der Funktion
─┬─ x2 = 1
das Wahre», oder «nicht für jedes Argument wird der Werth der Function x2 = 1 das Falsche», oder «es giebt mindestens eine Quadratwurzel aus 1».
Es mögen hier noch einige Beispiele in Zeichen und Worten folgen:
├─┬─ ─┬─ ─┬─  ≥ 0 ≥ 0
es giebt mindestens eine positive Zahl; {26}
├─┬─ ─┬─ ─┬─  < 0 < 0
es giebt mindestens eine negative Zahl;
├─┬─ ─┬─ ─┬─  3 – 3 3 – 3 2 + 2 2 + 2 = 0 = 0
es giebt mindestens eine Wurzel der Gleichung
x3 – 3x2 + 2x = 0.
Hieraus ist zu sehen, wie die wichtigen Existentialsätze auszudrücken sind. Deuten wir einen Begriff unbestimmt mit dem Functionsbuchstaben f an, so haben wir in
─┬─ ─┬─ f ( ─┬─ f ( ) )
die Form, in der die letzten Beispiele, abgesehen vom Urtheilsstriche, enthalten sind. Die Ausdrücke
«─┬─ ─┬─ ─┬─  2 = 1», «─┬─ 2 = 1», «─┬─ ─┬─ ─┬─  > 0», «─┬─ > 0», «─┬─ ─┬─ ─┬─  2 < 0», 2 < 0»,
«─┬─ ─┬─ ─┬─  3 – 3 3 – 3 2 + 2 2 + 2 = 0» = 0»
gehen aus dieser Form in ähnlicher Weise hervor, wie z. B. aus x2 hervorgehen «12», «22», «32». Wie wir nun in x2 eine Function haben, deren Argument durch «x» angedeutet ist, so fasse ich auch
«─┬─ ─┬─ f ( ─┬─ f ( )» )»
als Ausdruck einer Function auf, deren Argument durch «f» angedeutet wird. Eine solche Function ist offenb[a]r grundverschieden von den bisher betrachteten; denn als ihr Argument kann nur eine Function auftreten. Wie nun Functionen von Gegenständen grundverschieden sind, so sind auch Functionen, deren Argumente Functionen sind und sein müssen, grundverschieden von Functionen, deren Argumente Gegenstände sind und nichts {27} Anderes sein können. Diese nenne ich Functionen erster, jene Functionen zweiter Stufe. Ebenso unterscheide ich Begriffe erster und zweiter Stufe 8). Functionen zweiter Stufe hat man eigentlich in der Analysis längst gehabt, z. B. in den bestimmten Integralen, sofern man die zu integrirende Function als Argument betrachtet.
Es mag noch etwas über Functionen mit zwei Argumenten hinzugefügt werden. Wir erhielten den Ausdruck einer Function, indem wir das zusammengesetzte Zeichen eines Gegenstandes zerlegten in einen gesättigten und einen ungesättigten Theil. Wir zerlegen so z. B. das Zeichen
«3 > 2»
des Wahren in «3» und «x > 2». Wir können den ungesättigten Theil «x > 2» weiter in derselben Weise zerlegen in «2» und
«x > y»
wo nun «y» die leere Stelle kenntlich macht, welche vorher durch «2» ausgefüllt war. Wir haben in
«x > y»
eine Function mit zwei Argumenten, deren eines durch «x», deren anderes durch «y» angedeutet ist, und in
3 > 2
haben wir den Werth dieser Function für die Argumente {28} 3 und 2. Wir haben hier eine Function, deren Werth stets ein Wahrheitswerth ist. Solche Functionen mit einem Argumente haben wir Begriffe genannt; solche mit zwei Argumenten nennen wir Beziehungen. Beziehungen haben wir z. B. auch in
x2 + y2 = 9
und in
x2 + y2 < 9,
während die Function
x2 + y2
als Werthe Zahlen hat. Wir werden sie also nicht Beziehung nennen.
Es mag hier eine nicht der Arithmetik eigenthümliche Function angeführt werden. Der Werth der Function

sei dann das Falsche, wenn als y-Argument das Wahre und zugleich als x-Argument ein Gegenstand genommen wird, der nicht das Wahre ist; in allen anderen Fällen sei der Werth dieser Function das Wahre. Der untere wagerechte Strich und die beiden Theile, in die der obere durch den senkrechten zerlegt wird, sind als Wagerechte aufzufassen. Demzufolge kann man als Argumente unserer Function immer ──x und ──y ansehen, d. h. Wahrheitswerthe.
Wir unterschieden unter den Functionen mit einem Argumente solche erster und zweiter Stufe. Hier ist eine grössere Mannigfaltigkeit möglich. Eine Function mit zwei Argumenten kann in Beziehung {29} auf diese von derselben oder von verschiedenen Stufen sein: gleichstufige, ungleichstufige Functionen. Die bisher betrachteten waren gleichstufige. Eine ungleichstufige Function ist z. B. der Differentialquotient, wenn als Argumente genommen werden die zu differenzirende Function und das Argument, für welches differenzirt wird, oder das bestimmte Integral, sofern als Argumente die zu integrirende Function und die obere Grenze genommen werden. Die gleichstufigen Functionen können wieder in solche erster und zweiter Stufe eingetheilt werden. Eine solche zweiter Stufe ist z. B.
F(f (1)),
wo «F» und «f» die Argumente andeuten.
Man muss bei den Functionen zweiter Stufe mit einem Argumente unterscheiden, je nachdem als dies Argument eine Function mit einem oder eine solche mit zwei Argumenten erscheinen kann; denn eine Function mit einem Argumente ist so wesentlich verschieden von einer solchen mit zwei Argumenten, dass die eine nicht an eben der Stelle als Argument auftreten kann, wo die andere es kann. Einige Functionen zweiter Stufe mit einem Argumente verlangen als solches eine Function mit einem Argumente, andere verlangen eine Function mit zwei Argumenten, und diese beiden Klassen sind scharf geschieden.
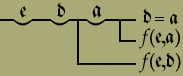
ist ein Beispiel einer Function zweiter Stufe mit {30} einem Argumente, die als solches eine Function mit zwei Argumenten verlangt. Der Buchstabe f deutet hierbei das Argument an, und die beiden durch das Komma getrennten Stellen in der auf «f» folgenden Klammer machen bemerklich, dass f eine Function mit zwei Argumenten vertritt.
Bei den Functionen mit zwei Argumenten wird die Mannigfaltigkeit noch grösser.
Wenn wir von hier auf die Entwickelung der Arithmetik zurückblicken, erkennen wir ein stufenweises Aufsteigen. Zuerst rechnete man mit einzelnen Zahlen, mit der 1, der 3 u. s. w.
2 + 3 = 5, 2 · 3 = 6
sind Lehrsätze dieser Art. Man schritt dann zu allgemeineren Gesetzen fort, die von allen Zahlen gelten. In der Bezeichnung entspricht dem der Uebergang zur Buchstabenrechnung. In
(a + b) · c = a · b + b · c
haben wir einen Lehrsatz dieser Art. Damit war man bei der Betrachtung einzelner Functionen angelangt, ohne noch das Wort im mathematischen Sinne zu gebrauchen und seine Bedeutung erfasst zu haben. Die nächst höhere Stufe war die Erkenntniss allgemeiner Gesetze von Functionen und damit die Prägung des Kunstausdruckes «Function». In der Bezeichnung entspricht dem die Einführung von Buchstaben wie f, F zur unbestimmten Andeutung von Functionen. In

haben wir einen Lehrsatz dieser Art. Damit hatte {31} man nun einzelne Functionen zweiter Stufe , ohne jedoch das zu erfassen, was wir Function zweiter Stufe genannt haben. Indem man dies thut, macht man den nächsten Fortschritt. Man könnte denken, dass dies so weiter ginge. Wahrscheinlich ist aber schon dieser letzte Schritt nicht so folgenreich wie die früheren, weil man statt der Functionen zweiter Stufe im weiteren Fortgang Functionen erster Stufe betrachten kann, wie an einem anderen Orte gezeigt werden soll. Damit ist aber der Unterschied zwischen Functionen erster und zweiter Stufe nicht aus der Welt geschafft, weil er nicht willkürlich gemacht, sondern in der Natur der Sache tief begründet ist.
Man kann auch statt der Functionen mit zwei Argumenten Functionen eines einzigen, aber komplexen Arguments betrachten, wobei jedoch der Unterschied zwischen den Functionen mit einem und denen mit zwei Argumenten in ganzer Schärfe bestehen bleibt.
―――――――
1) Am 10. Januar 1879 und am 27. Januar 1882.
2) Die Grundlagen der Arithmetik, Breslau 1884, § 92 u. ff., und Sitzungsberichte der Jenaischen Gesellschaft für Medicin und Naturwissenschaft, Jahrg. 1885, Sitzung vom 17. Juli.
3) Vergleiche die Aufsätze: Zählen und Messen erkenntnisstheoretisch betrachtet von H. v. Helmholtz, und Ueber den Zahlbegriff von Leopold Kronecker. (Philosophische Aufsätze. Eduard Zeller zu seinem fünfzigjährigen Doctorjubiläum gewidmet. Leipzig 1887.)
4) Es handelt sich dabei immer darum, mit einem Zeichen einen Sinn oder eine Bedeutung zu verbinden. Wo Sinn und Bedeutung ganz fehlen, kann eigentlich weder von einem Zeichen, noch von einer Definition die Rede sein.
5) In manchen Wendungen der üblichen mathematischen Ausdrucksweise entspricht wohl das Wort «Function» dem, was ich hier Werthverlauf einer Function genannt habe. Aber Function in dem hier gebrauchten Sinne des Wortes ist das logisch Frühere.
6) Ich verkenne nicht, dass diese Wendung zunächst willkürlich und künstlich erscheinen mag, und dass eine eingehendere Begründung gefordert werden könnte. Man vergl. meinen nächstens erscheinenden Aufsatz über Sinn und Bedeutung in der Zeitschrift für Philosophie und phil. Kritik.
7) Der Urtheilsstrich kann nicht zur Bildung eines Functionsausdrucks gebraucht werden, weil er nicht mit anderen Zeichen zusammen zur Bezeichnung eines Gegenstandes dient. «├─2 + 3 = 5» bezeichnet nichts, sondern behauptet etwas.
8) Vergl. meine Grundlagen der Arithmetik (Breslau 1884) § 53 am Ende, wo ich statt «zweiter Stufe» «zweiter Ordnung» gesagt habe. Der ontologische Beweis für das Dasein Gottes leidet an dem Fehler, dass er die Existenz wie einen Begriff erster Stufe behandelt.
|