| |
Bertrand Russell an Gottlob Frege
Friday's Hill.
Haslemere.
Den 16 Juni 1902
Sehr geehrter Herr College!
Seit anderthalb Jahren kenne ich Ihre «Grundgesetze der Arithmetik», aber jetzt erst ist es mir möglich geworden die Zeit zu finden für das gründliche Studium das ich Ihren Schriften zu widmen beabsichtige. Ich finde mich in allen Hauptsachen mit Ihnen in vollem Einklang, besonders in der Verwerfung jedes psychologischen Moments von der Logik, und in der Schätzung einer Begriffsschrift für die Grundlagen der Mathematik und der formalen Logik, welche übrigens kaum zu unterscheiden sind. In vielen einzelnen Fragen finde ich bei Ihnen Discussionen, Unterscheidungen, und Definitionen, die man vergebens bei anderen Logikern sucht. Besonders über die Funktion (§ 9 Ihrer Begriffsschrift) bin ich bis ins Einzelne selbständig zu denselben Ansichten geführt worden. Nur in einem Punkte ist mir eine Schwierigkeit begegnet. Sie behaupten (S. 17) es könne auch die Funktion das unbestimmte Element bilden. Dies habe ich früher geglaubt, jedoch jetzt scheint mir diese Ansicht zweifelhaft, wegen des folgenden Widerspruchs: Sei w das Prädicat, ein Prädicat zu sein welches von sich selbst nicht prädicirt werden kann. Kann man w von sich selbst prädiciren? Aus jeder Antwort folgt das Gegentheil. Deshalb muss man schließen dass w kein Prädicat ist. Ebenso giebt es keine Klasse (als Ganzes) derjenigen Klassen die als Ganze sich selber nicht angehören. Daraus schliesse ich dass unter gewissen Umständen eine definierbare Menge kein Ganzes bildet.
Ich bin im Begriff ein Buch über die Prinzipien der Mathematik zu vollenden, und ich möchte darin Ihr Werk sehr ausführlich besprechen. Ihre Bücher habe ich schon, oder ich kaufe sie bald; aber ich wäre Ihnen sehr dankbar wenn Sie mir Sonderabdrücke Ihrer Artikel in verschiedenen Zeitschriften schicken könnten. Falls dies aber unmöglich sein sollte, so schaffe ich sie mir aus einer Bibliothek.
Die exacte Behandlung der Logik, in den Fundamentalfragen, wo die Symbolen versagen, ist sehr zurückgeblieben; bei Ihnen finde ich das Beste, was ich aus unserer Zeit kenne, und deshalb habe ich mir erlaubt, Ihnen mein tiefes Respekt auszudrücken. Es ist sehr zu bedauern, dass Sie nicht dazu gelangt sind, den zweiten Band Ihrer Grundgesetze zu veröffentlichen; hoffentlich wird das doch noch geschehen.
Mit hochachtungsvollem Grusse,
Ihr ergebenster
Bertrand Russell.
Obiger Widerspruch drückt sich in Peano's Begriffsschrift wie folgt aus:
w = cls ∩ xэ (x ~ εx) . 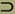 : wεw . = . w ~ εw . : wεw . = . w ~ εw .
Ich habe darüber an Peano geschrieben, aber er bleibt mir eine Antwort schuldig.
―――――
Gottlob Frege an Bertrand Russell
Jena, den 22. Juni 1902.
Sehr geehrter Herr College!
Besten Dank für Ihren interessanten Brief vom 16. Juni! Ich freue mich dass Sie in Vielem mit mir einverstanden sind, und dass Sie die Absicht haben, mein Werk ausführlich zu besprechen. Auf Ihren Wunsch sende ich Ihnen die folgenden Drucksachen
1. Kritische Beleuchtung etc.
2. Ueber die Begriffschrift des Herrn Peano etc.
3. Ueber Begriff und Gegenstand,
4. Ueber Sinn und Bedeutung,
5. Ueber formale Theorien der Arithmetik.
Ich habe einen leeren Umschlag erhalten, dessen Aufschrift von Ihrer Hand zu sein scheint. Ich vermuthe, dass Sie die Absicht gehabt haben, mir etwas zu schicken, was durch einen Zufall verloren gegangen ist. Ist dies der Fall, so danke ich Ihnen für die liebenswürdige Absicht. Die Vorderseite des Umschlags lege ich bei.
Wenn ich meine Begriffsschrift jetzt wieder lese, finde ich, dass ich in manchen Punkten anderer Ansicht geworden bin, wie Sie aus einer Vergleichung mit meinen Grundgesetzen d. A. ersehen werden. Den mit «Nicht minder erkennt man» beginnenden Absatz auf S. 7 meiner Begriffsschrift bitte ich zu streichen, da er fehlerhaft ist, was übrigens ohne nachtheilige Folgen für den übrigen Inhalt des Büchleins geblieben ist.
Ihre Entdeckung des Widerspruchs hat mich auf's Höchste überrascht und, fast möchte ich sagen, bestürzt, weil dadurch der Grund, auf dem ich die Arithmetik sich aufzubauen dachte, in's Wanken geräth. Es scheint danach, dass die Umwandlung der Allgemeinheit einer Gleichheit in eine Werthverlaufsgleichheit (§ 9 meiner Grundgesetze) nicht immer erlaubt ist, dass mein Gesetz V (§ 20. S. 36) falsch ist und dass meine Ausführungen im § 31 nicht genügen, in allen Fällen meinen Zeichenverbindungen eine Bedeutung zu sichern. Ich muss noch weiter über die Sache nachdenken. Sie ist um so ernster, als mit dem Wegfall meines Gesetzes V nicht nur die Grundlage meiner Arithmetik, sondern die einzig mögliche Grundlage der Arithmetik überhaupt zu versinken scheint. Und doch, sollte ich denken, muss es möglich sein, solche Bedingungen für die Umwandlung der Allgemeinheit einer Gleichheit in eine Werthverlaufsgleichheit aufzustellen, dass das Wesentliche meiner Beweise erhalten bleibt. Jedenfalls ist Ihre Entdeckung sehr merkwürdig und wird vielleicht einen grossen Fortschritt in der Logik zur Folge haben, so unerwünscht sie auf den ersten Blick auch scheint.
Uebrigens scheint mir der Ausdruck «Ein Praedicat wird von sich selbst praedicirt» nicht genau zu sein. Ein Praedicat ist in der Regel eine Function erster Stufe, die als Argument einen Gegenstand verlangt und also nicht sich selbst als Argument (Subject) haben kann. Ich möchte also lieber sagen: «Ein Begriff wird von seinem eigenen Umfange praedicirt». Wenn die Function Φ(ξ) ein Begriff ist, so bezeichne ich dessen Umfang (oder die zugehörige Klasse) durch «ἐΦ(ε)» (die Berechtigung hierzu ist mir nun freilich zweifelhaft geworden). In «Φ(ἐΦ(ε))» oder «ἐΦ(ε) ∩ ἐΦ(ε)» haben wir dann die Praedicirung des Begriffes Φ(ξ) von seinem eigenen Umfange.
Der zweite Band meiner Grundgesetze soll demnächst erscheinen. Ich werde ihm wohl einen Anhang geben müssen, in dem Ihre Entdeckung gewürdigt wird. Wenn ich nur erst den richtigen Gesichtspunkt dafür hätte!
Mit hochachtungsvollem Grusse
Ihr ergebenster
G. Frege.
―――――

Seite 2 von Freges Brief an Bertrand Russell
|
