| |
|
- D i s s e r t a t i o
1 7 9 9
Versio digitalis:
Frank Balbach
- __________________________________________
-
DEMONSTRATIO NOVA
THEOREMATIS
OMNEM FVNCTIONEM
ALGEBRAICAM
RATIONALEM INTEGRAM
VNIVS VARIABILIS
IN
FACTORES REALES PRIMI VEL SECUNDI GRADVS
RESOLVI POSSE
AVCTORE
CAROLO FRIDERICO GAVSS
HELMSTADII
APVD C. G. FLECKEISEN. 1799
1.
Quaelibet aequatio algebraica determinata reduci potest ad formam
xm+Axm-1+Bxm-2+ etc. +M=0,
ita vt m sit numerus integer positiuus. Si partem primam huius
aequationis per X denotamus, aequationique X=0 per plures
valores inaequales ipsius x satisfieri supponimus, puta ponendo
x=α, x=β, x=γ etc. functio X per productum e
factoribus x-α, x-β, x-γ etc. diuisibilis erit. Vice
versa, si productum e pluribus factoribus simplicibus x-α,
x-β, x-γ etc. functionem X metitur: aequationi
X=0 satisfiet, aequando ipsam x cuicunque quantitatum α,
β, γ etc. Denique si X producto ex m factoribus talibus
simplicibus aequalis est (siue omnes diuersi sint, siue quidam ex ipsis
identici): alii factores simplices praeter hos functionem X metiri non
poterunt. Quamobrem aequatio mti gradus plures quam
m radices habere nequit; simul vero patet, aequationem
mti gradus pauciores radices habere posse, etsi
X in m factores simplices resolubilis sit: si enim inter hos
factores aliqui sunt identici, multitudo modorum diuersorum aequationi
satisfaciendi necessario minor erit quam m. Attamen concinnitatis
caussa geometrae dicere maluerunt, aequationem in hoc quoque casu m
radices habere, et tantummodo quasdam ex ipsis aequales inter se euadere: quod
vtique sibi permittere potuerunt.
2.
Quae hucusque sunt enarrata, in libris algebraicis sufficienter demonstrantur
neque rigorem geometricum vspiam offendunt. Sed nimis praepropere et sine
praeuia demonstratione solida adoptauisse videntur analystae theorema cui tota
fere doctrina aequationum superstructa est: Quamuis functionem talem vt
X semper in m factores simplices resolui posse, siue hoc
quod cum illo prorsus conspirat, quamuis aequationem mti
gradus reuera habere m radices. Quum iam in aequationibus secundi
gradus saepissime ad tales casus perueniatur, qui theoremati huic repugnant:
algebraistae, vt hos illi subiicerent, coacti fuerunt, fingere quantitatem
quandam imaginariam cuius quadratum sit -1, et tum agnouerunt, si quantitates
formae a+b√-1 perinde concedantur vt reales, theorema non modo pro
aequationibus secundi gradus verum esse, sed etiam pro cubicis et biquadraticis.
Hinc vero neutiquam inferre licuit, admissis quantitatibus formae
a+b√-1 cuiuis aequationi quinti superiorisue gradus satisfieri posse,
aut vti plerumque exprimitur (quamquam phrasim lubricam minus probarem) radices
cuiusuis aequationis ad formam a+b√-1 reduci posse. Hoc theorema ab eo,
quod in titulo huius scripti enunciatum est, nihil differt, si ad rem ipsam
spectas, huiusque demonstrationem nouam rigorosam tradere, constituit propositum
praesentis dissertationis.
Ceterum ex eo tempore, quo analystae comperti sunt, infinite multas
aequationes esse, quae nullam omnino radicem haberent, nisi quantitates formae
a+b√-1 admittantur, tales quantitates fictiae tamquam peculiare
quantitatum genus, quas imaginarias dixerunt, vt a realibus
distinguerentur, consideratae et in totam analysin introductae sunt; quonam
iure? hoc loco non disputo. – Demonstrationem meam absque omni quantitatum
imaginarium subsidio absoluam, etsi eadem libertate, qua omnes recentiores
analystae vsi sunt, etiam mihi vti liceret.
3.
Quamuis ea, quae in plerisque libris elementaribus tamquam demonstratio
theorematis nostri afferuntur, tam leuia sint, tantumque a rigore geometrico
abhorreant, vt vix mentione sint digna tamen, ne quid deesse videatur, paucis
illa attingam. «Vt demonstrent, quamuis aequationem
xm+Axm-1+Bxm-2 + etc.
+M=0, siue X=0, reuera habere m radices, suscipiunt
probare, X in m factores simplices resolui posse. Ad hunc
finem assumunt m factores simplices x-α, x-β,
x-γ etc. vbi α, β, γ etc. adhuc sunt incognitae, productumque
ex illis aequale ponunt functioni X. Tum ex comparatione coëfficientium
deducunt m aequationes, ex quibus incognitas α, β, γ etc.
determinari posse aiunt, quippe quarum multitudo etiam sit m. Scilicet
m-1 incognitas eliminari posse, vnde emergere aequationem, quae, quam
placuerit, incognitam solam contineat.» Vt de reliquis, quae in tali
argumentatione reprehendi possent, taceam, quaeram tantummodo, vnde certi esse
possimus, vltimam aequationem reuera vllam radicem habere? Quidni fieri posset,
vt neque huic vltimae aequationi neque propositae, vlla magnitudo in toto
quantitatum realium atque imaginariarum ambitu satisfaciat? – Ceterum periti
facile perspicient, hanc vltimam aequationem necessario cum proposita omnino
identicam fore, siquidem calculus rite fuerit institutus; scilicet
eliminatis incognitis β, γ etc. aequationem
αm+Aαm-1+Bαm-2+ etc. +M=0
prodire debere. Plura de isto ratiocinio exponere necesse non est.
Quidam auctores, qui debilitatem huius methodi percepisse videntur, tamquam
axioma assumunt, quamuis aequationem reuera habere radicos, si non
possibiles, impossibiles. Quid sub quantitatibus possibilibus et impossibilibus
intellegi velint, haud satis distincte exposuisse videntur. Si quantitates
possibiles idem denotare debent vt reales, impossibiles idem vt imaginariae:
axioma illud neutiquam admitti potest, sed necessario demonstratione opus habet.
Attamen in illo sensu expressiones accipiendae non videntur, sed axiomatis mens
haec potius videtur esse: «Quamquam nondum sumus certi, necessario dari
m quantitates reales vel imaginarias, quae alicui aequationi datae
mti gradus satisfaciant, tamen aliquantisper hoc supponemus;
nam si forte contingeret, vt tot quantitates reales et imaginariae inueniri
nequeant, certe effugium patebit, vt dicamus reliquas esse impossibiles.»
Si quis hac phrasi vti mauult quam simpliciter dicere, aequationem in hoc casu
tot radices non habituram, a me nihil obstat: at si tum his radicibus
impossibilibus ita vtitur tamquam aliquid veri sint, et e. g. dicit, summam
omnium radicum aequationis xm+Axm-1+ etc.
=0, esse =-A, etiamsi impossibiles inter illas sint (quae
expressio proprie significat, etiamsi aliquae deficiant): hoc neutiquam
probare possum. Nam radices impossibiles, in tali sensu acceptae, tamen sunt
radices, et tum axioma illud nullo modo sine demonstratione admitti potest,
neque inepte dubitares, annon aequationes exstare possint, quae ne impossibiles
quidem radices habeant? *1)
4.
Antequam aliorum geometrarum demonstrationes theorematis nostri recenseam, et
quae in singulis reprehenda mihi videantur, exponam: obseruo sufficere si
tantummodo ostendatur, omni aequationi quantiuis gradus
xm+Axm-1+Bxm-2+ etc. +M=0
siue X=0 (vbi coëfficientes A, B etc. reales esse supponuntur)
ad minimum vno modo satisfieri posse per valorem ipsius x sub forma
a+b√-1 contentum. Constat enim, X tunc diuisibilem fore per
factorem realem secundi gradus xx-2ax+aa+bb, si b non fuerit
=0, et per factorem realem simplicem x-a, si b=0. In
vtroque casu quotiens erit realis, et inferioris gradus quam X; et quum
hic eadem ratione factorem realem primi secundiue gradus habere debeat, patet,
per continuationem huius operationis functionem X tandem in factores
reales simplices vel duplices resolutum iri, aut, si pro singulis factoribus
realibus duplicibus binos imaginarios simplices adhibere mauis, in m
factores simplices.
5.
Prima theorematis demonstratio illustri geometrae
d'Alembert debetur, Recherches sur le calcul intégral, Histoire de l'Acad. de
Berlin, Année 1746, p. 182. sqq. Eadem extat in Bongainville, Traité du
calcul intégral, à Paris 1754. p. 47. sqq. Methodi huius praecipua momenta
haec sunt.
Primo ostendit, si functio quaecunque X quantitatis variabilis
x fiat =0 aut pro x=0 aut pro x=∞, atque
valorem infinite paruum realem positiuum nancisci possit tribuendo ipsi
x valorem realem: hanc functionem etiam valorem infinite paruum realem
negatiuum obtinere posse per valorem ipsius x vel realem vel sub forma
imaginaria p+q√-1 contentum. Scilicet designante Ω valorem
infinite paruum ipsius X, et ω valorem respondentem ipsius
x, asserit ω per seriem valde conuergentem
aΩα+bΩβ+cΩγ etc. exprimi posse, vbi
exponentes α, β, γ etc. sint quantitates rationales continuo
crescentes, et quae adeo ad minimum in distantia certa ab initio positiuae
euadant, terminosque, in quibus adsint, infinite paruos reddant. Iam si inter
omnes hos exponentes nullus occurat, qui sit fractio denominatoris paris, omnes
terminos seriei reales fieri tum pro positiuo tum pro negatiuo valore ipsius
Ω; si vero quaedam fractiones denominatoris paris inter illos
exponentes repariantur, constare, pro valore negatiuo ipsius Ω terminos
respondentes in forma p+q√-1 contentos esse. Sed propter infinitam
seriei conuergentiam in casu priori sufficere, si terminus primus (i. e.
maximus) solus retineatur, in posteriori vltra eum terminum, qui partem
imaginariam primus producat, progredi opus non esse.
Per simila ratiocinia ostendi posse, si X valorem realem negatiuum
infinite paruum ex valore reali ipsius x assequi possit: functionem
illam valorem realem positiuum infinite paruum ex valore reali ipsius x
vel ex imaginario sub forma p+q√-1 contento adipisci posse.
Hinc secundo concludit, etiam valorem aliquem realem finitum ipsius
X dari, in casu priori negatiuum, in posteriori positiuum, qui ex
valore imaginario ipsius x sub forma p+q√-1 contento produci
possit.
Hinc sequitur, si X sit talis functio ipsius x, quae
valorem realem V ex valore ipsius x reali v obtineat,
atque etiam valorem realem quantitate infinite parua vel maiorem vel minorem ex
valore reali ipsius x assequatur, eandem etiam valorem realem
quantitate infinite parua atque adeo finite vel minorem vel maiorem quam
V (resp.)recipere posse, tribuendo ipsi x valorem sub forma
p+q√-1 contentum. Hoc nullo negotio ex praecc. deriuatur, si pro
X substitui concipitur V+Y, et pro x, v+y.
Tandem affirmat ill. d'Alembert, si X totum interuallum aliquod
inter duos valores reales R, S percurrere posse supponatur ( i. e.
tum ipsi R, tum ipsi S, tum omnibus valoribus realibus
intermediis aequalis fieri), tribuendo ipsi x valores semper in forma
p+q√-1 contentos; functionem X quauis quantitate finita reali
adhuc augeri vel diminui posse (prout S>R vel S<R),
manente x semper sub forma p+q√-1. Si enim quantitas realis
U daretur (inter quam et R supponitur S iacere), cui
X per talem valorem ipsius x aequalis fieri non posset,
necessario valorem maximum ipsius X dari (scilicet quando
S>R; minimum vero, quando S<R), puta T, quem ex
valore ipsius x, p+q√-1, consequeretur, ita vt ipsi x
nullus valor sub simili forma contentus tribui posset, qui functionem X
vel minimo excessu propius versus U promoueret. Iam si in aequatione
inter X et x pro x vbique substituatur
p+q√-1, atque tum pars realis, tum pars, quae factorem √-1
implicet, hoc omisso, cifrae aequentur: ex duabus aequationibus hinc
prodeuntibus (in quibus p, q et X cum constantibus permixtae
occurrent) per eliminationem duas alias elici posse, in quarum altera p,
X et constantes reperiantur altera a p libera solas q, X
et constantes inuoluat. Quamobrem quum X per valores reales ipsarum
p,q omnes valores ab R vsque ad T percurrerit, per
praecc. X versus valorem U adhuc propius accedere posse
tribuendo ipsius p, q valores tales α+γ√-1, β+δ√-1
resp. Hinc vero fieri x=α-δ+(γ+β)√-1, i. e. adhuc sub forma
p+q√-1 esse, contra hyp.
Iam si X functionem talem vt
xm+Axm-1+Bxm-2 + etc.
+M denotare supponitur, nullo negotio perspicitur, ipsi x
tales valores reales tribui posse, vt X totum aliquod interuallum inter
duos valores reales percurrat. Quare x valorem aliquem sub forma
p+q√-1 contentum talem etiam nancisci poterit, vnde X fiat
=0. Q. E. D. *2)
6.
Quae contra demonstrationem d'Alembertianam obiici posse
videntur, ad haec fere redeunt.
1. Ill. d'A. nullum dubium mouet de existentia valorum ipsius
x quibus valores dati ipsius X respondeant, sed illam
supponit, solamque formam istorum valorum inuestigat.
Quamuis vero haec obiecto per se grauissima sit, tamen hic ad solam dictionis
formam pertinet, quae facile ita corrigi potest, vt illa penitus destruatur.
2. Assertio, ω per talem seriem qualem ponit semper exprimi posse,
certo est falsa, si X etiam funcionem quamlibet transscendentem
designare debet (vti d'A. pluribus locis innuit). Hoc e. g. manifestum
est, si ponitur X=e1/x, siue x=1/log X. Attamen si
demonstrationem ad eum casum restringimus, vbi X est functio algebraica
ipsius x (quod in praesenti negotio sufficit), propositio vtique est
vera. – Ceterum d'A. nihil pro confirmatione suppositionis suae attulit; cel.
Bougainville supponit X esse functionem algebraicam ipsius x,
et ad inuentionem seriei parallelogrammum Newtonianum commendat.
3. Quantitatibus infinite paruis liberius vtitur, quam cum geometrico rigore
consistere potest aut saltem nostra aetate (vbi illae merito male audiunt) ab
analysta scrupuloso concederetur, neque etiam saltum a valore infinite paruo
ipsius Ω ad finitum satis luculenter explicauit. Propositionem suam,
Ω etiam valorem aliquem finitum consequi posse, non tam ex
possibilitate valoris infinite parui ipsius Ω, concludere videtur quam
inde potius, quod denotante Ω quantitatem valde paruam, propter magnam
seriei conuergentiam, quo plures termini seriei accipiantur, eo propius ad
valorem verum ipsius ω accedatur, aut, quo plurium partium summa pro
ω accipiatur, eo exactius aequtioni, quae relationem inter ω
et Ω siue x et X exhibeat, satisfactum iri. Praeterea
quod tota haec argumentatio nimis vaga videtur, quam vt ulla conclusio rigorosa
inde colligi possit: obseruo, vtique dari series, quae quantumuis paruus valor
quantitati, secundum cuius potestates progrediuntur, tribuatur, nihilominus
semper diuergant, ita vt si modo satis longe continuentur, ad terminos quauis
quantitate data maiores peruenire possis. *3) Hoc euenit,
quando coëfficientes seriei progressionem hypergeometricam constituunt.
Quamobrem necessario demonstrari debuisset, talem seriem hypergeometricam in
casu praesenti prouenire non posse.
Ceterum mihi videtur, ill. d'A. hic non recte ad series infinitas confugisse,
hasque ad stabiliendum theorema hoc fundamentale doctrinae aequationum haud
idoneas esse.
4. Ex suppositione, X obtinere posse valorem S neque vero
valorem U, nondum sequitur, inter S et U necessario
valorem T iacere, quem X attingere sed non superare possit.
Superest adhuc alius casus: scilicet fieri posset, vt inter S et
U limes situs sit, ad quem accedere quidem quam prope velis possit
X, ipsum vero nihilominus numquam attingere. Ex argumentis ab ill. d'A.
allatis tantummodo sequitur, X omnem valorem, quem attigerit, adhuc
quantitate finita superare posse, puta quando enaserit =S, adhuc
quantitate aliqua finita Ω augeri posse; quo facto, nouum incrementum
Ω′ accedere, tunc iterum augmentum Ω′′ etc., ita vt quotcunque
incrementa iam adiecta sint, nullum pro vltimo haberi debeat, sed semper aliquod
nouum accedere possit. At quamuis multitudo incrementorum possibilium
nullis limitibus sit circumscripta: tamen vtique fieri posset, vt si incrementa
Ω, Ω′, Ω′′ etc. continuo decrescerent, nihilominus summa
S+Ω+Ω′+Ω′′ etc. limitem aliquem numquam attingeret, quotcunque termini
considerentur.
Quamquam hic casus occurrere non potest, quando X designat
functionem algebraicam integram ipsius x: tamen sine demonstratione,
hoc fieri non posse, methodus necessario pro incompleta habenda est. Quando vero
X est functio transscendens, siue etiam algebraica fracta, casus ille
vtique locum habere potest, e. g. semper quando valori cuidam ipsius
X valor infinite magnus ipsius x respondet. Tum methodus
d'Alembertiana non sine multis ambagibus, et in quibusdam casibus nullo forsan
modo, ad principia indubitata reduci posse videtur.
Propter has rationes demonstrationem d'Alembertianam pro satisfaciente habere
nequeo. Attamen hoc non obstante verus demonstrationis neruus probandi per omnes
obiectiones neutiquam infringi mihi videtur, credoque eidem fundamento (quamuis
longe diuersa ratione, et saltem maiori circumspicienta) non solum
demonstrationem rigorosam theorematis nostri superstrui, sed ibinde omnia peti
posse, quae circa aequationum transscendentium theoriam desiderari
queant. De qua re grauissima alia occasione fusius agam; conf. interim infra
art. 23.
7.
Post d'Alembertum ill. Euler disquisitiones suas de eodem argumento
promulgauit, Recherches sur les racines imaginaires des équations, Hist. de
l'Acad. de Berlin A. 1749. p. 223 sqq. Methodum duplicem hic tradidit:
prioris summa continetur in sequentibus.
Primo ill. E. suscipit demonstrare, si m denotet quamcunque
dignitatem numeri 2, functionem
x2m+Bx2x-2+Cx2m-3 + etc.
+M=X (in qua coëfficiens termini secundi est =0) semper in
duos factores reales resolui posse, in quibus x vsque ad m
dimensiones ascendat. Ad hunc finem duos factores assumit,
xm-uxm-1+α xm-2+β xm-3+
etc., et xm+ uxm-1+λ xm-2+μ
xm-3 etc. vbi coëfficientes u,α, β etc. λ, μ
etc. adhuc incogniti sunt, horumque productum aequale ponit functioni
X. Tum coëfficientium comparatio suppeditat 2m-1 aequationes,
manifestoque demonstrari tantummodo debet, incognitis u,α,β etc. λ,
μ etc. (quarum multitudo etiam est 2-1) tales valores reales
tribui posse, qui aequationibus illis satisfaciant. Iam E. affirmat, si primo
u tamquam cognita consideretur, ita vt multitudo incognitarum vnitate
minor sit quam multitudo aequationum, his secundum methodos algebraicas notas
rite combinatis omnes α, β etc. λ, μ etc. rationaliter et sine
vlla radicum extractione per u et coëfficientes B, C etc.
determinari posse, adeoque valores reales nancisci, simulac u realis
fiat. Praeterea vero omnes α, β etc. λ, μ etc. eliminari
poterunt, ita vt prodeat aequatio U=0, vbi U erit functio
integra solius u et coëfficientium cognitorum. Hanc aequationem ipsam
per methodum eliminationis vulgarem euoluere, opus immensum fore, quando
aequatio proposita X=0 est gradus aliquantum alti; et pro gradu
indeterminato, plane impossibile (iudice ipso E. p. 239.). Attamen sufficit,
vnam illius aequationis proprietatem nouisse, scilicet quod terminus vltimus in
U (qui incognitam u non implicat) necessario est negatiuus,
vnde sequi constat, aequationem ad minimum vnum radicem realem habere, siue
u et proin etiam α, β etc. λ, μ etc. ad minimum vno
modo realiter determinari posse: illam vero proprietatem per sequentes
reflexiones confirmare licet. Quum xm-uxm-1+α
xm-2+ etc. supponatur esse factor functionis X:
necessario u erit summa m radicum aequationis X=0,
adeoque totidem valores habere debebit, quot modis diuersis ex 2m
radicibus m excerpi possunt, siue per principia calculi combinationum
(2m . 2m-1 . ... . m+1) / (1 . 2 . 3 ... m) valores. Hic numerus semper
erit impariter par (demonstrationem haud difficilem supprimo): si itaque ponitur
=2k, ipsius semissis k impar erit; aequatio U=0 vero
erit gradus 2kti. Iam quoniam in aequatione X=0
terminus secundus deest: summa omnium 2m radicum erit 0; vnde
patet, si summa quarumcunque m radicum fuerit +p, reliquarum
summam fore -p, i. e. si +p est inter valores ipsius
u, etiam -p inter eosdem erit. Hinc E. concludit, U
esse productum ex k factoribus duplicibus talibus uu-pp,
uu-qq, vu-rr etc., denotantibus +p, -p, +q,
-q etc. omnes 2k radices aequationis U=0, vnde,
propter multitudinem imparem horum factorum, terminus vltimus in U erit
quadratum producti pqr etc. signo negatiuo affectum. Productum autem
pqr etc. semper ex coëfficientibus B, C etc. rationaliter
determinari potest, adeoque necessario erit quantitas realis. Huius itaque
quadratum signo negatiuo affectum certo erit quantitas negatiua. Q. E. D.
Quum hi duo factores reales ipsius X sint gradus
mti atque m potestas numeri 2: eadem ratione
vterque rursus in duos factores reales 1/2m dimensionum resolui
poterit. Quoniam vero per repetitam dimidiationem numeri m necessario
tandem ad binarium peruenitur, manifestum est, per continuationem operationis
functionem X tandem in factores reales secundi gradus resolutam haberi.
Quodsi vero functio talis proponitur, in qua terminus secundus non deest,
puta x2m+Ax2m-1+Bx2m-2+etc.
+M, designante etiamnum 2m potestatem binariam, haec per
substitutionem x=y-A/(2m) transibit in similem functionem termino
secundo carentem. Vnde facile concluditur, etiam illam functionem in factores
reales secundi gradus resolubilem esse.
Denique proposita functione gradus nti, designante
n numerum, qui non est potestas binaria: ponatur potestas binaria
proxime maior quam n, =2m, multiplicetur functio proposita per
2m-n factores simplices reales quoscunque. Ex resolubilitate producti
in factores reales secundi gradus, nullo negotio deriuatur, etiam functionem
propositam in factores reales secundi vel primi gradus resolubilem esse debere.
8.
Contra hanc demonstrationem obiici potest.
1. Regulam, secundum quam E. concludit, ex 2m-1 aequationibus
2m-2 incognitas α,β etc. λ, μ etc. omnes rationaliter
determinari posse, neutiquam esse generalem, sed saepissime exceptionem pati. Si
quis e. g. in art. 3, aliaque incognitarum tamquam cognita spectata,
reliquas per hanc et coefficientes datos rationaliter exprimere tentat, facile
inueniet, hoc esse impossibile, nullamque quantitatum incognitarum aliter quam
per aequationem m-1ti gradus determinari posse. Quamquam
vero hic statim a priori perspici potest, illud necessario ita euenire debuisse:
tamen merito dubitari posset, annon etiam in casu praesenti pro quibusdam
valoribus ipsius m res eodem modo se habebat; vt incognitae
α,β etc. λ, μ etc. ex u,B,C etc. aliter quam per
aequationem gradus forsan maioris quam 2m determinari nequeant. Pro eo
casu, vbi aequatio X=0 est quarti gradus, E. valores rationales
coëfficientium per u et coëfficientes datos eruit; idem vero etiam in
omnibus aequationibus altioribus fieri posse, vtique explicatione ampliori
egebat. – Ceterum operae pretium esse videtur, in formulas illas, quae α,
β etc. rationaliter per u, B, C etc. exprimant, profundius et
generalissime inquirere; de qua re aliisque ad eliminationis theoriam
(argumentum haudquaquam exhaustum) pertinentibus alia occasione fusius agere
suscipiam.
2. Etiamsi autem demonstratum fuerit, cuiusuis gradus sit aequatio
X=0, semper formulas inueniri posse, quae ipsas α, β etc.
λ, μ etc. rationaliter per u, B, C etc. exhibeant: tamen
certum est, pro valoribus quibusdam determinatis coëfficientium B, C
etc. formulas illas indeterminatas euadere posse, ita vt non solum
impossibile sit, incognitas illas rationaliter ex u, B, C etc.
definire, sed adeo reuera quibusdam in casibus valori alicui reali ipsius
u nulli valores reales ipsarum α, β etc. λ, μ etc.
respondeant. Ad confirmationem huius rei breuitatis gratia ablego lectorem ad
diss. ipsam E. vbi p. 236. aequatio quarti gradus fusius explicata est. Statim
quisque videbit, formulas pro coëfficientibus α, β indeterminatas
fieri, si C=0 et pro u assumatur valor 0, illorumque
valores non solum sine extractione radicum assignari non posse, sed adeo ne
reales quidem esse, si fuerit BB-4D quantitas negatiua. Quamquam vero
in hoc casu u adhuc alios valores reales habere, quibus valores reales
ipsarum α, β respondeant, facile perspici potest: tamen vereri aliquis
posset, ne huius difficultatis enodatio (quam E. omnino non attigit) in
aequationibus altioribus multo maiorem operam facessat. Certe haec res in
demonstratione exacta neutiquam silentio praeteriri debet.
3. Ill. E. supponit tacite, aequationem X=0 habere 2m
radices, harumque summam statuit =0 ideo quod terminus secundus in
X abest. Quomodo de hac licentia (qua omnes auctores de hoc argumento
vtuntur) sentiam, iam supra art. 3. declaraui. Propositio, summam omnium radicum
aequationis alicuius coëfficienti primo, mutato signo, aequalem esse, ad alias
aequationes applicanda non videtur, nisi quae radices habent: iam quum per hanc
ipsam demonstrationem euinci debeat, aequationem X=0 reuera radices
habere, haud permissum videtur, harum existentiam supponere. Sine dubio ii, qui
huius paralogismi fallaciam nondum penetrauerunt, respondebunt, hic non
demonstrari, aequationi X=0 satisfieri posse (nam hoc dicere vult
expressio, eam habere radices), sed tantummodo, ipsi per valores ipsios
x sub forma a+b√-1 contentos satisfieri posse; illud vero
tamquam axioma supponi. At quum aliae quantitatum formae, praeter realem et
imaginariam a+b√-1 concipi nequeant, non satis luculentum videtur,
quomodo id quod demonstrari debet ab eo, quod tamquam axioma supponitur,
differat; quin adeo si possibile esset adhuc alias formas quantitatum
excogitare, puta formam F, F′, F′′ etc. tamen sine demonstratione
admitti non deberet, cuius aequationi per aliquem valorem ipsius x aut
realem, aut sub forma a+b√-1, aut sub forma F, aut sub
F′ etc. contentum satisfieri posse. Quamobrem axioma illud alium sensum
habere nequit quam hunc: Cuius aequationi satisfieri potest aut per
valorem realem incognitae, aut per valorem imaginariam sub forma
a+b√-1 contentum, aut forsan per valorem sub forma alia hucusque
ignota contentum, aut per valorem, qui sub nulla omnino forma continetur.
Sed quomodo huiusmodi quantitates de quibus ne ideam quidem fingere potes –
vera vmbrae vmbra – summari aut multiplicari possint; hoc ea perspicuitate,
quae in mathesi semper postulatur, certo non intelligitur.*4)
Ceterum conclusiones, quas E. ex suppositione sua elicuit, per has
obiectiones haudquaquam suspectas reddere volo; quin potius certus sum, illas
per methodum neque difficilem neque ab Euleriana multum diuersam ita comprobari
posse, vt nemini vel minimus scrupulus superesse debeat. Solam formam
reprehendo, quae quamuis in inueniendis nouis veritatibus magnae
vtilitatis esse possit, tamen in demonstrando, coram publico, minime
probanda videtur.
4. Pro demonstratione assertionis, productum pqr etc. ex
coëfficientibus in X rationaliter determinari posse, ill. E.
nihil omnino attulit. Omnia, quae hac de re in aequationibus quarti
gradus explicat, haec sunt (vbi a, b, c, d sunt radices aequationes
propositae x4+Bxx+Cx+D=0):
«On m'objectera sans doute, que j'al supposé ici, que la quantité
pqr étoit une quantité réelle, et que son quarré ppqqrr étoit
affirmatif; ce qui étoit encor douteux, vu que les racines a, b, c, d
étant imaginaire, il pourroit bien arriver, que le quarré de la quantité
pqr, qui en es composée, fut negatif. Or je reponds à cela que ce cas
ne sauroit jamais avoir lieu; car quelque imaginaires que soient les racines
a,b,c,d, on sait pourtant, qu'il doit y avoir a+b+c+d=0;
ab+ac+ad+bc +bb+cd=B; abc+abd+acd+bcd=-C *5); abcd
=D, ces quantités B,C,D étant réelles. Mais puisque
p= a+b, q=a+c, r=a+b, leur produit pqr=(a+b)(a+c)a+d)
est determinable comme on sait, par les quantités B,C,D, et sera
par conseéquent réel, tout comme nous avons vu, qu'il est effectivement
pqr=-C, et ppqqrr=CC. On reconnoitra aisément de même, que
dans les plus hautes équations cette même circonstance doit avoir lieu, et qu'on
ne sauroit me faire des objections de ce coté.» Conditionem, productum
pqr etc. rationaliter per B,C etc. determinari posse,
E. nullibi adiecit, attamen semper subintellexisse videtur, quum absque illa
demonstratio nullam vim habere possit. Iam verum quidem est in aequationibus
quarti gradus, si productum (a+b)(a+c)(a+d) euoluatur obtineri
aa(a+b+c+d)+abc+abd+acd+bcd=-C, attamen non satis perspicuum videtur,
quomodo in omnibus aequationibus superioribus productum rationaliter per
coëfficientes determinari possit. Clar. de Foncenex, qui primus hoc obseruauit
(Miscell. phil. math. soc. Taurin. T. I. p. 117.), recte contendit, sine
demonstratione rigorosa huius propositionis methodum omnem vim perdere, illam
vero satis difficilem sibi videri confitetur, et quam viam frustra tentauerit,
enarrat. *6)
Attamen haec res haud difficulter per methodum sequentem (cuius summam
addigitare tantummodo hic possum) obsoluitur: Quamquam in aequationibus quarti
gradus non satis clarum est, productum (a+b)(a+c)(a+d) per
coëfficientes B,C,D determinabile esse, tamen facile perspici potest,
idem productum etiam esse = (b+a)(b+c)(b+d), nec non
=(c+a)(c+b)(c+d), denique etiam =(d+a)(d+b)(d+c). Quare
productum pqr erit quadrans summae
(a+b)(a+c)(a+d)+(b+a)(b+c)(b+d)+
(c+a)(c+b)(c+d)+(b+a)(b+d)(d+c), quam, si evoluatur, fore functionem
rationalem integram radicum a,b,c,d talem, in quam omnes eadem ratione
ingrediantur, nullo negotio a priori praeuideri potest. Tales vero functiones
semper rationaliter per coëfficientes aequationis, cuius radices sunt a, b,
c, d, exprimi possunt. – Idem etiam manifestum est, si productum
pqr sub hanc formam redigatur:
1/2 (a+b-c-d) x 1/2 (a+c-b-d) x 1/2
(a+d-b-c),
quod productum euolutum omnes a, b, c, d eodem modo implicaturum
esse facile praeuideri potest. Simul periti facile hinc colligent, quomodo hoc
ad altiores aequationes applicare debeat. – Completam demonstrationis
expositionem, quam hic apponere breuitas non permittit, vna cum vberiori
disquisitione de functionibus plures variabiles eodem modo inuoluentibus ad
aliam occasionem mihi reseruo.
Ceterum obseruo, praeter has quatuor obiectiones, adhuc quaedam alia in
demonstratione E. reprehendi posse, quae tamen silentio praetereo, ne forte
censor nimis seuerus esse videar, praesertim quum praecedentia satis ostendere
videatur, demonstrationem in ea quidem forma, in qua ab E. proposita est, pro
completa neutiquam haberi posse.
Post hanc demonstrationem, E. adhuc aliam viam theorema pro aequationibus,
quarum gradus non est potestas binaria, ad talium aequationum resolutionem
reducendi ostendit: attamen quum methodus haec pro aequationibus quarum gradus
est potestas binaria, nihil doceat, insuperque omnibus obiectionibus praecc.
(praeter quartam) aeque obnoxia sit vt demonstratio prima generalis: haud
necesse est illam hic fusius explicare.
9.
In eadem commentatione ill. E. theorema nostrum adhuc alia via confirmare
annixus est p. 263, cuius summa continetur in his: Proposita aequatione
xn+Axn-1+Bxn-2 etc. =0,
hucusque quidem expressio analytica, quae ipsius radices exprimat, inueniri non
potuit, si exponens n>4; attamen certum esse videtur (vti asserit
E.), illam nihil aliud continere posse, quam operationes arithmeticas et
extractiones radicum eo magis complicatas, quo maior sit n. Si hoc
conceditur, E. optime ostendit, quantumuis inter se complicata sint signa
radicalia, tamen formulae valorem semper per formam M+N√-1
repraesentabilem fore, ita vt M, N sint quantitates reales.
Contra hoc ratiocinium obiici potest, post tot tantorum geometrarum labores
perexiguam spem superesse, ad resolutionem generalem aequationum algebraicarum
vmquam perueniendi, ita vt magis magisque verisimile fiat, talem resolutionem
omnino esse impossibilem et contradictoriam. Hoc eo minus paradoxum videri
debet, quum id quod vulgo resolutio aequationis dicitur proprie nihil aliud
sit quam ipsius reductio ad aequationes puras. Nam aequationum purarum
solutio hinc non docetur sed supponitur, et si radicem aequationis
xm=H per m√H exprimis illam neutiquam
soluisti, neque plus fecisti, quam si ad denotandam radicem aequationis
xn+Axn-1+ etc. =0 signum aliquod
excogitares, radicemque huic aequalem poneres. Verum est, aequationes puras
propter facilitatem ipsarum radices per approximationem inueniendi, et propter
nexum elegantem, quem omnes radices inter se habent, prae omnibus reliquis
multum praestare, adeoque neutiquam vituperandum esse, quod analystae harum
radices per signum peculiare denotauerunt: attamen ex eo, quod hoc signum
perinde vt signa arithmetica additionis, subtractionis, multiplicationis,
diuisionis et euectionis ad dignitatem sub nomine expressionum
analyticarum complexi sunt, minime sequitur cuiusuis aequationis radicem per
illas exhibere posse. Seu, missis verbis, sine ratione sufficienti supponitur,
cuiusuis aequationis solutionem ad solutionem aequationum purarum reduci posse.
Forsan non ita difficile foret, impossibilitatem iam pro quinto gradu omni
rigore demonstrare, de qua re alio loco disquisitiones meas fusius proponam. Hic
sufficit, resolubilitatem generalem aequationum in illo sensu acceptam, adhuc
valde dubiam esse, adeoque demonstrationem, cuius tota vis ab illa suppositione
pendet, in praesenti rei statu nihil ponderis habere.
10.
Postea etiam clar. de Foncenex, quum in demonstratione prima Euleri defectum
animaduertisset (supra art. 8. obiect. 4.), quem tollere non poterat, adhuc
aliam viam tentauit et in comment. laudata p. 120. in medium protulit *7). Quae consistit
in sequentibus.
Proposita sit aequatio Z=0, designante Z functionem
mti gradus incognitae z. Si m est numerus
impar, iam constat, aequationem hanc habere radicem realem; si vero m
est par, clar. F. sequenti modo probare conatur, aequationem ad minimum vnam
radicem formae p+q√-1 habere. Sit m=2ni, designante
i numerum imparem, supponaturque zz+uz+M esse diuisor
functionis Z. Tunc singuli valores ipsius u erunt summae
binarum radicum aequationis Z=0 (mutato signo), quamobrem u
habebit (m . m-t) / (1 . 2)=m′ valores, et si u per
aequationem U=0 determinari supponitur (designante U
functionem integram ipsius u et coëfficientium cognitorum in
Z), haec erit gradus m′ti. Facile vero perspicitur
m′ fore numerum formae 2n-1i′, designante
i′ numerum imparem. Iam nisi m′ est impar, supponatur iterum,
uu+uu′+M′ esse diuisorem ipsius U, patetque per similia
ratiocinia u′ determinari per aequationem U′=0, vbi
U′ sit functio (m′ . m′-1) / (1 . 2)ti gradus ipsius
u′. Posito vero (m′ . m′-1) / (1 . 2)=m′′, erit m′′
numerus formae 2n-2i′′, designante i′′ numerum
imparem. Iam nisi m′′ est impar, statuatur u′ u′+u′′u′+M′′
esse diuisorem functionis U′, determinabiturque u′′ per
aequationem U′′=0, quae si supponitur esse gradus
m′′′ti, m′′′ erit numerus formae
sn-3i′′′. Manifestum est, in serie aequationum U=0,
U′=0, U′′=0 etc. ntam fore gradus imparis
adeoque radicem realem habere. Statuemus breuitatis gratia n=3, ita vt
aequatio U′′=0 radicem realem u′′ habeat, nullo enim negotio
perspicitur pro quouis alio valore ipsius n idem ratiocinium valere.
Tunc coëfficientem M′′ per u′′ et coëfficientes in U′
(quos fore functiones integras coëfficientium in Z facile
intelligitur), siue per u′′ et coëfficientes in Z rationaliter
determinabilem fore asserit clar. de F., et proin realem. Hinc sequitur, radices
aequationis u′ u′+u′′u′+M′′=0 sub forma p+q√-1 contentas fore;
eadem vero manifesto aequationi U′=0 satisfacient: quare dabitur valor
aliquis ipsius u′ sub forma p+q√-1 contentus. Iam coëfficiens
M′ (eodem modo vt ante) rationaliter per u′ et coëfficientes
in Z determinari potest, adeoque etiam sub forma p+q√-1
contentus erit; quare aequationis uu+u′ u+M′ radices sub eadem forma
contentae erunt, simul vero aequationi U=0 satisfacient, i. e.
aequatio haec habebit radicem sub forma p+q√-1 contentam. Denique
hinc simili ratione sequitur, etiam M sub eadem forma contineri, nec
non radicem aequationis zz+uz+M=0, quae manifesto etiam aequationi
propositae Z=0 satisfaciet. Quamobrem quaeuis aequatio ad minimum vnam
radicem formae p+q√-1 habebit.
11.
Obiectiones 1, 2, 3, quas contra Euleri demonstrationem primam feci (art.
8.), eandem vim contra hanc methodum habent, ea tamen differentia, vt obiectio
secunda, cui Euleri demonstratio tantummodo in quibusdam casibus specialibus
obnoxia erat, praesentem in omnibus casibus attingere debeat. Scilicet a priori
demonstrari potest, etiamsi formula detur, quae coëfficientem M′
rationaliter per u′ et coëfficientes in Z exprimat, hanc pro
pluribus valoribus ipsius u′ necessario indeterminatam fieri debere;
similiterque formulam, quae coëfficientem M′′ per u′′
exhibeat, indeterminatam fieri pro quibusdam valoribus ipsius u′′ etc.
Hoc luculentissime perspicietur, si aequationem quarti gradus pro exemplo
assumimus. Ponamus itaque m=4, sintque radices aequationis
Z=0, hae α, β, γ, δ. Tum patet aequationem U=0 fore
sexti gradus ipsiusque radices -(α+β), -(α+γ),
-(α+δ), -(β+γ), -(β+δ), -(γ+δ). Aequatio
U′=0 autem erit decimi quinti gradus, et valores ipsius u′ hi
2α+β+γ, 2α+β+δ, 2α+γ+δ, 2β+α+γ,
2β+α+δ, 2β+γ+δ, 2γ+α+β, 2γ+α+δ,
2γ+β+δ, 2δ+α+β, 2δ+α+γ, 2δ+β+γ,
α+β+γ+δ, α+β+γ+δ, α+β+γ+δ. Iam in hac aequatione,
quippe cuius gradus est impar, subsistendum erit, habebitque ea reuera radicem
realem α+β+γ+δ (quae primo coëfficienti in Z mutato signo
aequalis adeoque non modo realis sed etiam rationalis erit, si coëfficientes in
Z sunt rationales). Sed nullo negotio perspici potest, si formula
detur, quae valorem ipsius M′ per valorem respondentem ipsius
u′ rationaliter exhibeat, hanc necessario pro u′=α+β+γ+δ
indeterminatam fieri. Hic enim valor ter erit radix aequationis
U′=0, respondebuntque ipsi tres valores ipsius M′, puta
(α+β)(γ+δ), (α+γ)(β+δ) et (α+δ)(β+γ), qui omnes
irrationales esse possunt. Manifesto autem formula rationalis neque valorem
irrationalem ipsius M′ in hoc casu producere posset, neque tres valores
diuersos. Ex hoc specimine satis colligi potest, methodum clar. de Foncenexii
neutiquam esse satisfacientem, sed si ab omni parte completa reddi debeat, multo
profundius in theoriam eliminationis inquiri oportere.
12.
Denique ill. LaGrange de theoremate nostro egit in comm. Sur la forme des
racines imaginaires des equations, Nouv. Mem. de l' Acad. de Berlin 1772. p. 222
sqq. Magnus hic geometra imprimis operam dedit, defectus in Euleri
demonstratione prima supplere et reuera praesertim ea, quae supra (art. 8.)
obiectionem tertiam et quartam constituunt, tam profunde perscrutatus est, vt
nihil amplius desiderandum restet, nisi forsan in disquisitione anteriori supra
theoria eliminationis (cui inuestigatio haec tota innititur) quaedam dubia
superesse videantur. – Attamen obiectionem primam omnino non attigit, quin
etiam tota disquisitio superstructa est suppositioni, quamuis aequationem
mti gradus reuera m radices habere.
Probe itaque iis, quae hucusque exposita sunt, perpensis, demonstrationem
nouam theorematis grauissimi ex principiis omnino diuersis petitam peritis haud
ingratam fore spero, quam exponere statim aggredior.
13.
LEMMA. Denotante m numerum integrum positiuum quemcunque, functio sin
φ. xm-sin mφ. rm-1x+sin(m-1)φ. rm
diuisibilis erit per xx-2cos φ. rx+rr.
Demonstr. Pro m=1 functio illa sit =0 adeoque per
quemcunque factorem diuisibilis; pro m=2 quotiens sit sin φ,
et pro quouis valore maiori quotiens erit sin φ. xm-2+sin 2φ.
rxm-3 +sin3φ. rrxm-4+ etc. +sin(m-1)φ.
rm-2. Facile enim confirmatur multiplicata hac functione per
xx-2cosφ. rx+rr, productum functioni propositae aequale fieri.
14.
LEMMA. Si quantitas r angulusque φ ita sunt determinati, vt
habeantur aequationes
rm cos mφ+Arm-1
cos(m-1)φ+Brm-2 cos(m-2)φ+ etc.
+Krrcos2φ+Lrcosφ+M=0 [1]
rm sin
mφ+Arm-1 sin(m-1)φ+Brm-2 sin(m-2)φ+ etc.
+Krrsin2φ+Lrsinφ=0 [2]
functio
xm+Axm-1+Bxm-2+ etc.
+Kxx+Lx+M=X diuisibilis erit per factorem duplicem xx-2cosφ.
rx+rr, si modo r. sinφ non =0; si vero r.
sinφ=0, eadem functio diuisibilis erit per factorem simplicem
x-rcosφ.
Demonstr. I. Ex art. praec. omnes sequentes quantitates diuisibiles
erunt per xx-2cosφ. rx+rr:
| sinφ. rxm |
- |
sin mφ. rmx |
+ |
sin(m-1)φ. rm+1 |
| Asinφ. rxm-1 |
- |
Asin(m-1)φ. rm-1 |
+ |
Asin(m-2)φ. rm |
| Bsinφ. rxm-2 |
- |
Bsin(m-2)φ. rm-2 |
+ |
Bsin(m-2)φ. rm-1 |
| |
etc. |
|
|
etc. |
| Ksinφ. rxx |
- |
Ksin2φ. rxx |
+ |
Ksinφ. r3 |
| Lsinφ. rx |
- |
Lsinφ. rx |
|
* |
| Msinφ. r |
|
* |
+ |
Msin(-φ)r. |
Quamobrem etiam summa harum quantitatum per xx-2cosφ. rx+rr
diuisibilis erit. At singularum partes primae constituunt summam sinφ.
rX; secundae additae dant 0, propter [2]; tertiarum vero
aggregatum quoque euanescere, facile perspicitur, si [1] multiplicatur per
sinφ, [2] per cosφ, productumque illud ab hoc subducitur. Vnde
sequitur, functionem sinφ. rX diuisibilem esse per xx-2cosφ.
rx+rr, adeoque, nisi fuerit rsinφ=0, etiam functionem X.
Q. E. P.
II. Si vero rsinφ=0, erit aut r=0 aut sinφ=0. In
casu priori erit M=0, propter [1], adeoque X per x
siue per x-rcosφ diuisibilis; in posteriori erit cosφ=±1,
cos2φ= +1, cos3φ=±1 et generaliter cos
nφ=cosφn. Quare propter [1] fiet X=0, statuendo
x=cosφ, et proin functio X per x-cosφ erit
diuisibilis. Q. E. S.
15.
Theorema praecedens plerumque adiumento quantitatum imaginariarum
demonstratur, vid. Euler Introd. in Anal. Inf. T. I. p. 110; operae
pretium esse duxi, ostendere, quomodo aeque facile absque illarum auxilio erui
possit. Manifestum iam est, ad demonstrationem theorematis nostri nihil aliud
requiriri quam vt ostendatur: Proposita functione quacunque X formae
xm+Axm-1+ Bxm-2+ etc.+Lx+M,
r et φ ita determinari posse, vt aequationes [1] et
[2] locum habeant. Hinc enim sequetur, X habere factorem
realem primi vel secundi gradus; diuisio autem necessario producet quotientem
realem inferioris gradus, qui ex eadem ratione quoque factorem primi vel secundi
gradus habebit. Per continuationem huius operationis X tandem in
factores reales simplices vel duplices resoluetur. Illud itaque theorema
demonstrare, propositum est sequentium disquisitionum.
16.
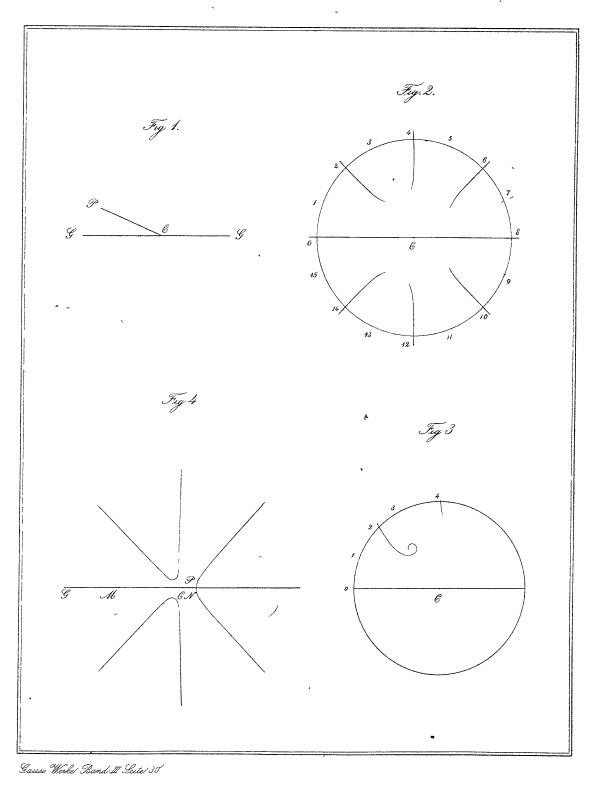
Concipiatur planum fixum infinitum (planum tabulae, fig. 1.), et in hoc recta
fixa infinita GC per punctum fixum C transiens. Assumta aliqua
longitudine pro vnitate vt omnes rectae per numeros exprimi possint, erigatur in
quouis puncto plani P, cuius distantia a centro C est
r angulusque GCP=φ, perpendiculum aequale valori expressionis
rmsin mφ+Arm-1sin(m-1)φ+ etc.+Lrsinφ,
quem breuitatis gratia in sequentibus semper per T designabo.
Distantiam r semper tamquam positiuam considero, et pro punctis, quae
axi ab altera parte iacent, angulus φ aut tamquam duobus rectis maior,
aut tamquam negatiuus (quod hic eodem redit) spectari debet. Extremitates horum
perpendiculorum (quae pro valore positiuo ipsius T supra planum
accipiendae sunt, pro negatiuo infra, pro euanescente in plano ipsio) erunt ad
superficiem curuam continuam quaquauersum infinitam, quam breuitatis gratia in
sequentibus superficiem primam vocabo. Prorsus simili modo ad idem planum
et centrum eundemque axem referatur alia superficies, cuius altitudo supra
quoduis plani punctum sit rmcos
mφ+Arm-1cos(m-1)φ+ etc. +Lrcosφ+M, quam expressionem
breuitatis gratia semper per U denotabo. Superficiem vero hanc, quae
etiam continua et quaquauersum infinita erit, per denominationem superficiei
secundae a priori distinguam. Tunc manifestum est, totum negotium in eo
versari, vt demonstretur, ad minimum vnum punctum dari, quod simul in plano, in
superficie prima et in superficie secunda iaceat.
17.
Facile perspici potest, superficiem primam partim supra planum partim infra
planum iacere; patet enim distantiam a centro r tam magnam accipi
posse, vt reliqui termini in T prae primo rmsin mφ
euanescant; hic vero, angulo φ rite determinato, tam positiuus quam
negatiuus fieri potest. Quare planum fixum necessario a superficie prima
secabitur; hanc plani cum superficie prima intersectionem vocabo lineam
primam; quae itaque determinabitur per aequationem T=0. Ex eadem
ratione planum a superficie secunda secabitur; intersectio constituet curuam per
aequationem U=0 determinatam, quam lineam secundam appellabo.
Proprie vtraque curua ex pluribus ramis constabit, qui omnino seiuncti esse
possunt, singuli vero erunt lineae continuae. Quin adeo linea prima semper erit
talis, quam complexam vocant, axisque GC tamquam pars huius curuae
spectanda; quicunque enim valor ipsi r tribuatur, U semper
fiet =0, quando φ aut =0 aut =180°. Sed
praestat complexum cunctorum ramorum per omnia puncta, vbi T=0,
transeuntium tamquam vnam curuam considerare (secundum vsum in geometria
sublimiori generaliter receptum), similiterque cunctos ramos per omnia puncta
transeuntes, vbi U=0. Patet iam, rem eo reductam esse, vt demonstretur,
ad minimum vnum punctum in plano dari, vbi ramus aliquis lineae primae a ramo
lineae secundae secetur. Ad hunc finem indolem harum linearum propius
contemplari oportebit.
18.
Ante omnia obseruo, vtramque curuam esse algebraicam, et quidem, si ad
coordinates orthogonales reuocetur, ordinis mti. Sumto enim
initio abscissarum in C, abscissisque x versus G,
applicatis y versus P, erit x=rcosφ,
y=rsinφ, adeoque generaliter, quidquid sit n,
rnsin nφ=nxn-1y-(n. n-1. n-2) / (1. 2. 3)
xn-3y3 +(n. .. n-4) / (1. .. .5)
xn-5y5- etc., rncos
nφ=xn-(n. n-1) / (1. 2) xn-2yy +(n. n-1. n-2.
n-3) / (1. 2. 3. 4) xn-4y4- etc. Quamobrem tum
T tum U constabunt ex pluribus huiusmodi terminis
axα yβ, denotantibus α, β
numeros integros positiuos, quorum summa, vbi maxima est, sit =m.
Ceterum facile praeuideri potest, cunctos terminos ipsius T factorem
y inuoluere, adeoque lineam primam proprie ex recta (cuius aequatio
y=0) et curua ordinis m-1ti compositam esse; sed
necesse non est ad hanc distinctionem hic respicere.
Maioris momenti erit inuestigatio, an linea prima et secunda crura infinita
habeant, et quot qualiaque. In distantia infinita a puncto C linea
prima, cuius aequatio sin mφ+1/r sin(m-1)φ +B/rr sin(m-2)φ etc.
=0, confundetur cum linea, cuius aequatio sin mφ=0. Haec vero
exhibet m lineas rectas in puncto A se secantes, quarum prima
est axis GCG′, reliquae contra hanc sub angulis 1/m 180,
2/m 180, 3/m 180 etc. graduum inclinatae. Quare linea prima
2m ramos infinitos habet, qui peripheram circuli radio infinito
descripti in 2m partes aequales dispertiuntur, ita vt peripheria a ramo
primo secetur in concursu circuli et axis, a secundo in distantia 1/m
180°, a tertio in distantia 2/m 180° etc. Eodem modo linea secunda
in distantia infinita a centro habebit asymptotam per aequationem cos
mφ=0 expressam, quae est complexus m rectarum in puncto C
sub aequalibus angulis itidem se secantium, ita tamen, vt prima cum axi
CG constituat angulum 1/m 90°, secunda angulum 3/m
90°, tertia angulum 5/m 90° etc. Quare linea secunda etiam
2m ramos infinitos habebit, quorum singuli medium locum inter binos
ramos proximos linea primae occupabunt, ita vt peripheriam circuli radio
infinite magno descripti in punctis, quae 1/m 90°, 3/m 90°,
5/m 90° etc. ab axe distant, secent. Ceterum palam est, axem ipsum
semper duos ramos infinitos lineae primae constituere, puta primum et
m+1tum. Luculentissime hic ramorum situs exhibetur in fig. 2, pro casu m=4 constructa, vbi rami lineae secundae, vt a ramis lineae
primae distinguantur, punctati exprimuntur, quod etiam de figura quarta est
tenendum. *8) –
Quum vero hae conclusiones maximi momenti sint, quantitatesque infinite magnae
quosdam lectores offendere possint: illas etiam absque infinitorum subsidio in
art. sequ. eruere docebo.
19.
THEOREMA. Manentibus cunctis vt supra, ex centro C describi
poterit circulos, in cuius peripheria sint 2m puncta, in quibus
T=0, totidemque, in quibus U=0, et quidem ita, vt singula
posteriora inter bina priorum iaceant.
Sit summa omnium coëfficientium A,B etc. K,L,M, positiue
acceptorum =S, accipiaturque R simul >S√2 et
>1 *9): tum dico in
circulo radio R descripto ea, quae in theoremate enunciata sunt,
necessario locum habere. Scilicet designato breuitatis gratia eo puncto huius
circumferentiae, quod 1/m 45 gradibus ab ipsius concursu cum laeua
parte axis distat, siue pro quo φ= 1/m 45°, per (1); similiter
eo puncto, quod φ=3/m 45°, ab hoc concursu distat, siue pro quo
φ=3/m 45°, per (3); porro eo, vbi φ=5/m 45°, per (5) etc.
vsque ad (8m-1), quod (8m-1)/m 45 gradibus ab illo concursu
distat, si semper versus eandem partem progrederis, (aut 1/m 45° a
parte opposita), ita vt omnino 4m puncta in peripheria habeantur,
aequalibus interuallis dissita: iacebit inter (8m-1) et (1) vnum
punctum, pro quo T=0; nec non sita erunt similia puncta singula inter
(3) et (5); inter (7) et (9); inter (11) et (13) etc. quorum itaque multitudo
2m; eodemque modo singula puncta, pro quibus U=0, iacebunt
inter (1) et (3); inter (5) et (7); inter (9) et (11), quorum multitudo igitur
etiam =2m; denique praeter haec 4m puncta alia, in tota
peripheria non dabuntur, pro quibus vel T vel U sit
=0.
Demonstr. I. In puncto (1) erit mφ=45° adeoque T=
Rm-1(R√1/2 +Asin(m-1)φ+B/R sin(m-2)φ+ etc. +
L/(Rm-2) sinφ); summa vero Asin(m-1)φ+B/R sin(m-2)φ
etc. certo non poterit esse maior quam S, adeoque necessario erit minor
quam R√1/2: vnde sequitur in hoc puncto valorem ipsius T certo
esse positiuum. A potiori itaque T valorem positiuum habebit, quando
mφ inter 45° et 135° iacet, i. e. a puncto (1)
vsque ad (3) valor ipsius T semper positiuus erit. Ex eadem ratione
T a puncto (9) vsque ad (11) positiuum valorem vbique habebit, et
generaliter a quouis puncto (8k+1) vsque ad (8k+3), denotante
k integrum quemcunque. Simili modo T vbique inter (5) et (7),
inter (13) et (15) etc. et generaliter inter (8k+5) et (8k+7a)
valorem negatiuum habebit, adeoque in omnibus his interuallis nullibi poterit
esse =0. Sed quoniam in (3) hic valor est positiuus, in (5) negatiuus:
necessario alicubi inter (3) et (5) erit =0; nec non alicubi inter (7)
et (9); inter (11) et (13) etc. vsque ad interuallum inter (8m-1) et
(1) incl., ita vt omnino in 2m punctis habeatur T=0. Q. E.
P.
II. Quod vero praeter haec 2m puncta, alia, hac proprietate
praedita, non dantur, ita cognoscitur. Quum inter (1) et (3); inter (5) et (7)
etc. nulla sint, aliter fieri non posset, vt plura talia puncta exstent, quam si
in aliquo interuallo inter (3) et (5), vel inter (7) et (9) etc. ad minimum duo
iacerent. Tum vero nesessario in eodem interuallo T alicubi esset
maximum, vel minimum, adeoque (dT)/(dφ)=0. Sed
(dT)/(dφ)=mRm-2(Rcos mφ+(m-1)/m Acos(m-1)φ+ etc.) et cos
mφ inter (3) et (5) semper est negatiuus et >√1/2. Vnde facile
perspicitur in toto hoc interuallo (dT)/(dφ) esse quantitatem
negatiuam; eodemque modo inter (7) et (9) vbique positiuam; inter (11) et (13)
negatiuam etc. ita vt in nullo horum interuallorum esse possit 0, adeoque
suppositio consistere nequeat. Quare etc. Q. E. S.
III. Prorsus simili modo demonstratur, U habere valorem negatiuum
vbique inter (3) et (5), inter (11) et (13) etc. et generaliter inter
(8k+3) et (8k+5); positiuum vero inter (7) et (9), inter
(15) et (17) etc. et generaliter inter (8k+7) et (8k+9). Hinc
statim sequitur, U=0 fieri debere alicubi inter (1) et (3), inter (5)
et (7) etc., i. e. in 2m punctis. In nullo vero horum
interuallorum fieri poterit (dT)/(dφ)=0 (quod facile simili modo vt
supra probatur): quamobrem plura quam illa 2m puncta in circuli
peripheria non dabuntur, in quibus fiat U=0. Q. E. T. et Q.
Ceterum ea theorematis pars, secundum quam plura quam 2m puncta non
dantur, in quibus T=0, neque plura quam 2m, in quibus
U=0, etiam inde demonstrari potest, quod per aequationes T=0,
U=0 exhibentur curuae mti ordinis, quales a circulo
tamquam curuae secundi ordinis in pluribus quam 2m punctis secari non
posse, ex geometria sublimiori constat.
20.
Si circulus alius radio maiori quam R ex eodem centro describitur,
eodemque modo diuiditur: etiam in hoc inter puncta (3) et (5) iacebit punctum
vnum, in quo T=0, itemque inter (7) et (9) etc., perspicieturque
facile, quo minus radius huius circuli a radio R differat, eo propius
huiusmodi puncta inter (3) et (5) in vtriusque circumferentia sita esse debere.
Idem etiam locum habebit, si circulus radio aliquantum minori quam R,
attamen maiori quam S√2 et 1 describitur. Ex his nullo negotio
intelligitur, circuli radio R descripti circumferentiam in eo puncto
inter (3) et (5), vbi T=0, reuera secari ab aliquo ramo lineae
primae; idemque valet de reliquis punctis, vbi T=0. Eodem modo patet,
circumferentiam circuli huius in omnibus 2m punctis, vbi U=0,
ab aliquo ramo lineae secundae secari. Hae conclusiones etiam sequenti modo
exprimi possunt: Descripto circulo debitae magnitudinis e centro C, in
hunc intrabunt 2m rami lineae primae totidemque rami lineae secundae,
et quidem ita, vt bini rami proximi lineae primae per aliquem ramum lineae
secundae ab inuicem separentur. Vid. fig. 2, vbi circulus iam non infinitae sed
finitae magnitudinis erit, numerique singulis ramis adscripti cum numeris, per
quos in art. praec. et hoc limites certos in peripheria breuitatis caussa
designaui, non sunt confundendi.
21.
Iam ex hoc situ relatiuo ramorum in circulum intrantium tot modis diuersis
deduci potest, intersectionem alicuius rami lineae primae cum ramo lineae
secundae intra circulum necessario dari, vt quaenam potissimum methodus prae
reliquis eligenda sit, propemodum nesciam. Luculentissima videtur esse haec:
Designemus (fig. 2.) punctum peripheriae circuli, vbi a laeua axis parte (quae
ipsa est vnus ex 2m ramis lineae primae) secatur, per 0; punctum
proximum, vbi ramus lineae secundae intrat, per 1; punctum huic proximum, vbi
secundus lineae primae ramus intrat, per 2, et sic porro vsque ad 4m-1,
ita vt in quouis puncto numero pari signato ramus lineae secundae in circulum
intret, contra ramus lineae secundae in omnibus punctis per numerum imparem
expressis. Iam ex geometria sublimori constat, quamuis curuam algebraicam, (siue
singulas cuiusuis curuae algebraicae partes, si forte e pluribus composita sit)
aut in se redientem aut vtrimque in infinitum excurrentem esse, adeoque si ramus
aliquis curuae algebraicae in spatium definitum intret, eundem necessario ex hoc
spatio rursus alicubi exire debere. *10) Hinc
concluditur facile, quoduis punctum numero pari signatum (seu, breuitatis
caussa, quoduis punctum par) per ramum lineae primae cum alio puncto pari
intra circulum iunctum esse debere, similiterque quoduis punctum numero impari
notatum cum alio simili puncto per ramum lineae secundae. Quamquam vero haec
binorum punctorum connexio secundum indolem functionis X perquam
diuersa esse potest, ita vt in genere determinari nequeat, tamen facile
demonstrari potest, quaecunque demum illa sit, semper intersectionem lineae
primae cum linea secunda oriri.
22.
Demonstratio huius necessitatis commodissime apagogice repraesentari posse
videtur. Scilicet supponamus, iunctionem binorum quorumque punctorum parium, et
binorum quorumque punctorum imparium ita adornari posse, vt nulla intersectio
rami lineae primae cum ramo lineae secundae inde oriatur. Quoniam axis est pars
lineae primae, manifesto punctum 0 cum puncto 2m iunctum erit. Punctum
1 itaque cum nullo puncto vltra axem sito, i. e. cum nullo puncto per numerum
maiorem quam 2m expresso iunctum esse potest, alioquin enim linea
iungens necessario axem secaret. Si itaque 1 cum puncto n iunctum esse
supponitur, erit n<2m. Ex simili ratione si 2 cum n′
iunctum esse statuitur, erit n′<n, quia alioquin ramus 2 ...
n′ ramum 1 ... n necessario secaret. Ex eadem caussa punctum 3 cum
aliquo punctorum inter 4 et n′ iacentium iunctum erit, patetque si
3,4,5 etc. iuncta esse supponantur cum n′′, n′′′, n′′′′ etc.,
n′′′ iacere inter 5 et n′′, n′′′′ inter 6 et n′′′
etc. Vnde perspicuum est, tandem ad aliquod punctum h peruentum iri,
quod cum puncto h+2 iunctum sit, et tum ramus, qui in puncto
h+1 in circulum intrat, necessario ramum puncta h et
h+2 iungentem secabit. Quia autem alter horum duorum ramorum ad lineam
primam, alter ad secundam pertinebit, manifestum iam est, suppositionem esse
contradictoriam, adeoque necessario alicubi intersectionem lineae primae cum
linea secunda fieri.
Si haec cum praecedentibus iunguntur, ex omnibus disquisitionibus explicatis
colligetur, theorema, quamuis functionem algebraicam rationalem integram
vnius indeterminatae in factores reales primi vel secundi gradus resolui
posse, omni rigore esse demonstratum.
23.
Ceterum haud difficile ex iisdem principiis deduci potest, non solum vnam sed
ad minimum m intersectiones lineae primae cum secunda dari, quamquam
etiam fieri potest, vt linea prima a pluribus ramis lineae secundae in eodem
puncto secetur, in quo casu functio X plures factores aequales habebit.
Attamen quum hic sufficiat, vnius intersectionis necessitatem demonstrauisse,
fusius huic rei breuitatis caussa non immoror. Ex eadem ratione etiam alias
harum linearum proprietates hic vberius non persequor, e. g.
intersectionem semper fieri sub angulis rectis; aut si plura crura vtriusque
curuae in eodem puncto conueniant, totidem crura lineae primae affore, quot
crura lineae secundae, haecque alternatim posita esse, et sub aequalibus angulis
se secare etc.
Denique obseruo, minime impossibile esse, vt demonstratio praecedens, quam
hic principiis geometricis superstruxi, etiam in forma mere analytica
exhibeatur: sed eam repraesentationem, quam hic explicaui, minus abstractam
euadere credidi, verumque neruum probandi hic multo clarius ob oculos poni, quam
a demonstratione analytica exspectari possit.
Coronidis loco adhuc aliam methodum theorema nostrum demonstrandi addigitabo,
quae primo aspectu non modo a demonstratione praecedente, sed etiam ab omnibus
demonstrationibus reliquis supra enarratis maxime diuersa esse videbitur, et
quae nihilominus cum d'Alembertiana, si ad essentiam spectas, proprie eadem est.
Cum qua illam comparare, parallelismumque inter vtramque explorare peritis
committo, in quorum gratiam vnice subiuncta est.
24.
Supra planum figurae 4. relatiue ad axem CG punctumque fixum
C descriptas suppono superficiem primam et secundam eodem modo vt
supra. Accipe punctum quodcunque in aliquo ramo lineae primae situm siue vbi
T=0, ( e. g. quodlibet punctum M in axe iacens), et
nisi in hoc etiam U=0, progredere ex hoc puncto in linea prima versus
eam partem, versus quam magnitudo absoluta ipsius U decrescit. Si forte
in puncto M valor absolutus ipsius U versus vtramque partem
decrescit, arbitrarium est, quorsum progrediaris; quid vero faciendum sit, si
U versus vtramque partem crescat, statim docebo. Manifestum est itaque,
dum semper in linea prima progrediaris, necessario tandem te ad punctum
peruenturum, vbi U=0, aut ad tale, vbi valor ipsius U fiat
minimum, e. g. punctum N. In priori casu quod quaerebatur inuentum est;
in posteriori vero demonstrari potest, in hoc puncto plures ramos lineae primae
sese intersecare (et quidem multitudinem parem ramorum), quorum semissis ita
comparati sint, vt si in aliquem eorum deflectas (siue huc siue illuc) valor
ipsius U adhucdum decrescere pergat. (Demonstrationem huius
theorematis, prolixiorem quam difficiliorem breuitatis gratia supprimere debeo.)
In hoc itaque ramo iterum progredi poteris, donec U aut fiat
=0 (vti in fig. 4. euenit in P), aut denuo minimum. Tum rursus
deflectes, necessarioque tandem ad punctum peruenies, vbi sit U=0.
Contra hanc demonstrationem obiici posset dubium, annon possibile sit, vt
quantumuis longe progrediaris, et quamuis valor ipsius U semper
decrescat, tamen haec decrementa continuo tardiora fiant, et nihilominus ille
valor limitem aliquem nusquam attingat; quae obiectio responderet quartae in
art. 6. Sed haud difficile foret, terminum aliquem assignare, quem simulac
transieris, valor ipsius U necessario non modo semper rapidius mutari
debeat, sed etiam decrescere non amplius possit, ita vt antequam ad hunc
terminum perueneris, necessario valor 0 etiam affuisse debeat. Hoc vero et
reliqua, quae in hac demonstratione addigitare tantummodo potui, alia occasione
fusius exsequi mihi reseruo.
E r r a t a. Pag. 7. annot. lin. 5. pro imaginarium
l. imaginariam. p. 13. l. vlt. pro 23. l. 24. p. 14. l. 17. pro
2-1, l. 2m-1. p. 15. l. 4. por vnum l. vnam. p.
16. l. 12. pro multiplicetur, l. multipliceturque. ibid. l. 21. pro
aliaque, l. aliqua. p. 28. l. 7 et 8. pro cosφ, l.
rcosφ.
*1) Sub quantitate imaginaria hic semper intelligo quantitatem in forma
a+b√-1 contentam, quamdiu b non est =0. In hoc sensu
expressio illa semper ab omnibus geometris primae notae accepta est, neque
audiendos censeo, qui quantitatem a+b√-1 in eo solo casu imaginarium
vocare voluerunt vbi a=0, impossibilem vero quando non sit
a=0, quum haec distinctio neque necessaria sit neque vllius vtilitatis.
– Si quantitates imaginariae omnino in analysi retineri debent (quod pluribus
rationibus consultius videtur, quam ipsas abolere, modo satis solide
stabiliantur): necessario tamquam aeque possibiles ac reales spectandae sunt;
quamobrem reales et imaginarias sub denominatione communi quantitatum
possibilium complecti mallem: contra, impossibilem dicerem
quantitatem, quae conditionibus satisfacere debeat, quibus ne imaginariis quidem
concessis satisfieri potest, attamen ita, vt phrasis haec idem significet
ac si dicas, talem quantitatem in toto magnitudinum ambitu non dari. Hinc vero
genus peculiare quantitatum formare, neutiquam concederem. Quodsi quis dicat,
triangulum rectilineum aequilaterum rectangulum impossibile esse, nemo erit qui
neget. At si tale triangulum impossibile tamquam nouum triangulorum genus
contemplari, aliasque triangulorum proprietates ad illud applicare voluerit,
ecquis risum teneat? Hoc esset verbis ludere seu potius abuti. – Quamuis vero
etiam summi mathematici saepius veritates, quae quantitatum ad quas spectant
possibilitatem manifesto supponunt, ad tales quoque applicauerint quarum
possibilitas adhuc dubia erat; neque abnuerim, huiusmodi licentias plerumque ad
solam formam et quasi velamen rationiorum pertinere, quod veri geometrae acies
mox penetrare possit: tamen consultius, scientiaeque, quae tamquam
perfectissimum claritatis et certitudinis exemplar merito celebratur,
sublimitate magis dignum videtur, tales libertates aut omnino proscribere, aut
saltem parcius neque alias ipsis vti, nisi vbi etiam minus exercitati perspicere
valeant, rem etiam absque illarum subsidio etsi forsan minus breuiter tamen
aeque rigorose absolui potuisse. – Ceterum haud negauerim, ea quae hic contra
impossibilium abusum dixi, quodam respectu etiam contra imaginarias obiici
posse: sed harum vindicationem nec non totius huius rei expositionem vberiorem
ad aliam occasionem mihi reseruo.
*2) Obseruare conuenit, ill. d'Alembert in sua huius demonstrationis
expositione considerationes geometricas adhibuisse, atque X tamquam
abscissam, x tamquam ordinatam curuae spectauisse (secundum morem
omnium geometrarum primae huius saeculi partis, apud quos notio functionum minus
usitata erat). Quia vero omnia ipsius ratiocinia, si ad ipsorum essentiam solam
respicis, nullis principiis geometricis, sed pure analyticis innituntur, et
curua imaginaria, ordinataeque imaginariae expressiones duriores esse
lectoremque hodiernum facilius offendere posse videntur, formam
repraesentationis mere analyticam hic adhibere malui. Hanc annotationem ideo
adieci, ne quis demonstrationem d'Alembertianam ipsam cum hac succinta
expositione comparans aliquid essentiale immutatum esse suspicetur.
*3) Hacce occasione obiter adnoto, ex harum serierum numero plurimas esse,
quae primo aspectu maxime conuergentes videantur, e. g. ad maximam partem
eas, quibus ill. Euler in parte poster. Inst. Calc. Diff. Cap. VI. ad summam
aliarum serierum quam proxime assignandam vtitur p. 441–474. (reliquae enim
series p. 475–478 reuera conuergere possunt), quod, quantum scio, a nemine
hucusque obseruatum est. Quocirca magnopere optandum esset, vt dilucide et
rigorose ostenderetur, cur huiusmodi series, quae primo citissime, dein
paullatim lentius lentiusque conuergunt, tandemque magis magisque diuergunt,
nihilominus summam proxime veram suppeditent, si modo non mimis multi termini
capiantur, et quousque talis summa pro exacta tuto haberi possit?
*4) Tota haec res multum illustrabitur per aliam disquisitionem sub prelo iam
sudantem vbi in argumento longe quidem diuerso, nihilominus tamen analogo,
liceutiam similem prorsus eodem iure vsurpare potuissem, vt hic in aequationibus
ab omnibus analystis factum est. Quamquam vero plurium veritatum demonstrationes
adiumento talium fictionum paucis verbis absoluere licuisset, quae absque his
perquam difficiles euadunt et subtilissima artificia requirunt, tamen illis
omnino abstinere malui, speroque, paucis me satisfacturum fuisse, si analystarum
methodum imitatus essem.
*5) E. per errorem habet C, vnde etiam postea perperam statuit
pqr=C.
*6) In hanc expositionem error irrepsisse videtur, scilicet p. 118. l. 5.
loco characteris v (on choissoit seulement celles où entroit p
etc. ), necessario legere oportet, une même racine quelconque de l'équation
proposée, aut simile quid, quum illud nullum sensum habeat.
*7) In tomo secundo eorundem Miscellaneorum p. 337. dilucidationes ad hanc
commentationem continentur: attamen hae ad disquisitionem praesentam non
pertinent, sed ad logarithmos quantitatum negatiuarum, de quibus in eadem comm.
sermo fuerat.
*8) Figura quarta constructa est supponendo
X=x4-2xx+3x+10, in qua itaque lectores disquisitionibus
generalibus et abstractis minus assueti situm respectiuum vtriusque curuae in
concreto intueri poterunt. Longitudo lineae CG assumta est
=10.
*9) Quando S>√1/2, conditio prima secundam; quando vero
S<√1/2 secunda primam implicabit.
*10) Satis bene certe demonstratum esse videtur, curuam algebraicam neque
alicubi subito abrumpi posse (vti e. g. euenit in curua transscendente, cuius
aequatio y=1/log x), neque post spiras infinitas in aliquo puncto se
quasi perdere (vt spiralis logarithmica), quantumque scio nemo dubium contra rem
mouit. Attamen si quis postulat, demonstrationem nullis dubiis obnoxiam alia
occasione tradere suscipiam. In casu praesenti vero manifestum est, si aliquis
ramus e. g. 2, ex circulo nullibi exiret (fig. 3.), te in circulum inter 0 et 2
intrare, postea circa totum hunc ramum (qui in circuli spatio se perdere
deberet) circummeare, et tandem inter 2 et 4 rursus ex circulo egredi posse, ita
vt nullibi in tota via in lineam primam incideris. Hoc vero absurdum esse inde
patet, quod in puncto, vbi in circulum ingressus es, superficiem primam supra te
habuisti, in egressu, infra; quare necessario alicubi in superficiem primam
ipsam incidere debuisti, siue in punctum lineae primae. – Ceterum ex hoc
ratiocinio principiis geometriae situs innixo, quae haud minus valida sunt, quam
principia geometriae magnitudinis, sequitur tantummodo, si in aliquo ramo lineae
primae in circulum intres, te alio loco ex circulo rursus egredi posse, semper
in linea prima manando, neque vero, viam tuam esse lineam continuam in eo sensu,
quo in geometria sublimori accipitur. Sed hic sufficit, viam esse lineam
continuam in sensu communi, i. e. nullibi interruptam sed vbique cohaerentem.
|
|