Ludi Romani

_________________________________________________________

Ludus latrunculorum

Tabula ludi

De lusionis ratione.

Uterque lusor vicenos calculos eiusdem coloris habet. His utrimque abaci ordines exteriores occupantur bini. At non in areolis ponuntur, sed in ipsis decussationibus linearum longitrorsus et transverse ductarum, quibus tramitibus calculi moventur.

Initialis calculorum dispositio.

De lusus processu.

Uter ludere incipiat, inter lusores convenit vel sorte consulta decer­nitur. Porro post primam lusus vicem is, qui victus est, prior incipit. Uterque autem lusor alternatim calculum promovendo tractum ducit. Quos calculos licet ut turrim in scaciludio – in omnes partes promovere, id est: ante, retro, laevorsum, dextrorsum usque ad obstaculum alicuius calculi. Tamen calculus ante proprium lusoris calculum aut ante ad­versarii calculum positus in linearum decussationem proximam tran­silire potest, quae res graphice demonstratur.

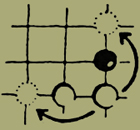
Saltus calculi albi.

Id autem studendum est, ut quam plurimi calculi alterius tollantur, id est: caedantur.

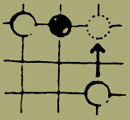
Caeditur calculus niger albo calculo.

Hoc fit ea ratione in lusibus veteribus usitata, ut lusor calculum adversarii ex duabus decussationibus ex adversum sitis coangustet. Quod cum fit, fieri potest, ut duo aut tres uno tractu calculi adversarii caedantur.

Calculus caesus de abaco seponendus eius est quasi captivus, qui cecidit ipsum. Nihil tamen sequitur, si calculus inter duos adversarii calculos ponitur, in quorum altero latere sive alii calculi adversarii sunt sive nulli.

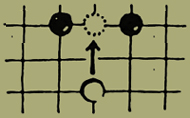
Calculus albus promovetur, sed sine periculo.

In lusus initio uterque lusor id studere potest, ut suos calculos post adversarii calculos promotos ponat et collocet, ut in illos ex obliquo incurset. Quae cum fiunt, adversarius id studebit, ut calcuIos in discrimen adductos aut seducat aut aliis calculis adductis tutetur. Talibus tutationum conaminibus fieri potest, ut calculi ita conglobati impediantur, quominus in incursationem faciendam expediri possint. Itaque interdum fit, ut adversarius effugere non iam possit. Nam tractu sollerti duo aut tres calculi adversarii ita circumdantur, ut vix unus eorum protegi possit.

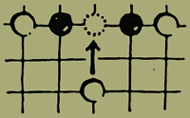
Duo calculi negri caedantur calculi albi tractu.

Calculi iuxta positi.

Duo calculi negri caedantur calculi albi tractu.

Calculi angulatim positi.

Quomodo lusus finiatur.

Lusus finitur, si alteruter lusor omnes adversarii calculos cepit. Si vero ambo lusores pariter sollertes pariterque attenti congrediuntur, fieri potest, ut tales obsidiones efficiantur, cum ordines calculorum plus minusve constipati utriusque lusoris ita dispositi sint, ut quilibet cal­culus promotus ab adversario caedatur et capiatur. Talis quotiescumque condicio est, lusus finitur, isque est victor, qui plures adversarii calculos cepit. Tamen talis lusus etiam continuari potest, si alteruter lusor opina­tur calculo quodam proprio perutiliter perdendo suam condicionem in melius mutari posse.

Porro potest fieri, ut in fine lusus ambo lusores paucos calculos in abaco positos habeant numero vix differentes – velut quinos et quinos aut quinque et septem – quibus fieri non iam poterit, ut alteruter adversarii calculos caedat. Talis cum est status, ex consensu utriusque lusoris lusus finiri potest. Is autem tum est victor, qui plures calculos cepit. Sed si ambo totidem numero calculos ceperunt, non est victoria, sed exitus dubius.

Est ergo ad lusum latrunculorum sollertia necessaria, cum attentio summa sit adhibenda. qualis facultas rem acriter observandi ludendo excolitur. Itaque fieri potest, ut lusores latrunculorum eodem fere modo ad strategemata excogitanda incitentur quo scacorum lusores.

Translatio latina:

P. C. Eichenseer, Universitas Saarbrücken

Textus originalis germanicus:

Gudrun Eger